Kapasitet på jernbane
__NUMBEREDHEADINGS__
Kapasitetsbegrepet
Avgrensning
Først skal vi gjøre en avgrensing siden kapasitetsbegrepet brukes i mange sammenhenger.
Ordet kapasitet betyr egentlig evne til å romme/yte. I vår sammenheng kan vi kanskje si at kapasitet betyr evne til å transportere.
Også innen jernbane-virksomhet omtaler man kapasitet i mange ulike forbindelser. Man kan snakke om et togs kapasitet (antall passasjerer eller tonnasje som toget kan “romme”), en skiftestasjons kapasitet (antall vogner den kan behandle pr. tidsenhet) og en enkelt streknings eller et helt nettverks kapasitet (hva strekningen/nettverket evner å transportere). Sistnevnte kan uttrykkes som antall tog pr. tidsenhet, passasjerer pr. tidsenhet (nærtrafikk, T-bane), vogner pr. tidsenhet (baner som overveiende transporterer gods) eller tonn pr. tidsenhet (f.eks. malmbaner). I dette dokumentet skal vi konsentrere oss om kapasiteten av en enkelt strekning og det i form av antall tog pr. tidsenhet.
Kapasiteten på en strekning avhenger ikke bare av strekningens utforming, men også av egenskapene til de togene som skal trafikkere den. Videre har rekkefølgen av ulike togslag (“ruteplanen”) stor betydning for kapasiteten. Dette skal vi se tydelig i kap. 2. Man kan altså endre en streknings kapasitet uten å endre noe ved selve strekningen. Det kan også anslås en kapasitet uten kjennskap til togenes rekkefølge ved å anta alle muligheter som like sannsynlige, men i det følgende vil vi holde oss til metoder basert på ruteplaner.
Teoretisk og praktisk kapasitet
Begrepsmessig skiller man ofte mellom den teoretiske (maksimale) kapasitet og den praktisk nyttbare kapasitet.
Når det gjelder den teoretiske kapasitet, tenker man seg at de aktuelle togslag i den aktuelle rekkefølge kjøres så tett som signalsystemet tillater, men likevel slik at togene kan kjøre med full hastighet. I dette ligger det altså ingen marginer som kan fange opp forsinkelser slik at nesten enhver forsinkelse vil forplante seg til flere (i verste fall alle) andre tog. En strekning kan vanskelig drives med en slik trafikkmengde i praksis, derav betegnelsen teoretisk og maksimal kapasitet.
I begrepet praktisk kapasitet trekkes det inn at transporten må skje med en viss kvalitet, i denne sammenheng særlig i form av punktlighet. Det må altså være mindre enn et visst maksimum av forsinkelser (eller forstyrrelser for å bruke et mer generelt ord) for at vi skal kunne si at vi opererer innenfor en gitt kapasitet. Når forsinkelser stadig er uakseptabelt store, er det et tegn på at man overskrider strekningens (praktiske) kapasitet. Vi vil derfor sette opp følgende generelle definisjon av den praktisk nyttbare kapasitet:
Kapasiteten av en strekning er evnen til å fremføre tog med en akseptabel punktlighet.
Denne definisjonen er ikke-operasjonell og inneholder et element av skjønn i og med uttrykket “akseptabel”. Den praktisk nyttbare kapasitet er således ikke et skarpt definert begrep. Dette vil bli noe nærmere omtalt og illustrert i kap. 5.3.2.
Man kan belaste en strekning ut over den praktiske kapasitet, men ikke ut over den teoretiske kapasitet (uten å øke kjøretider, bryte sikkerhetsbestemmelser o.l., altså bryte noen av forutsetningene kapasiteten er beregnet på grunnlag av).
Uttrykket forsinkelser må presiseres som tilleggs-forsinkelser påført på den aktuelle strekning, altså sekundære forsinkelser (dvs. forsinkelser som skyldes andre togs forsinkelser). Forsinkelser fra utgangsstasjonen, forsinkelser pga. uhell etc. sier selvsagt ikke noe om en streknings kapasitet. Men i hvor stor grad slike primære forsinkelser sprer seg til andre tog sier noe om strekningens kapasitet.
Det som vi her har omtalt som den teoretiske kapasitet kan oftest tallfestes forholdsvis eksakt. Dette skal vi vise metoder for i de følgende kapitler. For å få et tall for den praktiske kapasitet må man inkludere skjønnsmessige anslag; som oftest uttrykt i form av hvor stor del av den teoretiske kapasitet man kan utnytte. For grundigere studier vil bruk av simuleringsmodeller ofte være aktuelt.
Oversikt over innholdet
Vi tar først opp kapasitet på dobbeltspor fordi dette er lettest å framstille, og fordi det fins enkle formler som gir en god indikasjon på kapasiteten. Mesteparten av arbeidet med beregning av kapasiteten ved slike formler går med til å finne av de såkalte togfølgetidene. I kap. 2 forutsettes derfor at disse er kjent for å få introdusert det viktigste på en lettfattelig måte. I kap. 3 tar vi opp beregning av togfølgetider og noe mer om kapasitetsforhold på dobbeltspor.
For kapasitetsberegninger på enkeltsporede strekninger er de formlene man kan bruke, noe mer kompliserte og neppe så representative som ved anvendelse på dobbeltspor. Behandlingen av enkeltspor i kap. 4 er derfor noe enklere enn behandlingen av dobbeltspor. Viktige tiltak for kapasitetsøkning er også omtalt siden dette ofte er den mest aktuelle problemstillingen for enkeltspor.
Mye av framstillingen i disse kapitlene bygger på ref. / 1 /, / 2 / og / 3 /. Det første er et UIC-dokument som beskriver en metode for å anslå kapasitet i antall tog pr. tidsenhet. Fordi den er beskrevet i dokument 405E omtales den også som UIC 405E. Dokumentet er skrevet på tysk og er noe tungt tilgjengelig. Derimot er ref. / 2 / og / 3 / mye enklere å tilegne seg og er skrevet på engelsk. De omhandler britiske forhold med størst vekt på togfølgetid og 4-begrep signalsystem. Fremstillingen i kap. 2-4 er vesentlig enklere enn i ref. / 1 /, og det er lagt vekt på de faktorer som er aktuelle for norske forhold.
I kap. 5 gis en analytisk beskrivelse av forplantning av forsinkelser for enkle skjematiske situasjoner. Ulike typer feilsituasjoner og deres konsekvenser for strekningens kapasitet. omtales også.
Til slutt gis det - i kap. 6 - en kort innføring i bruk av simuleringsmodeller til å studere kapasitetsforhold på jernbanestrekninger. Fremstillingen sikter mot brukere av simuleringsmodeller - ikke mot dem som skal konstruere en modell.
Kapasitet på dobbeltspor, gitt togfølgetider
Vi ser her på kapasiteten av ett spor med all trafikk i samme retning.
Mesteparten av kapitlet omhandler beregning av den teoretiske kapasitet. Praktisk kapasitet omtales i et eget avsnitt. Alle relative forhold (endringer i kapasitet pga. ulike faktorer) som omtales er imidlertid like gyldige enten man ser på den teoretiske eller den praktiske kapasitet.
Med minste togfølgetid (engelsk “headway”) menes den minste tidsavstanden som kan opprettholdes mellom to tog slik at det andre toget på betryggende måte kan kjøre med maksimal hastighet. Eller noe annerledes uttrykt: den minste tidsavstanden hvor det andre toget kan kjøre uhindret av det første. Denne tidsavstanden må regnes mellom samme punkt (vanligvis fronten) på begge togene. I det følgende vil ofte bare togfølgetid bli brukt selv om det menes minste togfølgetid.
I dette kapitlet fortsettes stort sett at togfølgetidene er kjent. I neste kapittel går vi nærmere inn på beregning av togfølgetider.
For mesteparten av dette kapitlet gjør vi følgende forutsetninger og forenklinger for strekningen vi ser på:
- Det er ikke avgreninger eller separate forbikjøringsspor underveis
- Sporforbindelser mellom de to sporene til bruk ved enkeltsporet drift og andre unormale situasjoner regnes ikke som forbikjøringsspor
- Alle togene trafikkerer hele strekningen
Ensartet trafikk
Vi ser først på det enkleste tilfellet hvor alle togene er (tilnærmet) like og framføres med samme hastighet og stoppmønster.
Dette er typisk for spesielle dobbeltsporstrekninger som T-baner og strekninger med bare én trafikktype (dette er uvanlig i norsk nett). Dette kan forekomme i perioder på på 4-spors strekninger som rundt Oslo hvor f.eks. passasjertog har identiske ruteplaner.
Den minste togfølgetiden vil da være den samme mellom alle togene, og den påvirkes ikke av togenes kjøretid fordi alle togene har samme kjøretid. Den teoretiske maksimalkapasiteten K i et tidsrom T er da ganske enkelt
der t er den minste togfølgetiden mellom togene av den aktuelle type.
Beregning av togfølgetider kommer vi tilbake til i neste kapittel, men vi skal her bare foregripe med en enkel beregning for å finne den hastighet som gir maksimal kapasitet.
Vi ser da på en strekning uten stopp hvor togene har konstant hastighet v over hele strekningen. Det foregår altså ingen akselerasjon eller retardasjon noe sted på strekningen. Videre forutsetter vi 3-begrep signalering med blokklengde b.
Togenes lengde kalles L, og det antas at bremsing innledes en avstand ts·v før et restriktivt signal. Togfølgetiden kan da uttrykkes (fullstendig utledning er gitt i kap. 3.3):
Strekningskapasiteten blir da
I dette enkle tilfelle skal vi finne den optimale hastighet, i betydningen den hastighet som gir maksimal kapasitet. Det må da forutsettes en sammenheng mellom blokklengde og hastighet; blokklengden settes i prinsippet lik bremselengden, men i praksis vil det alltid være en noe uspesifikk påplussing som kan være konstant eller hastighetavhengig. For denne beregningen vil vi velge et konstant tillegg s. Ved konstant retardasjon r blir blokklengden da
Ved innsetting for b i uttrykket for K får vi
Ved derivasjon av K m.h.p. v får vi
Følgelig er den optimale hastighet gitt ved
Eksempel: Vi skal anslå den optimale hastigheten for en strekning med ensartet trafikk av typiske nærtrafikktog. Vi bruker da verdiene L = 200 m, r = 1 m/s2, og skjønnsmessig setter vi s til 100 m. Dette gir
Den optimal hastighet blir følgelig 20 m/s (72 km/h).
Den tilhørende maksimale kapasitet per tidsenhet blir (med 10 sekunders siktavstand)
Den tilhørende blokklengden er
Vi minner om at det selv med denne korte blokklengden bare er forutsatt 3-aspekt signalering.
Som det fremgår av det ovenstående er det flere valg som er gjort i denne utledningen; dette gjelder uttrykkene for siktavstand (her valgt proporsjonal med hastigheten; størrelsen faller da bort ved utledning av den optimale hastighet) og uttrykket for blokklengde. Alternative måter å uttrykke disse på gir varierende optimal hastighet, men i alle tilfelle blir den optimale hastighet så lav at den som oftest vil være markedsmessig helt uinteressant.
Vi skal likevel nevne et tilfelle (forekommer ikke i Norge) hvor en slik optimal hastighet kan være interessant. Det gjelder en situasjon hvor to sterkt trafikkerte dobbeltspor har en kort felles strekning uten stopp. For å slippe en utvidelse til 4 spor kan det da være et alternativ å signalere en slik kort strekning for maksimal kapasitet selv om det betyr redusert hastighet. Som det fremgår av eksempelet blir da den teoretiske maksimalkapasiteten på ca. 70 tog/time for hvert spor! Selv om dette stort sett må betraktes som en kuriositet, nevnes det likevel for å vise hvor høyt opp i kapasitet man kan komme under slike helt spesielle forhold.
I praksis vil man således nesten alltid drive en dobbeltsporstrekning med en hastighet godt over den hastighet som er optimal med hensyn på kapasitet. Av uttrykket for den deriverte av kapasitet m.h.p hastighet ser vi at i dette normale hastighetsområdet (over den optimale hastighet) synker kapasiteten med økende hastighet. Dette skyldes at bremselengden normalt er proporsjonal med kvadratet av hastigheten. Ved vesentlig hastighetsmessig oppgradering av et dobbeltspor vil man altså normalt få lavere kapasitet.
Konsekvensen av å innføre et stopp på en slik strekning skal vi se på i kap. 3 under beregning av togfølgetider.
Blandet trafikk
Dette er situasjonen på Bane NORs dobbeltspor og den typiske situasjonen for et dobbeltspor generelt.
Generelt
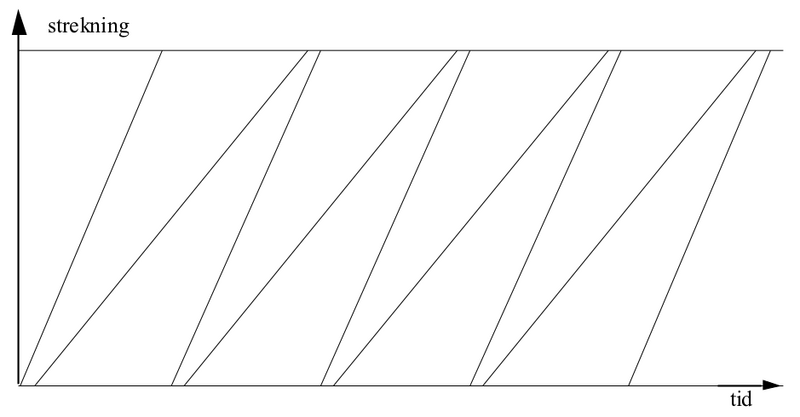
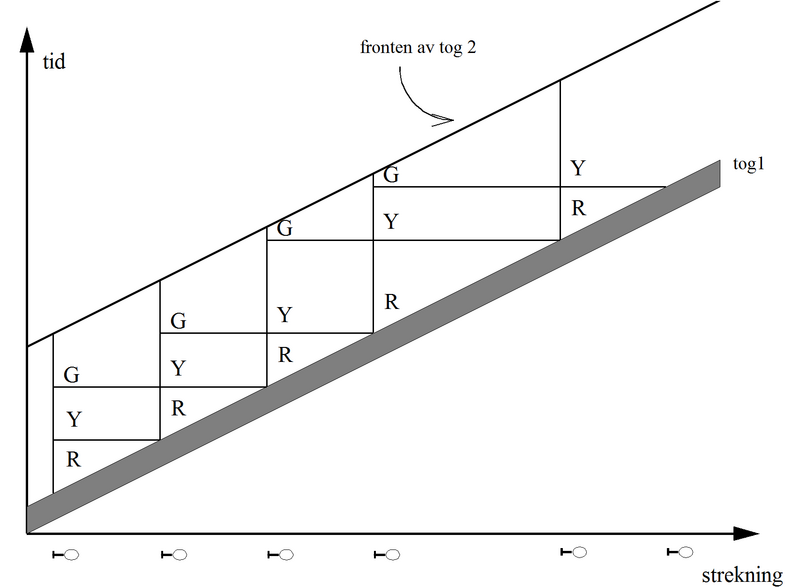
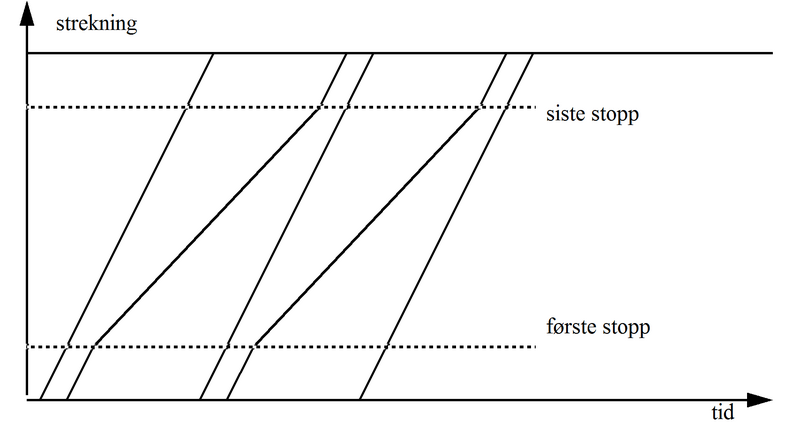
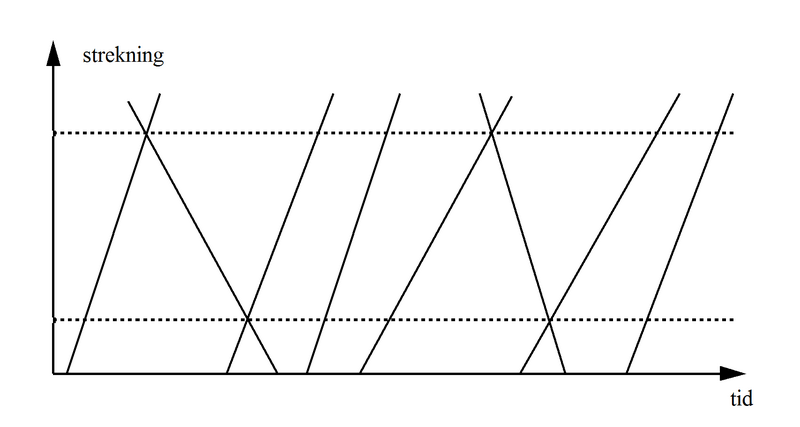
Med blandet trafikk blir kapasiteten vesentlig lavere enn ved ensartet trafikk. Dette kan man lett forstå kvalitativt bare ved å se på et tid-veg-diagram (grafisk rute) for de to situasjonene. Et typisk eksempel med langsomme og raske tog annenhver gang er vist nedenfor.
Figur 1: Grafisk rute (tid-veg diagram) ved maksimalt blandet trafikk
Et raskt tog (representert ved de sterkest stigende linjene på figuren) vil kjøre fra et langsommere, og det blir en stor tidsluke ved ankomst til ende-stasjonen. Tilsvarende må et raskt tog starte langt bak et langsomt tog for å kunne kjøre uhindret. Den signalmessige minste togfølgetid blir bare utnyttet over en liten del av strekningen, og det er lange tidsrom hvor sporet ikke kan benyttes. Dette gir selvsagt plass til vesentlig færre tog enn ved ensartet trafikk, og kapasiteten blir vesentlig lavere.
I denne situasjonen vil tidsavstanden mellom to ulike tog variere over strekningen. Togfølgetiden vi skal bruke i kapasitetsberegningen, må da bety den minste tidsavstanden mellom to tog et fast sted på strekningen forutsatt at det andre toget kan kjøre uhindret over hele strekningen. Det er ofte praktisk å benytte strekningens begynnelse som det punkt togfølgetidene refererer til. I denne situasjonen kommer altså togenes kjøretider med i togfølgetiden, i tillegg til den tidsavstand mellom togene som kommer fra signalene Den tidsavstand mellom togene som kan holdes på et gitt sted på strekningen, vil vi kalle den signalmessige minste togfølgetid. Togfølgetiden for et langsomt tog etter et raskt vil da i hovedsak bli bestemt av signaleringen ut fra utgangsstasjonen (samt hastighetsforhold her og togenes akselerasjon). Denne togfølgetiden kaller vi t som før. Togfølgetiden for et raskt tog etter et langsomt vil være minst ved ankomst til endestasjonen, og det er signaleringen her (samt hastighetsforhold og togenes retardasjon) som bestemmer den signalmessige minste togfølgetid i dette tilfellet. Men togfølgetiden ved utgangsstasjonen vil bestå av denne signalmessige togfølgetiden samt differansen i kjøretid mellom de to togene (se figuren ovenfor).
For den tallmessige beregning deler vi togene inn i klasser eller grupper med like eller tilnærmet like egenskaper.Typiske grupperinger er stoppende persontog, direkte persontog, godstog. Det trengs nå togfølgetider for alle de kombinasjoner av togfølger som finnes i ruteplanen. Man trenger ikke en fullstendig ruteplan, men man må ha rekkefølgen av tog fra de ulike grupperinger. Man teller opp antall tilfeller av de ulike kombinasjoner og beregner en midlere togfølgetid:
Her betyr
nij : antall togfølgetilfeller hvor et tog fra gruppe j kommer etter et fra gruppe i
tij : minste togfølgetid for et tog fra gruppe j etter et fra gruppe i
Summen tas over alle kombinasjoner av i og j. Opptellingen av tilfeller gjøres for et tidsrom av tilstrekkelig lengde til å få med alle aktuelle situasjoner.
Deretter beregnes den teoretiske kapasiteten som før:
To tog-grupper
Som oftest vil man bare ha to eller tre tog-grupper. Vi skal se nærmere på tilfellet med to grupper, f.eks. stoppende og direkte persontog. Dette er typisk for Bane NORs dobbeltsporstrekninger i rushtiden. For enkelhets skyld lar vi det her være like mange tog i de to gruppene. Den generelle situasjonen behandles i kap. 3.6.3.
Markedsmessig er det for mange togtyper ønskelig at de kjører med fast frekvens (stiv ruteplan). Dette medfører at man får stoppende og direkte tog annenhver gang, som på foregående figur. Videre forutsetter vi her at den signalmessige minste togfølgetid t er den samme over hele strekningen.
Differansen i kjøretid mellom tog fra de to gruppene (kalles her for Δt) er den variabelen som betyr mest for kapasiteten i slike situasjoner.
Togfølgetiden for et stoppende tog etter et direkte blir da t, og for den motsatte situasjonen blir togfølgetiden t + Δt. Siden vi her forutsetter at begge situasjonene forekommer like ofte, blir den midlere togfølgetid
Den teoretiske kapasiteten blir da
Vi ser straks at blandet trafikk gir en drastisk lavere kapasitet enn ensartet trafikk siden differansen i kjøretid mellom ulike togtyper (Δt) normalt er mye større enn den signalmessige togfølgetiden t. Av samme grunn innser vi at differansen i kjøretid er den parameteren som betyr mest for kapasiteten. Vi skal nå se et tallmessig eksempel på dette.
Eksempel: Vi skal anslå den teoretiske maksimalkapasiteten for en dobbeltsporstrekning med stoppende og direkte tog annenhver gang. Vi vil bruke typiske tallverdier for Bane NORs forstadsstrekninger (Oslo - Lillestrøm / Ski / Asker).
På Bane NORs dobbeltsporstrekninger varierer den minste togfølgetiden i området 1.5 - 4 min. Vi vil her bruke t = 2 min. som er en aktuell verdi for strekninger med tett signalering. Kjøretiden for stoppende tog over de nevnte strekningene ligger i området 26 - 33 min. For direkte tog har vi tilsvarende 18 - 24 min. Som en typisk verdi for differansen i kjøretid vil vi her bruke Δt = 10 min. (effektive nærtrafikktog taper knappe 1 min. pr. stopp, og strekningene har 11 - 12 stopp).
Tallverdiene ovenfor gir en teoretisk kapasitet på
[tog/time]
Som kontrast ville ensartet trafikk gitt en teoretisk kapasitet på 30 tog/time ved samme togfølgetid!
En dramatisk forbedring av den signalmessige minste togfølgetid fra 2 til 1 min. har i denne situasjon liten innvirkning på kapasiteten; den øker bare til K = 60 / (1 + 10/2) = 10 [tog/time]. Tilsvarende effekt ville kunne oppnås ved 2 minutters reduksjon av kjøretidsdifferansen, Δt: K = 60 / (2 + 8/2) = 10 [tog/time].
Ved høy frekvens for den stoppende togtypen (15 minutters intervall er ofte ønskelig i rushtidene), får man behov for å kjøre 8 tog pr. time (eller flere, da det ofte vil være behov for mer enn 4 direkte tog pr. time siden disse dekker mange ulike destinasjoner). Man får da en kapasitetsutnyttelse som ligger altfor nær den teoretiske maksimalkapasitet, og punktligheten blir dårlig.
Et vanlig “triks” når man får for høy kapasitetsutnyttelse ved blandet trafikk, er å øke kjøretiden for de direkte togene. Den rutemessige kjøretiden blir altså vesentlig større enn den teknisk mulige kjøretiden. Kjøretidsdifferansen blir da mindre og kapasiteten høyere. Dette er mye benyttet på Bane NORs forstadsstrekninger.
Slike kunstig forlengede kjøretider for de raskeste togene er et typisk tegn på manglende strekningskapasitet.
Hvis man i en slik situasjon isteden prøver å øke kjøretiden for de langsomme togene, kan man komme ille ut å kjøre, fordi kapasiteten da vil bli redusert pga. den økte kjøretidsdifferansen. Hvis kjøretiden for de langsomme togene økes (for å prøve å bedre punktligheten eller pga. langsommere materiell), må kjøretiden for alle de raske togene økes like mye hvis kapasiteten ikke skal reduseres. I en situasjon med anstrengt kapasitet vil det således være viktig å holde forholdsvis stramme ruter for de langsomme togene.
Redusert kjøretid for de langsomme togene vil av samme grunn være et meget effektivt tiltak for å øke kapasiteten.
Ruteplanens innvirkning på kapasiteten
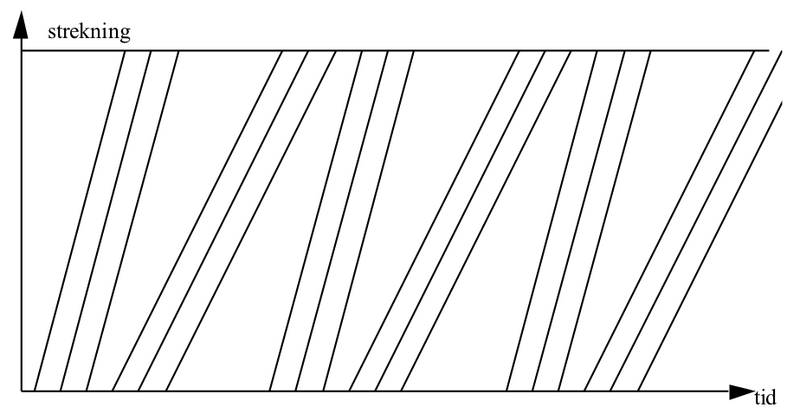
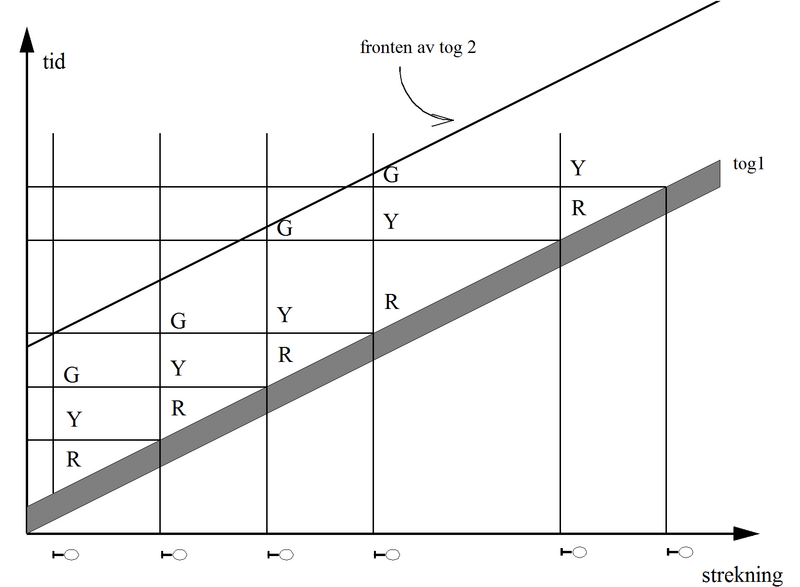
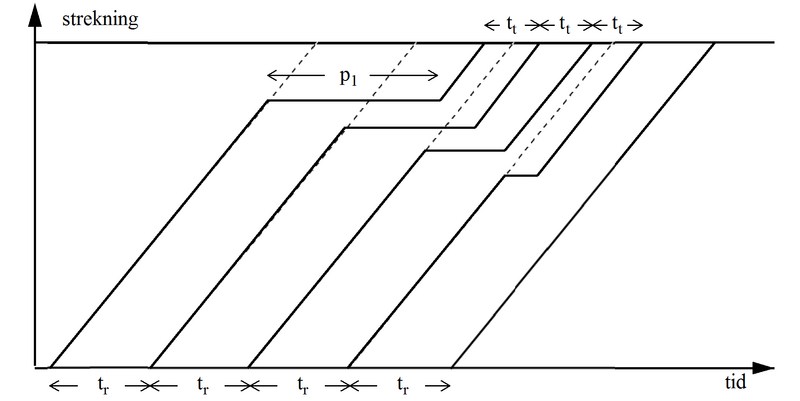
Vi skal så se litt på ruteplanens effekt på kapasiteten. Det tilfellet vi nå har sett mye på, er den situasjonen som gir lavest kapasitet. Straks man har mulighet til å kjøre to like tog etter hverandre, øker kapasiteten fordi man da får flere tilfeller med den minste togfølgetiden. Hvis vi vekselvis kjører n tog fra hver gruppe (figuren nedenfor viser n = 3), blir det 2n-1 tilfeller med den minste togfølgetid t for hvert tilfelle med togfølgetid t + Δt.
Figur 2: Grafisk rute (tid-veg diagram) med 3 tog i hver pulje
Den midlere togfølgetid blir da
Den teoretisk kapasiteten blir
Ved små n vil kapasiteten øke raskt med n, særlig i den vanlige situasjonen hvor Δt er betydelig større enn t.
En slik samling av like tog kalles puljekjøring, “batching” eller “flighting”. I praksis vil en slik ruteplan ofte være markedsmessig ugunstig og av den grunn ikke gjennomførbar. Men der hvor dette er mulig å gjennomføre, er det et effektivt tiltak for å øke kapasiteten.
Vi har nå sett mye på situasjonen med bare to tog-grupper. Ved flere enn to tog-grupper bør man på samme måte tilstrebe å ha færrest mulig tilfeller med et av de raskeste togene rett etter et av de langsomste. I hovedsak blir konklusjonene og resultatene for flere tog-grupper av samme type som for to selv om tallverdiene selvsagt blir noe forskjellig.
Som vi har sett flere eksempler på i det foregående, vil det ofte være en konflikt mellom markedsmessige krav til fast frekvens (stive ruter) og korte kjøretider på den ene siden og kravet til kapasitet på den andre siden. Pga. kapasitetens betydning for punktligheten, kan man si at dette til syvende og sist blir en avveining mellom ulike markedsmessige forhold.
Eksempel på beregning av teoretisk kapasitet
Vi vil her ta for oss et større eksempel med flere tog-grupper og ulike togfølgetider. Vi skal beregne den teoretiske kapasiteten i maksimaltimen i ettermiddags-rushet i retning fra Oslo til Lillestrøm. De rutedata som er benyttet er hentet fra ruteordningen for 1992/93 med noen ubetydelige endringer.
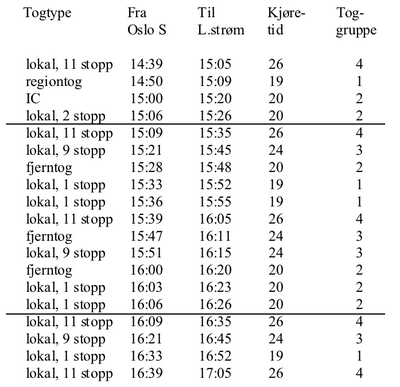
Først setter vi opp en liste (“rute”) over alle togene i rush-tiden:
Vi skal beregne kapasiteten i maksimaltimen, og av tabellen ovenfor ser man at denne strekker seg fra 15:06 til 16:03, alternativt fra 15:09 til 16:06. Det er likegyldig hvilket alternativ man velger, og her bruker vi det sistnevnte som er markert med de to linjene i listen ovenfor.
Ovenfor har vi også inndelt togene i fire grupper etter kjøretid. Vi setter så opp en tabell med antallet (n) av hver kombinasjon av togfølger slik som vist i det følgende. I samme tabell er de minste togfølgetidene (t) også angitt. Minste togfølgetid refererer utgangsstasjonen (Oslo S) og består av den signalmessige minste togfølgetid pluss eventuell differanse i kjøretid. Den minste togfølgetid på strekningene Oslo S - Bryn og Strømmen - Lillestrøm er ca. 3 min. For å få med ulike minste togfølgetider i dette eksempelet har vi her satt den minste togfølgetiden ut fra Oslo S til 2.5 min.; for ankomst til Lillestrøm er den satt til 3 min. og for to like tog etter hverandre er den satt til 3.5 min. Sistnevnte verdi er også benyttet for tilfellet med gruppe 4 foran gruppe 3 fordi disse to gruppene fungerer som like tog over det meste av strekningen (gruppe 3 har sløyfet de to første stoppene sammenliknet med gruppe 4).
| Etterfølgende tog/ Forankjørende tog |
Toggruppe 1 | Toggruppe 2 | Toggruppe 3 | Toggruppe 4 |
|---|---|---|---|---|
| Toggruppe 1 | n = 1 t = 3.5 |
n = 1 t = 2.5 | ||
| Toggruppe 2 | n = 1 t = 3 + 1 |
n = 2 t = 3.5 |
n = 1 t = 2.5 | |
| Toggruppe 3 | n = 2 t = 3 + 4 |
n = 1 t = 3.5 |
||
| Toggruppe 4 | n = 2 t = 3.5 + 2 |
De tomme rutene indikerer kombinasjoner av togfølger som ikke forekommer i listen foran.
På grunnlag av denne tabellen kan vi regne ut den midlere togfølgetid:
[min.]
Den teoretisk maksimalkapasitet i maksimaltimen blir følgelig:
[tog/time]
Denne beregningen gav en vesentlig høyere kapasitet enn i eksempelet med maksimalt blandet trafikk (i kap. 2.2.2). Dette skyldes særlig to forhold:
- Vi har i denne situasjonen en markert puljekjøring, særlig når vi tar med at gruppe 3 og 4 har ganske lik kjøretid.
- Differansen i kjøretid mellom de ulike tog-gruppene er vesentlig mindre her enn i kap. 2.2.2. Dette skyldes både at de raske togene har fått store tillegg i kjøretiden (det mest ekstreme tilfellet er et fjerntog med samme kjøretid som et lokaltog med 9 stopp) og at halvparten av de stoppende togene har sløyfet 2 stopp og således redusert kjøretiden med 2 min.
Det forhold at vi her har brukt hele fire tog-grupper har liten betydning for resultatet når forskjellen mellom noen av gruppene er så liten som her. Dette kan vi se ved å slå sammen gruppe 1 og 2 til en gruppe med kjøretid 19.5 min. og gruppe 3 og 4 til en gruppe med kjøretid 25 min. Ved å bruke samme framgangsmåte som på foregående side får vi at denne inndelingen gir en midlere togfølgetid på 4.22 min. og en teoretisk maksimalkapasitet på 14.2 tog/time.
Utbygging fra 2 til 4 spor
Vi skal også kort omtale konsekvensene av en utbygging fra 2 til 4 spor.
Kapasitets-økningen ved en slik utbygging er sterkt avhengig av rutemønsteret:
- Hvis det i utgangspunktet er ensartet trafikk på dobbeltsporet, blir selvsagt kapasiteten pr. spor uendret ved utbygging til 4 spor, og den totale kapasiteten blir doblet.
- Ved blandet trafikk av i hovedsak to tog-grupper, vil man få ensartet eller tilnærmet ensartet trafikk på hvert spor etter utbygging. Som vi har sett i det foregående, blir det en stor kapasitets-økning pr. spor ved overgang fra blandet til ensartet trafikk. Ved maksimalt blandet trafikk (raske og langsomme tog annen hver gang) blir kapasiteten pr. spor mer enn doblet ved en utbygging fra 2 til 4 spor, og den totale kapasitet blir da mer enn 4-doblet!
Praktisk kapasitet
Den teoretiske kapasitet, som vi har behandlet i det foregående, er tilstrekkelig for f.eks. å sammenlikne ulike utbyggingsalternativer m.h.p kapasitet.
Men når man vil vite hvor mange tog det er forsvarlig å belaste en strekning med i praktisk drift, må vi anslå den praktiske kapasitet. Som nevnt i kap. 1.2, må det da trekkes inn skjønnsmessige forhold, oftest i form av erfaringstall (“tommelfingerregler”).
Den praktisk kapasitet (Kp) kan uttrykkes som en viss andel (u) av den teoretiske kapasitet (Kt):
Denne andelen eller utnyttelsesgraden (u) angir hvor mye av den teoretiske kapasitet som det anses forsvarlig å utnytte.
En annen uttrykksmåte for dette (hentet fra ref. / 1 /) er å gi den midlere togfølgetiden et tillegg (tb) uttrykt som en fraksjon (f) av midlere togfølgetid (tb = ftm). Dette tillegget kalles buffertid og gir uttrykk for at tidsavstanden mellom togene i praksis må være noe større enn den minste togfølgetiden som teknisk er mulig. Den praktisk kapasiteten blir da
Sammenhengen mellom utnyttelsesgraden u og faktoren f i buffertiden kan finnes ved å sette de to uttrykkene for praktisk kapasitet lik hverandre og sette inn for den teoretiske kapasitet. Vi får da likningen
Herav får vi
og videre
Faktoren f som gir forholdet mellom buffertiden og midlere togfølgetid kan altså uttrykkes ved utnyttelsesgraden u som
Følgende erfaringstall for utnyttelsesgraden er gjengitt i ref. / 1 / og stammer visstnok fra DB (Deutche Bundesbahn):
- døgnkapasitet: 60% (3/5) utnyttelse av teoretisk kapasitet
- timekapasitet: 75% (3/4) utnyttelse av teoretisk kapasitet
Ved kortere intervall for max belastning kan enda høyere utnyttelse benyttes. Ved T-banen i Oslo setter man vanligvis 80% utnyttelse i max-kvarteret som den maksimale praktiske kapasitet.
Hvilken utnyttelsesgrad man bør legge seg på (de ovenfor eller andre), avhenger først og fremst av hvor god punktlighet man tilstreber, men også av påliteligheten til alt det tekniske utstyret, dvs. hvor ofte det oppstår primære forsinkelser. Videre spiller det inn hvor dyktige operatørene (toglederne) er i å hindre at (primær-)forsinkelser sprer seg til andre tog.
Eksempel: Vi skal anslå den praktiske kapasitet på strekningen Oslo - Lillestrøm i ettermiddags-rushet. I kap. 2.2.4 ble den teoretiske kapasitet beregnet til 13.75 tog/time. Med den maksimale utnyttelsesgrad for timekapasitet på 75%, som anbefalt i ref. / 1 /, får vi da at den praktiske kapasitet blir 10.3 tog/time. Siden det ble kjørt 11 tog i maksimaltimen, ligger man altså litt over den praktiske kapasitet etter anbefalingen i ref. / 1 /. Den aktuelle trafikk tilsvarer en kapasitetsutnyttelse på 80%.
På JBVs forstadsstrekninger har man i rushtidene noe omkring 75% utnyttelse av teoretisk kapasitet (eksempelet ovenfor representerer antagelig en av de sterkeste kapasitetsutnyttelsene). Kjøretidene for de direkte togene er da økt for å redusere kjøretidsdifferansen og øke kapasiteten, som omtalt på slutten av kap. 2.2.2. En utnyttelsesgrad på ca. 75% gir altså ingen særlig god punktlighet med de ressurser (både teknisk utstyr og personell) som NSB disponerer.
I situasjoner hvor man ønsker vesentlig bedre punktlighet enn det JBV har i dag (tilbringertjeneste til hovedflyplass er et aktuelt eksempel), bør man legge seg på en lavere utnyttelse enn det som er anført ovenfor.
Lengre strekninger
På lengre strekninger er det ofte avgreninger, større stasjoner hvor tog starter eller ender, forbikjøringsmuligheter (for rutemessig bruk) o.l. For å finne kapasiteten for slike lengre strekninger deles strekningen inn i strekningsavsnitt hvor hvert strekningsavsnitt oppfyller de betingelser nevnt innledningsvis i kapitlet. Deretter beregner man kapasiteten for hvert strekningsavsnitt for seg.
Den teoretisk kapasitet for hele strekningen vil da være lik kapasiteten til det strekningsavsnitt med lavest kapasitet, det dimensjonerende strekningsavsnitt.
For den praktisk kapasitet kan det være nødvendig å trekke inn totalstrekningens lengde. Det synes jo rimelig at det er vanskeligere å framføre tog med en viss punktlighet over en lang strekning enn over en kort. Dette er særlig aktuelt hvis kapasiteten er omtrent like stor på de ulike strekningsavsnittene.
Hvis strekningsavsnittet med lavest kapasitet har markert lavere kapasitet enn de øvrige (“flaskehals”), synes det derimot rimelig å la den praktisk kapasitet for strekningsavsnittet også bli den praktiske kapasitet på totalstrekningen.
Med de dobbeltsporstrekninger som JBV i dag har, er de vurderingene som er gjort her lite aktuelle, men i forbindelse med de store utbygginger som nå planlegges, vil man få lengre dobbeltsporstrekninger, og da vil slike vurderinger kunne komme inn.
Under behandlingen av enkeltspor vil vi omtale betydningen av antall strekningsavsnitt og dimensjonerende strekningsavsnitt noe mer da disse begrepene spiller en større rolle ved enkeltspor slik som forholdene er i Norge.
På mange hovedstrekninger på kontinentet er det blandet trafikk av hurtige persontog (IC) og godstog. Det er da vanlig med regelmessige forbikjøringsspor (3. spor) plassert med jevne mellomrom omtrent som kryssingsspor på enkeltsporede strekninger.Ved kapasitetsberegning for slike strekninger må man finne dimensjonerende delstrekning og ta hensyn til antall strekningsavsnitt på tilsvarende måte som beskrevet for enkeltspor (kap. 4.2).
Signalsystem og togfølgetid dobbeltspor
I dette kapitlet skal vi gå nærmere inn på beregning av togfølgetider. Det blir derfor nødvendig å beskrive ulike typer signalsystem da disse har stor betydning for togfølgetidene og dermed for kapasiteten. En del av de kapasitetsmessige betraktninger fra forrige kapittel er det naturlig å videreføre i dette kapitlet.
Elementene som inngår i minste togfølgetid
Den minste togfølgetiden for en strekning er den minste tidsavstanden mellom to tog slik at det andre toget på betryggende måte kan holde sin maksimale hastighet (samme hastighet som det første toget).
Hvis tog 2 skal beholde sin konstante hastighet og dermed konstant (minimum) togfølgetid etter tog 1, må alle signaler vise grønt før toget når fram til dem. Hvis ikke dette er tilfelle, vil tog 2 begynne å bremse, og tidsavstanden mellom togene vil øke.
Det basale sikkerhetskravet er at det alltid skal være minst en bremselengde fritt spor foran toget. Avhengig av det signalsystemet som benyttes, vil det i praksis bli et større eller mindre tillegg til dette basis-kravet. Figur 4 m.fl. viser de elementene som inngår i den minste togfølgetiden.
I det følgende omtales de enkelte elementene i togfølgetiden.
Siktavstand
Selv om det alltid er tilstrekkelig bremselengde fra det første restriktive signal til stopp-punktet, vil en lokomotivfører normalt begynne å redusere hastigheten et stykke før signalet istedenfor nøyaktig der signalet står. Dette kan dels skyldes forsiktighet, dels det forhold at bremsing øker sannsynligheten for at signalet skifter til grønt før toget passerer det slik at full hastighet kan gjenopptas. Det punktet hvor bremsing innledes kalles iblant - særlig i engelsk litteratur - for siktpunktet, og avstanden til signalet for siktavstanden (“sighting point / distance”). I denne betydning av ordet er siktavstanden ofte kortere enn avstanden fra det punkt hvor føreren først ser signalet. I andre sammenhenger, f.eks. vurdering av signalplassering ute i terrenget, brukes ordet siktavstand i den sistnevnte og mer naturlige betydningen. I dette notatet vil vi bruke ordet i den førstnevnte betydningen. Det samme gjelder også når man gir inn data til en del simuleringsmodeller som regner så nøyaktig at de tar hensyn til dette forholdet.
Siktavstanden i førstnevnte betydning vil variere fra fører til fører og fra strekning til strekning. Den kan angis som en lengde eller relateres til tid, altså hvor lenge før signalet føreren vil begynne å bremse. Bruk av tidsavstand synes oftest som det mest rimelige, spesielt i slike teoretisk betraktninger som her.
For tallberegninger kan 10 sekunder anses som en rimelig verdi.
Et moment som ikke er vist på figurene, er den tekniske reaksjonstiden, dvs. tiden fra et tog frigir en blokkstrekning til dette vises på signalene bak toget. For automatiske systemer er denne tiden normalt så liten at den kan neglisjeres i beregningene. I spesielle situasjoner hvor det inngår manuelle ledd i “signaleringskjeden”, er det viktig å få dette med i beregningen av togfølgetiden.
Blokkstrekninger og bremselengde
Denne delen av togfølgetiden består av avstanden fra det første restriktive signalet til stopp-punktet (rødt signal). Den består av et antall blokkstrekninger; antallet avhenger av signalsystemet. Den kan ikke under noen omstendighet være kortere enn bremselengden for det toget som har lengst bremselengde av de togene som tillates å trafikkere strekningen (det dimensjonerende toget). I situasjoner hvor det ikke er behov for å utnytte strekningen maksimalt kan denne avstanden være vesentlig lengre, noe som gir et rimeligere signalanlegg.
Sammenhengen mellom blokklengde og bremselengde varierer med type signalsystem og omtales under de enkelte signalsystemene.
Ved JBV er det på de fleste eksisterende strekninger brukt en “standard” bremselengde på ca. 800m. Dette har sammenheng med at både persontog med toppfart 120-130km/h og godstog med toppfart 80-90km/h har omtrent denne bremselengde. Ved andre forvaltninger er det vanlig at man har bremsekurver/tabeller med bremselengde som funksjon av hastighet og stigning/fall. Ved planlegging av nyanlegg og oppgradering av eksisterende anlegg regner man også i JBV med betydelig høyere hastigheter og lengre bremselengder.
Denne avstanden (fra det første restriktive signalet til stopp-punktet) utgjør nesten alltid hoveddelen av togfølgetiden, og det er denne avstanden man kan påvirke gjennom valg av signalsystem og signalplassering.
Ved design av et signalanlegg må man velge dimensjonerende hastighet og dermed bremselengde. Strekningen kan da normalt ikke trafikkeres av tog med høyere toppfart med mindre disse tog har så gode bremser at de kan stoppe fra sin toppfart innen det dimensjonerende togets bremselengde.
Toglengde
Toglengden er den siste faktoren som inngår i togfølgetiden. For persontrafikk, hvor togene normalt er forholdsvis korte, har den ganske liten innflytelse på resultatet rent tallmessig. Et klart unntak er situasjoner med ekstremt korte blokklengder slik som f.eks. i beregningen av den optimale kapasitet i kap. 2.1.
For godstog som normalt er vesentlig lengre og har lavere hastighet, vil toglengden gi et vesentlig bidrag til togfølgetiden. Derfor er vanligvis togfølgetiden mellom to godstog vesentlig større enn mellom to persontog.
Omtale av ulike signalsystem
Det aller enkleste form for signalsystem (med lys) består av bare en type signaler som kan vise to signalbilder:
- rødt (stopp) når det er et tog på strekningen fram til følgende signal
- grønt (kjør) når tilsvarende strekning er ledig.
Dette er et system med 2 begrep (= signalbilder), og det kan kun brukes for systemer hvor hastigheten er så lav at det er tilstrekkelig å bremse når man ser det røde signalet (f.eks. trikkelinjer). Hvert signal er logisk (og elektrisk) knyttet til den etterfølgende strekning fram til neste signal. En slik strekning kalles ofte blokkstrekning (et eller flere elektrisk isolerte sporfelt), og når det er et tog på denne strekningen viser signalet alltid rødt.
Tog har generelt lange bremsestrekninger pga. den lille friksjonen det er mellom stålhjul og stålskinne. Det skal derfor ikke særlig høy hastighet til før bremselengden blir så lang at det er nødvendig å begynne å bremse før føreren ser det røde signalet. Det må da settes opp et signal på det stedet hvor bremsing må starte, som gir et forvarsel om at neste signal viser stopp. Et slikt signal kalles et forsignal, mens de opprinnelige kalles hovedsignaler. Et forsignal er logisk knyttet til etterfølgende hovedsignal og ikke til noe eget sporfelt.
JBVs ordinære signalsystem består av slike forsignaler og hovedsignaler. Hovedsignalet har 3 lys med følgende signalbilder og betydninger:
- rødt: stopp (tog på neste blokkstrekning)
- et grønt: kjør med lav hastighet (fordi det er en sporveksel i avvik på neste blokkstrekning)
- to grønne: kjør med full hastighet (ingen sporveksel i avvik på neste blokkstrekning)
Forsignalet har to lys med følgende signalbilder og betydninger:
- blinkende gult: tilhørende hovedsignal viser rødt
- blinkende gult og grønt: tilhørende hovedsignal viser ett grønt
- blinkende grønt: tilhørende hovedsignal viser to grønne
JBVs signalsystem med separate for- og hovedsignaler er typisk egnet for enkeltspor. På dobbeltsporstrekninger med tett trafikk trenger man korte blokklengder (dvs. ikke vesentlig lengre enn dimensjonerende togs bremsestrekning), og da må forsignalet settes på foregående hovedsignals mast. Man får da et såkalt 3-begrep signalsystem, men med 5 lys fordi informasjon om eventuell avvikende sporveksel fortsatt er med. I et rent 3-begrep signalsystem brukes vanligvis bare 3 lys med følgende betydninger (vanlig fargebruk er også angitt):
- rødt: stopp (tog på neste blokkstrekning)
- gult: vent stopp (neste signal viser nå stopp, dvs. det er en bremselengde til stopp-punktet, og bremsing må umiddelbart iverksettes)
- grønt: kjør (neste signal viser minst gult, dvs. det er minst to bremselengder til forangående tog, og full hastighet kan holdes fram til neste signal)
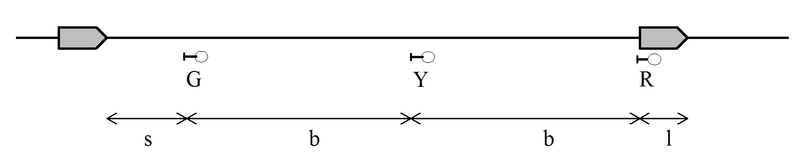
De kapasitetsmessige forhold avhenger ikke av hvordan man signalerer de ulike begrepene. I det følgende vil de sistnevnte betegnelsene brukes, og når det trengs forkortelser (figurer o.l.) brukes for enkelhets skyld de engelske forkortelsene R, Y og G.
Ved 3-begrep signalering er det alltid minst en bremselengde (for dimensjonerende tog) mellom signalene og følgelig minst to bremselengder mellom togene. Hvis det trengs høyere kapasitet, må avstanden mellom togene reduseres. Dette kan gjøres ved å innføre et 4. begrep, dvs. forsignalering over to blokkstrekninger. Da begynner toget å bremse to blokklengder før stopp-punktet, og dermed kan blokklengden reduseres til halvparten av dimensjonerende togs bremselengde.
For 4-begrep systemer varierer signalbildene mer fra land til land. I det følgende beskrives de engelske signalbilder. Det brukes der 4 lys med følgende signalbilder (vanlig forkortelse er også angitt):
- rødt (R): stopp (tog på neste blokkstrekning)
- et gult (Y): vent stopp (neste signal viser nå stopp, dvs. det er mindre enn en bremselengde til stopp-punktet; fortsett bremsing)
- to gule(YY): innled bremsing (det er en bremselengde til stopp-punktet)
- grønt (G): kjør (neste signal viser minst to gule, dvs. full hastighet kan holdes fram til neste signal)
4-begrep signalsystem er til nå ikke tatt i bruk ved JBV. Det foreligger imidlertid et forslag om anvendelse av nåværende signalbilder til 4-begrep signalering. Dette forslaget innebærer at ett grønt lys i hovedsignalet også kan bety at det er mindre enn en bremselengde til stopp-punktet, altså at hastigheten må være lavere enn maksimalhastigheten.
Togfølgetidene kan ytterligere reduseres og kapasiteten økes ved å innføre enda flere begrep. Generelt kan man snakke om n-begrep signalering. Med økende antall begrep blir det mer upraktisk med bare utvendige signaler, og det brukes da oftest innvendig signalering (førerrom-signalering, “cab signalling”) som angir hastighet direkte istedenfor signalbilder.
Systemer som gir lokomotivføreren kontinuerlig informasjon om avstanden til forangående tog, omtales som systemer med rullende eller dynamisk blokk (i motsetning til den ordinære statiske blokkdelingen). Ved bruk av slike systemer kan det tillates at avstanden mellom to tog bringes ned mot en dimensjonerende bremselengde. Rent matematisk kan dette betraktes som et system med svært mange begrep (n tilnærmet uendelig).
Hvis systemet er slik at denne bremselengden ikke er relatert til det dimensjonerende toget for strekningen slik som ved en statisk blokkdeling, men beregnes kontinuerlig ut fra hastigheten for det aktuelle toget, betegnes systemet som kjøring på elektronisk sikt. Avstanden mellom togene kan altså da være kortere enn bremselengden for det dårligst bremsende tog som tillates på strekningen. Videre er denne bremselengden og dermed den minimale avstanden til forangående tog også avhengig av den aktuelle hastigheten slik at avstanden til forangående tog kan reduseres når togets hastighet reduseres.
For disse systemer er det selvsagt kun aktuelt med innvendig signalering (selv om det ofte også fins et vanlig ytre system som tjener som reserve, samt som signalering for tog uten det kontinuerlige systemet). Vi vil her ikke gå nærmere inn på virkemåten for slike systemer. I det følgende vil kontinuerlige systemer (eller uendelig mange blokkstrekninger) bli brukt som grensetilfelle for den minste togfølgetid som kan oppnås.
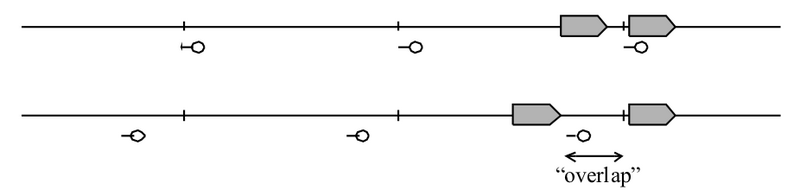
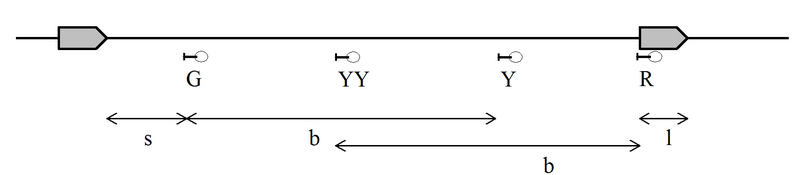
Tradisjonelle ytre signaler er alltid relatert til en blokkstrekning (ett eller flere isolerte sporfelt). Men det er noe ulik praksis når det gjelder plassering av signalet i forhold til det fysiske delepunkt mellom blokkstrekningene (“isolert skjøt”). Ved JBV skal signalet plasseres ved dette delepunktet. Ved en del andre jernbaner, bl.a. BR (British Railways), plasseres signalet alltid et stykke før den (logisk) tilhørende blokkgrense, se figur nedenfor.
Figur 3: Signalplassering i forhold til blokkgrense, ved JBV (øverst) og BR (nederst). Figuren viser også teoretisk minste togseparasjon (ved stillstand).
Avstanden fra signalet til blokkgrensen kalles i britisk litteratur for “overlap”. Denne utgjør en sikkerhetssone fra signalet til togvegens slutt, og er den minste separasjonen som kan oppnås mellom to tog (dvs. ved stillstand). Ved BR har denne sonen en lengde på 2-300 yards. Den inngår alltid i togfølgeberegninger. Bruk av en slik sone medfører at blokklengdene strikt kan fastlegges etter dimensjonerende togs bremselengde uten noe sikkerhetsmessig “påslag”. På alle figurer som i det følgende er hentet fra britisk litteratur, vil man finne denne sonen.
Beregning av togfølgetider ved konstant hastighet og blokklengde
Når en strekning har konstant hastighet og like lange blokklengder, er det enkelt å beregne togfølgetidene.
Denne type beregninger er hovedsaklig egnet til å anslå kapasitet før en endelig signalplassering er fastlagt eller som grove overslag uten å gå inn på detaljer i signalplasseringen. Videre er de egnet til generelt å demonstrere den kapasitetsmessige virkning av slike ting som å innføre stopp, endre signalsystemet fra 3- til 4-begrep o.l.
Strekning uten stopp
I denne situasjonen forutsetter vi at det ikke foregår noen akselerasjon eller retardasjon noe sted på strekningen. Med 3-begrep signalering blir situasjonen ved minste togfølgetid da som på figuren nedenfor.
Figur 4: Minste togfølgetid ved 3-begrep signalering.
Her betegner b blokklengden som i dette tilfellet er identisk med en standard bremselengde. Togenes lengde kalles L, og togfølgetiden uttrykkes da ofte som
hvor s er siktavstanden, og det forutsettes da at lokføreren begynner å bremse denne avstanden før et restriktivt signal. Det virker kanskje mer rimelig at denne avstanden er proporsjonal med hastigheten, og togfølgetiden kan da uttrykkes
hvor ts er “siktavstanden”, dvs. tiden som går med til å kjøre siktavstanden (ts = s/v).
Ved 4-begrep signalering blir situasjonen som vist nedenfor:
Figur 5: Minste togfølgetid ved 4-begrep signalering.
b betegner fortsatt en standard bremselengde, men denne tilsvarer nå 2 blokkstrekninger. Med for øvrig de samme betegnelsene som ovenfor blir minste togfølgetid
Generelt har vi for et n-begrep system (forsignalering over n-1 blokkstrekninger) at togfølgetiden blir
Når n er meget stor, blir togfølgetiden tilnærmet
Man snakker da om kontinuerlige systemer eller dynamisk (rullende) blokk.
Strekning med stopp
Vi ser nå på en strekning hvor det fortsatt er (tilnærmet) like tog med konstant hastighet v og bremselengde (blokklengde) b, men hvor alle tog har et stopp. Det er altså fortsatt snakk om ensartet trafikk. Videre forutsetter vi her konstant akselerasjon (a) og retardasjon (r).
Innføring av et stopp (i hovedsporet, altså uten noen ekstra spor) fører til at togfølgetiden øker vesentlig fordi blokkstrekningen som inneholder stoppestedet, blir belagt i vesentlig lengre tid. Dette er illustrert i Figur 10.
Togfølgetiden med stopp kan uttrykkes som togfølgetiden uten stopp samt et tillegg. Dette tillegget består av det økte tidsforbruket pga. akselerasjon og retardasjon, samt oppholdstiden ved plattform (to).
Tidstillegget pga. en retardasjon og akselerasjon er
Togfølgetiden for en strekning med stopp blir da ved 3-begrep signalering
Ved 4-begrep signalering blir den tilsvarende
Ved flere begrep generaliseres uttrykket på samme måte som uten stopp.
Vanligvis er retardasjonen for et tog noe høyere enn akselerasjonen fordi et tog normalt bremser på alle aksler, men ikke har trekk-kraft på alle. For overslagsberegninger slik som her, og for nåværende norske hastighetsforhold er det likevel en god tilnærmelse å sette akselerasjonen lik retardasjonen. Det vil vi gjøre i de fleste tallberegninger i det følgende.
Vi skal nå se på optimalisering av kapasiteten på samme måte som i kap. 2.1, dvs. vi skal finne den hastighet som gir maksimal kapasitet når det er et stoppested på strekningen hvor alle tog stopper. Som forrige gang, gjør vi dette for 3-begrep signalering og setter bremselengden (og blokklengden) til
For enkelhets skyld setter vi a = r, og uttrykket for den teoretiske kapasiteten blir da
Ved derivasjon m.h.p. v og noe regning kommer vi fram til at den optimale hastigheten nå er gitt ved
Eksempel: Vi skal anslå den optimale hastigheten for en strekning med ensartet trafikk av typiske nærtrafikktog som alle har stopp. Vi bruker de samme verdiene som i eksempelet i kap. 2.1 (L = 200 m, r = 1 m/s2, s = 100 m). Dette gir
Den optimal hastighet blir følgelig 11.5 m/s (42 km/h) mot nesten det dobbelte i tilfellet uten stopp. En så lav hastighet er selvfølgelig helt uinteressant i praksis.
Den tilhørende maksimale kapasitet per tidsenhet blir (med 10 sekunders siktavstand, 40 sekunders oppholdstid og a = r)
[tog/time]
Dette er mer enn en halvering sammenliknet med tilsvarende situasjon uten stopp (K = 72 tog/time). Hvis vi bruker den optimale hastigheten (og bremselengden) for situasjonen uten stopp som ble funnet i kap. 2.1, synker den teoretiske kapasiteten ytterligere, til ca. 27 tog/time. At reduksjonen ikke er større, skyldes at blokklengdene her er så (urealistisk) korte at det konstante tillegget (s) som vi satte til 100 m utgjør en stor del av blokklengden.
Vi har altså sett at det å innføre et stopp (for alle tog) på en strekning hvor det før ikke var stopp, fører til en drastisk reduksjon av kapasiteten. Et stopp i hovedsporet på en dobbeltsporstrekning kan altså betraktes som en (lokal) flaskehals fordi togene oppholder seg så mye lengre der enn andre steder på strekningen. Skal kapasiteten opprettholdes på omtrent samme nivå ved innføring av stopp, må stoppestedet/stasjonen ha flere spor, altså økt kapasitet i flaskehalsen.
Uttrykkene for togfølgetid og kapasitet blir de samme hvis det er flere stopp for alle tog på strekningen. Stoppestedet med lengst oppholdstid er da bestemmende for kapasiteten.
Grafisk beregning av togfølgetider
I det foregående har vi forutsatt at både hastighet og blokklengde er konstante over en lengre strekning. I mange andre land er det ofte konstant maksimalhastighet over lange strekninger, og siktforholdene er gode slik at signalene kan plasseres med jevne intervaller. I Norge er hastighetsstandarden - i tillegg til å være lav - også meget varierende. Det er sjelden mer enn noen få km i trekk med samme hastighet. Pga. terrenget er det ofte vanskelig å plassere signaler slik at det blir tilstrekkelig sikt, og blokklengden (signalavstanden) vil derfor i praksis variere fra signal til signal. Beregningene i foregående avsnitt kan derfor bare benyttes til overslag. Hvis man skal ha mer nøyaktige togfølgetider, må man gå grundigere til verks.
I det følgende vil vi vise noen eksempler på hvordan man kan finne togfølgetider ut fra grafer. Det brukes da detaljerte tid-veg diagrammer, ikke skjematiske (grafiske ruter) som vist tidligere.
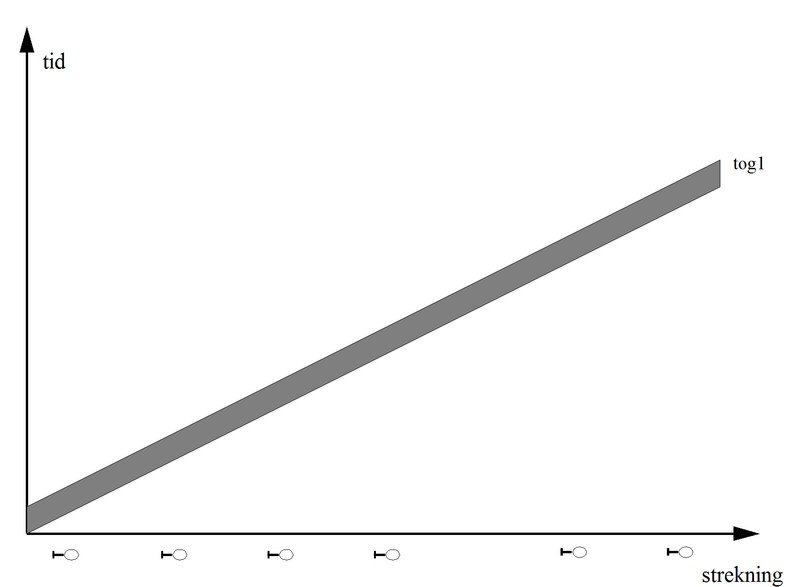
Først vises over fire figurer hvordan man tegner et slikt togfølge-diagram. I disse figurene er det konstant hastighet uten stopp, men signalavstandene er ujevne. Man begynner med å tegne aksene, og signalplasseringen markeres på strekning-aksen. Så tegnes en nøyaktig kurve som viser både fronten og enden av det første toget. Følgende figur viser dette.
Figur 6: Begynnelsen av togfølge-diagram.
Videre tegnes for hvert blokkskille en vertikal linje opp til kryssingspunktet med linjen som markerer enden av det første toget, og deretter føres linjen horisontalt bort til tids-aksen. Disse linjene er stiplet på figuren nedenfor. I denne figuren er det forutsatt at signalet står ved blokkskillet (norske forhold). Disse horisontale linjene markerer når hvert signal skifter mellom de ulike begrepene fra stopp (rødt) til høyeste begrep (grønt). Signalbildene er også påført figuren.
Figur 7: Togfølge-diagram med første tog og signalbilder bak toget.
Man har nå de nødvendige opplysninger for å plassere kurven for fronten av det andre toget slik at man oppnår minimal togfølgetid. Det kan kreve noe prøving og feiling å finne den plassering av kurven som gir minimal togfølgetid hvis det ikke er opplagt hvor det kritiske punktet (signalet) er. I figuren ovenfor er det selvsagt den lengste blokkstrekningen som er dimensjonerende, og vi ser at dette gir seg utslag ved at det tar vesentlig lengre tid å få grønt i de to signalene rett før denne blokkstrekningen enn i de øvrige signalene.
I neste figur er kurven for fronten av det andre toget plassert. Siktavstand må medtas når man plasserer denne kurven.
Figur 8: Fullstendig togfølge-diagram inklusive hjelpelinjer.
Man kan nå direkte lese av togfølgetiden på tidsaksen.
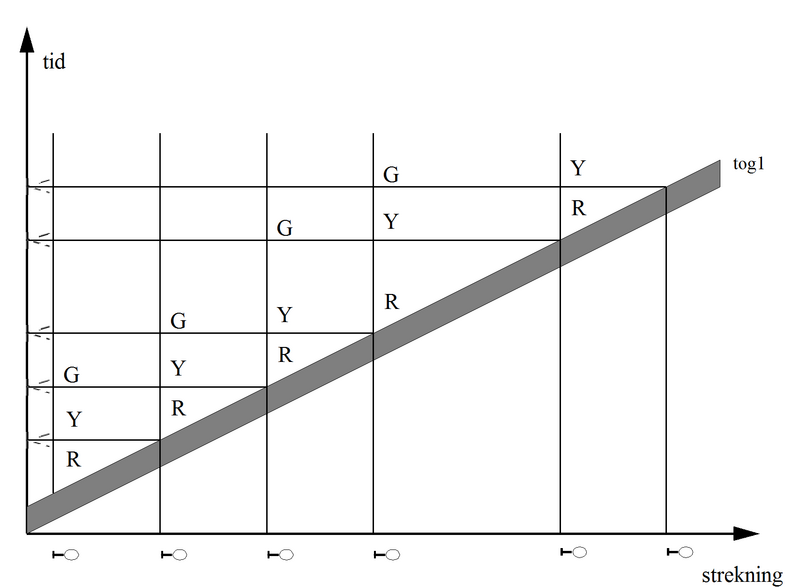
I den neste figuren er hjelpelinjene fjernet for å vise hvordan togfølge-diagrammene ofte framstår.
Figur 9: Fullstendig togfølgediagram slik de oftest vises (hjelpelinjer fjernet).
I denne enkle situasjonen vil det, som tidligere nevnt, være den lengste blokkstrekningen som er dimensjonerende, og det kritiske punkt (signal) blir et av de to rett før den kritiske blokkstrekningen.
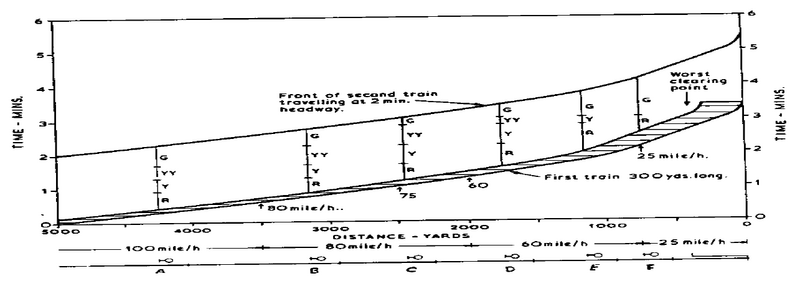
I det følgende skal vi se på noen ferdige togfølgediagrammer (“headway diagrams”) for situasjoner med varierende hastighet, stopp m.m. Figurene er hentet fra ref. / 3 / og gjengir engelske forhold. Det brukes derfor gjennomgående 4-begrep signalering med de vanlige forkortelsene R, Y, YY og G, samt “overlap”.
Togfølge-diagram for viktige situasjoner
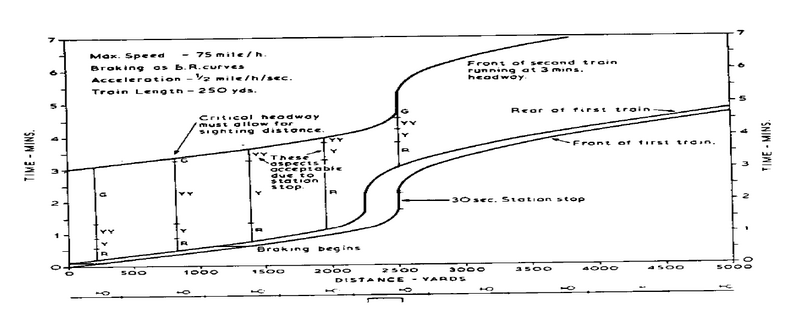
Når man har et stopp i hovedsporet fører dette til vesentlig økt togfølgetid og redusert kapasitet som tidligere omtalt, bl.a. i kap. 3.3.2. Følgende figur viser dette tydelig.
Figur 10: Togfølge-diagram for strekning med konstant hastighet med stopp.
Som man ser helt til venstre i figuren, kunne togfølgetiden i dette tilfellet ha vært ca. 1.5 min. hvis togene ikke hadde hatt stopp, mens den med stopp (den viste linje) er 3 min.
En vesentlig årsak til økningen i togfølgetid er at det vanligvis forutsettes at passerende tog skal kunne holde full hastighet slik at signalavstanden må være den samme som på strekningen for øvrig. Hvis det er en driftsmessig forutsetning at alle tog skal stoppe (kan være aktuelt for T-baner), kan signalavstanden reduseres, og togfølgetiden blir noe mindre. Dette vises det eksempler på senere i dette kapitlet under omtale av kjøring ut fra eller inn til stasjon.
I neste figur vises effekten av en kraftig hastighetsreduksjon på en strekning med konstant signalavstand.
Figur 11: Togfølge-diagram for hastighetsreduksjon og konstant signalavstand.
Vi ser at virkningen blir omtrent som for et stopp (figuren viser et ekstremt eksempel med en hastighetsreduksjon til femteparten av maksimalhastigheten).
De kritiske punktene, som hindrer redusert togfølgetid, er her ved signal A og D. Vi skal se litt nærmere på muligheten for å redusere togfølgetiden ved endret signalplassering. Både strekningene AC og BD må være minst en dimensjonerende bremselengde fordi toget kan ha maksimal hastighet ved siktavstand på de tilhørende signalene. Blokkstrekningen DE kan derimot reduseres, men dette påvirker ikke signaleringen ved A som er kritisk for togfølgetiden. Dermed kan togfølgetiden ikke reduseres fordi eneste mulighet for å få grønt tidligere i signal A ville vært en reduksjon av lengden AD.
Vi ser altså at togfølgetiden blir lengre ved varierende hastighet enn ved konstant hastighet.
Vi ser så på situasjonen hvor to tog kjører ut fra en større stasjon, dvs. enten en sekkestasjon (buttspor) eller en stasjon hvor det er en forutsetning at alle tog stopper eller hvor tillatt hastighet over stasjonen er vesentlig lavere enn linjehastigheten.
Det kan brukes kortere signalavstander ut fra en slik stasjon fordi hastigheten her nødvendigvis må være lavere enn ute på linjen.
Figur 12: Togfølgediagram for to tog som starter fra en stasjon.
Det er her benyttet 3-begrep signalering på de to første signalene fordi hastigheten her er så lav. Dette er vanlig praksis ved 4-begrep signalering og medfører at det andre toget får grønt tidligere enn det ville ha gjort ved bruk av 4 begrep på alle signaler.
Av figuren ser man at det her er forutsatt at togets front står helt i enden av plattformen og altså rett ved det første signalet.
På denne figuren går det ca. 20 sekunder fra det andre toget får grønt i første signal til det starter. Det må tas hensyn til en vesentlig lengre reaksjonstid for et tog ved plattform enn for et tog som stopper for rødt ute på linjen. Dette skyldes at man oftest ikke lukker dører og gjør klar til avgang før man har fått grønt. (Ved NSB også konduktørens avgangssignal, eventuelt også fra togekspeditør.) Hvis denne prosedyren starter når toget får signal Y, vil togfølgetiden kunne reduseres da man tydelig ser av figuren at det er forholdene ved første signal som er begrensende. Det kan være litt forskjellig praksis ulike steder på dette punkt, så dette er et viktig moment å undersøke ved beregning av togfølgetider ut fra slike stasjoner.
Neste figur viser forholdene inn til en liknende stasjon. Det er her forutsatt trinnvis redusert hastighet inn mot stasjonen og signalavstandene minsker i samsvar med dette.
Figur 13: Togfølgediagram for to tog som ankommer en større stasjonen.
Det innerste signalet skifter direkte fra rødt til grønt fordi togene går til hvert sitt spor.
Vi ser at det kritiske punktet er når det andre toget nærmer seg signalet merket C fordi det her er grønt kortest tid. Dette signalet skifter til grønt i det blokkstrekningen EF frigis, og det er altså avstanden fra signal C til F som begrenser togfølgetiden i denne situasjonen.
Kapasitetsøkning ved innføring av flere begrep i signalsystemet
Vi skal her se på den teoretiske kapasitetsøkning ved overgang fra et 3-begrep signalsystem til et 4-begrep system og til “grenseverdien” dynamisk blokk (uendelig mange begrep). Det forutsettes for det meste konstant blokklengde, hastighet, akselerasjon og retardasjon slik at uttrykkene som er utledet i kap. 3.3 kan brukes. For mer nøyaktig beregning av kapasitetsøkningen på en konkret strekning må togfølgetidene finnes mer nøyaktig, f.eks. slik som beskrevet i kap. 3.4.
Strekning uten stopp
Vi ser først på ensartet trafikk uten stopp. Med togfølgetidene fra kap. 3.3.1 ser vi at den teoretiske kapasiteten for et 3-begrep system blir
For et 4-begrep system får vi tilsvarende
Vi ser at kapasiteten øker, men hvor mye den øker avhenger av størrelsen på l + vts i forhold til bremselengden b. Vanligvis er b den dominerende, spesielt ved høye hastigheter.
Den maksimale virkning av overgang fra 3 til 4 begrep får vi når l + vts er neglisjerbar i forhold til b. Togfølgetiden kan altså maksimalt reduseres med 25% ([2 - 1.5] / 2), og kapasiteten øker maksimalt med 33% (2 / 1.5 = 1.33).
Den maksimale reduksjon av togfølgetiden som det er mulig å oppnå, får man ved et kontinuerlig system hvor togene kan kjøre med ned mot en bremselengdes avstand. Ved korte tog vil togfølgetiden kunne bli redusert til bortimot halvparten med et slikt system sammenliknet med et 3-begrep system. Tilsvarende vil kapasiteten kunne øke til bortimot det dobbelte.
Strekning med stopp
Vi ser så på ensartet trafikk med stopp for alle tog. Vi bruker også her tilnærmelsen a= r.
Med togfølgetidene fra kap. 3.3.2 ser vi at den teoretiske kapasiteten for et 3-begrep system er
For et 4-begrep system får vi tilsvarende
Vi ser at kapasiteten øker, men hvor mye den øker avhenger av størrelsen på bremselengden b i forhold til de andre faktorene.
For å få et inntrykk av den maksimale kapasitetsøkning som kan oppnås ved overgang fra 3 til 4 begrep lar vi som ovenfor L + vts være neglisjerbar i forhold til b, og vi lar også oppholdstiden (to) være neglisjerbar selv om dette er en atskillig grovere tilnærmelse. Forholdet (kvotienten) mellom kapasiteten ved h.h.v 4 og 3 begrep blir da
Hvis vi videre gjør den vanlige antagelsen , får vi
Vi får altså at kapasitetsøkningen ved overgang fra 3 til 4 begrep maksimalt blir 10% selv om alle tilnærmelsene vi har gjort har bidratt til å øke dette tallet.
Det eneste tilfellet hvor man kunne tenke seg en høyere kapasitetsøkning i denne situasjonen (ensartet trafikk med stopp), er at blokklengden av en eller annen grunn må holdes vesentlig større enn v2/2r.
Den maksimale reduksjon av togfølgetiden som det er mulig å oppnå, får man ved et kontinuerlig system hvor togene kan kjøre med ned mot en bremselengdes avstand. Den teoretiske kapasiteten i dette tilfellet får man ved å erstatte faktoren 1.5 i K4 med faktoren 1. Denne kapasiteten sett i forhold til kapasiteten ved 3 begrep blir da
Ved samme antagelse som ovenfor (b = v2/2r) ser vi at vi maksimalt kan få
altså maksimalt 20% kapasitetsøkning.
Vi ser altså at ikke bare blir kapasiteten vesentlig lavere på en strekning hvor alle togene har stopp i hovedsporet, men muligheten til å øke kapasiteten ved å innføre mer avansert signalering er også mindre.
Et signalsystem som tillater “kjøring på elektronisk sikt” vil kunne gi noe lavere togfølgetider (og høyere kapasitet) fordi kravet til fri strekning foran det andre toget beregnes kontinuerlig ut fra togets hastighet. Etter som toget bremser, vil således kravet til fri strekning (bremselengden til full stopp) minske, og det andre toget vil kunne komme noe nærmere det første enn med et system hvor togseparasjonen bestemmes av en fast avstand (dimensjonerende bremselengde).
Blandet trafikk
Vi går så over til å se på blandet trafikk, dvs. blanding av tog som har ulike kjøretider over strekningen. Dette skyldes vanligvis ulikt stoppmønster eller ulik topphastighet. På JBVs dobbeltsporstrekninger er det hovedsaklig ulikt stoppmønster som er årsak til differanse i kjøretid, så vi skal derfor konsentrere oss om dette tilfellet. Situasjonen er imidlertid ganske analog når årsaken er ulik topphastighet.
Vi ser først på maksimalt blandet trafikk, dvs. raske og langsomme tog annen hver gang; i praksis vil dette da si stoppende og direkte (eller nesten direkte) tog. Dette er typisk for JBVs dobbeltspor i rushtidene. Et tid-veg diagram for en slik strekning ser da typisk ut som følger:
Figur 14: Mer detaljert grafisk rute med blandet trafikk.
Denne figuren er noe mer detaljert enn de figurene som tidligere er vist for denne situasjonen. Vi har her tatt med at frem til bremsepunktet for første stopp (det punkt der bremsing innledes) har man tilnærmet ensartet trafikk. Dette skyldes at ved NSB har (for tiden) de materielltyper som benyttes i persontog omtrent lik yteevne (toppfart, akselerasjon, retardasjon). I mange andre land vil situasjonen ofte være at de stoppende (lokale) togene har vesentlig lavere topphastighet enn de direkte (f.eks 100 mot 160 eller 200 km/h). Figuren ovenfor er ikke helt representativ for slike situasjoner hvis de direkte togene oppnår en hastighet godt over de stoppende togenes toppfart innen bremsepunktet for første stopp.
For å beregne kapasiteten trenger vi da togfølgetiden for delstrekningen fra utgangsstasjonen til første stoppested (t1) og for delstrekningen fra siste stoppested til endestasjonen (t2). Disse to delstrekningene vil bli omtalt som endepartiene av strekningen. Utgangs- og endestasjonen refererer her til strekningen og ikke til togene. Disse togfølgetidene finnes slik som beskrevet i det foregående. Videre trenger vi differansen i kjøretid mellom de to togtypene over hele strekningen (Δt). Den midlere togfølgetid blir da
Den teoretiske kapasiteten blir
Mellom første og siste stoppested vil tidsavstanden mellom togene være merkbart større enn på endepartiene fordi hvert stopp medfører et tidstap på ca. 1 min. eller mer. En endring av signalsystemet vil derfor påvirke t1 og t2, men ikke Δt. Den kapasitetsmessige virkning av å innføre et mer avansert signalsystem blir derfor vesentlig mindre ved blandet trafikk enn med ensartet trafikk uten stopp (i hovedsporet). Som vi har sett i det foregående vil man maksimalt kunne halvere togfølgetiden ved å gå fra et ordinært 3-begrep system til et kontinuerlig system (dynamisk blokk). Siden t1 og t2 selv med et ordinært 3-begrep system vil kunne få verdier på ca. 2 min., mens Δt vil være vesentlig større (10 min. er en passende verdi for JBVs strekninger), ser vi at kapasiteten ikke øker mer enn i størrelsesorden 10% ved overgang fra det helt enkle signalsystem til det mest avanserte system. Det understrekes at vi her ser på maksimalt blandet trafikk, at togene i hver gruppe er like, trafikkerer hele strekningen osv.
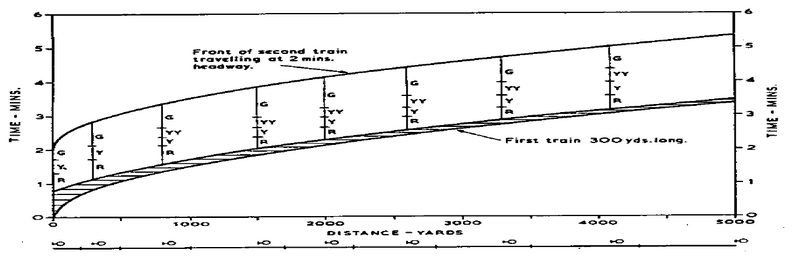
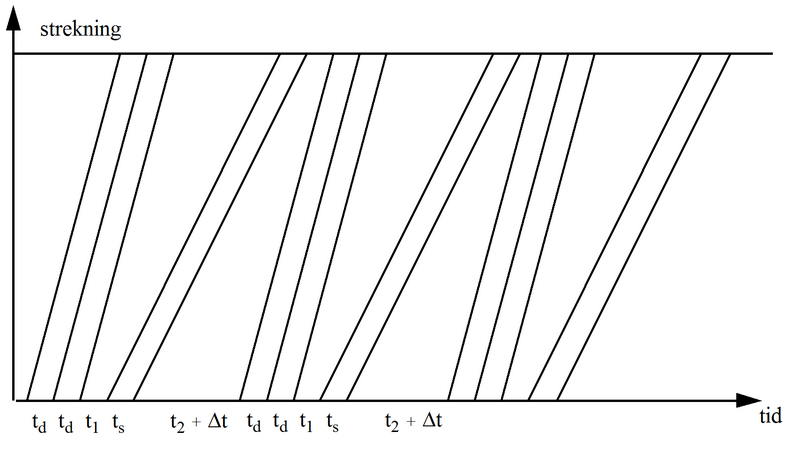
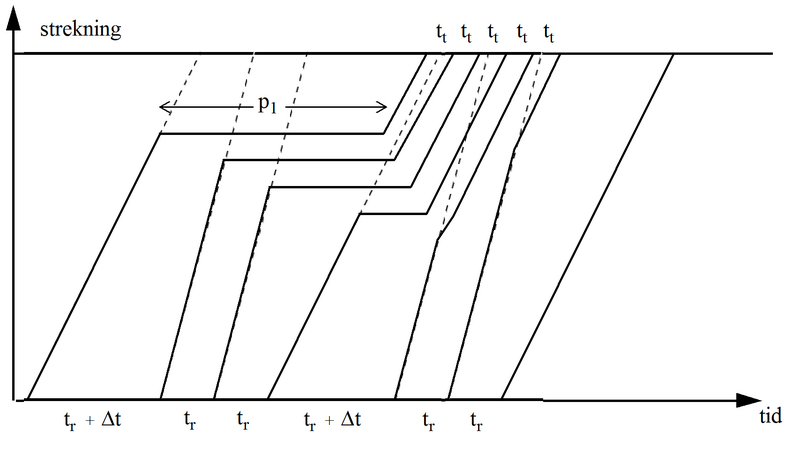
Hvis vi kjører flere like tog etter hverandre, blir kapasiteten høyere som tidligere vist. Vi skal nå se på en situasjon hvor det vekselvis kjøres n direkte tog og m stoppende tog. På følgende figur er vist et eksempel med n = 3 og m = 2. Videre er togfølgetidene påført. (For JBVs nåværende dobbeltsporstrekninger kan det i praksis neppe tenkes andre tilfeller enn m=1.)
Figur 15: Grafisk rute med puljer på 3 direkte og 2 stoppende tog.
Vi har da n-1 tilfeller med direkte tog etter direkte (togfølgetid td), ett tilfelle med stoppende etter direkte (togfølgetid t1), m-1 tilfeller med stoppende etter stoppende (togfølgetid ts) og ett tilfelle med direkte etter stoppende (togfølgetid t2 + Δt). Den midlere togfølgetid for alle n + m togene blir da
og kapasiteten blir
Som vi har sett i det foregående vil overgang fra 3 til 4 begrep redusere td, t1 og t2 betydelig, ts noe, mens Δt fortsatt vil være uendret. Kapasitetsøkningen ved bedret signalsystem blir altså noe større når trafikken er mindre blandet.
Som hovedkonklusjon vil vi da si at kapasitetsøkningen ved innføring av flere begrep i signalsystemet er meget stor ved ensartet trafikk uten stopp (eller med stopp bare der det er flere spor slik at kapasiteten på stoppestedene er like stor som på linjen).
I andre situasjoner er kapasitetsøkningen mer begrenset, men kan likevel i mange tilfelle være et kostnadseffektivt tiltak.
Innføring av 4-begrep signalsystem som ledd i hastighetsøkning
Vi skal også omtale en spesiell situasjon som har motivert innføring av 4-begrep signalsystem flere steder i utlandet.
Dette gjelder en situasjon hvor man (ofte etter oppgradering av infrastruktur) skal innføre tog med vesentlig høyere hastighet enn tidligere, mens det fortsatt skal gå mange tog med den tidligere toppfarten på strekningen (typiske hastigheter er 200 mot 140/160 km/h). For å tillate en slik hastighetsøkning må man normalt øke blokklengden betydelig, ofte til bortimot det dobbelte. Dette vil føre til vesentlig økte togfølgetider mellom de “langsomme” togene, og dermed redusert kapasitet.
Et godt alternativ er da å beholde blokkdelingen (og dermed signalplasseringen) og isteden innføre et 4. (høyere) begrep. De(n) opprinnelige togtypen(e) vil da betrakte de to høyeste begrepene som “kjør” og kan kjøre med samme togfølgetider som tidligere. Den raskeste togtypen kan imidlertid bare holde toppfart ved høyeste begrep. I tillegg til å være kapasitetsmessig fordelaktig vil en slik endring av signalsystemet ofte bli rimeligere enn nybygging hvis de opprinnelige signalene (og annet utstyr) fortsatt kan benyttes.
I dette tilfellet benyttes altså 4-begrep systemet ikke primært til kapasitetsøkning, men til å muliggjøre kjøring med høyere hastighet samtidig som kapasiteten beholdes ved kjøring med den opprinnelige topphastigheten.
Kapasitet på enkeltspor
Kapasitetsbetraktninger for enkeltspor blir ofte noe mer komplisert enn for dobbeltspor, og slike enkle uttrykk som er utledet for dobbeltspor, synes kanskje heller ikke like nyttige for enkeltspor. Problemstillingen man møter på enkeltsporede strekninger vil oftest være å finne de(t) tiltak som mest effektivt kan øke kapasiteten framfor å beregne den nøyaktige kapasitet for en gitt utforming.
Vi vil begynne med enkle (idealiserte) tilfeller før vi går til mer realistiske situasjoner.
Utseende av en typisk enkeltsporstrekning
Vi vil først gi en kort, skjematisk beskrivelse av hvordan en typisk enkeltsporet strekning ser ut ved JBV.
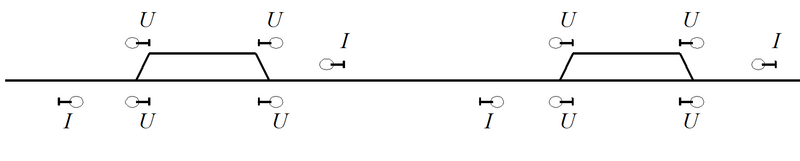
En enkeltsporstrekning består av stasjoner hvor togene kan møtes (“krysse”) og linjen mellom stasjonene. Følgende figur viser en skjematisk fremstilling av en stasjon og hovedsignalenes plassering.
Figur 16: Skjematisk framstilling av en stasjon og hovedsignalenes plassering.
Signalene som angir om et tog får tillatelse til å kjøre inn på stasjonen, kalles innkjørsignaler (I på figuren ovenfor). Disse markerer også stasjonsgrensen, dvs. skillet mellom stasjonen og linjen. Normal plassering er minst 200m utenfor ytterste sporveksel.
Signalene som gir et tog tillatelse til å forlate stasjonen og kjøre ut på strekningen til neste stasjon, kalles utkjørsignaler (U på figuren ovenfor). På tradisjonelle fjernstyrte stasjoner plasseres disse ved (eller noen få meter før) “middelpunktet”, dvs. det punkt hvor to tog på hvert sitt spor vil berøre hverandre. På stasjoner uten fjernstyring kan det være et felles utkjørsignal for alle spor som står rett utenfor ytterste sporveksel.
Strekningen mellom to stasjoner kan være delt i to av et signal, kalt blokkpost eller blokksignal. Dette muliggjør at det kan være to tog etter hverandre på strekningen mellom de to stasjonene, omtrent som på dobbeltspor. Dette gir økt kapasitet hvis det er behov for å kjøre flere tog i samme retning før det kommer et motgående tog.
Alle hovedsignalene på fjernstyrte strekninger har forsignaler plassert på normal forsignalavstand. Forsignalene for utkjørhovedsignalene plasseres normalt på samme mast som foregående innkjørhovedsignal. Stasjoner uten fjernstyring har oftest ikke forsignal for utkjørhovedsignalene.
For å få grønt (kjør) i et hovedsignal kreves det (bl.a.) at strekningen fram til neste hovedsignal er fri for tog. Når et signal viser grønt, kan man si at etterfølgende strekning (minst til neste hovedsignal) er reservert for det første toget som passerer det grønne signalet. En slik reservert strekning kalles en togveg. En blokkstrekning kan aldri inneholde mer enn ett tog eller en togveg om gangen.
For en stasjon som ikke er fjernstyrt (kalles stasjonsstyrt), gjelder følgende regel ved kryssing: Det andre toget skal ikke gis tillatelse til innkjøring før personalet har forvisset seg om at det første toget har stoppet.
Da fjernstyring ble innført, måtte denne regelen endres. Bestemmelsen er nå at det skal gå en viss tid fra det første toget er kommet helt inn på kryssingssporet (innenfor “middelpunktet”) til det andre toget kan få tillatelse til innkjør. Denne tiden kalles kryssingslåsetid (iblant forkortet x-låsetid). Størrelsen avhenger av sporets lengde, og den skal tilsvare noe mer enn normal kjøretid fra sporets begynnelse til toget har stoppet. Ved JBV er denne tiden 50 - 70 sekunder avhengig av sporlengden.
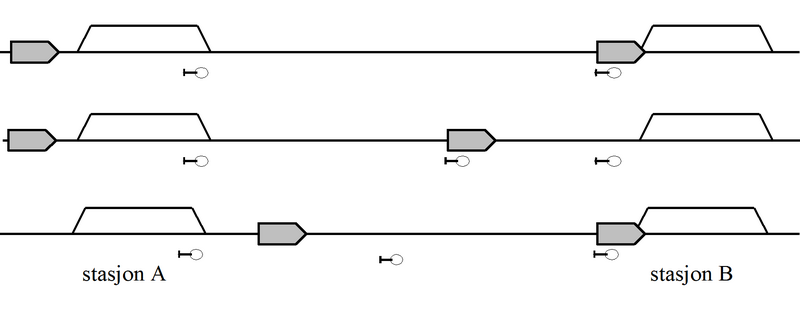
Som vi skal se senere i dette kapitlet, fører denne bestemmelsen til at en kryssing tar ganske lang tid. En mer effektiv stasjonsutforming er en som tillater begge tog å kjøre inn uavhengig av hverandre. Innkjørtogvegene kan da legges fra begge sider samtidig. En slik utforming kalles samtidig innkjøring og er vanlig i mange andre land. Stasjonen må da ha en utforming som hindrer kollisjon selv om et av togene skulle gli noe forbi utkjørhovedsignalet. Dette gjøres ved en sikkerhetssone mellom utkjørhovedsignalet og middelpunktet eller ved sporveksler til et buttspor bak utkjørhovedsignalet. JBV har foreløpig kun et fåtall slike stasjoner, men nye stasjoner bygges nå hovedsaklig av denne type.
I det følgende vil vi ofte bruke begrepet kryssingsspor (x-spor) som er en driftsteknisk betegnelse som ofte brukes om 2- eller få-spors stasjoner.
Dimensjonerende strekningsavsnitt og teoretisk kontra praktisk kapasitet
Dimensjonerende strekningsavsnitt ble også omtalt under dobbeltspor i kap. 2.4 som strekningsavsnittet med lavest kapasitet.
På enkeltspor vil vi bruke betegnelsen strekningsavsnitt om enhver strekning mellom to etterfølgende stasjoner (inkl. stasjonene). Figuren i forrige avsnitt viser altså et helt strekningsavsnitt og deler av to andre.
Det dimensjonerende strekningsavsnitt er fortsatt det strekningsavsnitt med lavest kapasitet innen strekningen vi ser på. Dette begrepet blir mer sentralt for enkeltspor enn for dobbeltspor fordi det nesten aldri er aktuelt å beregne kapasiteten for en enkeltsporstrekning uten mellomliggende stasjoner.
Det blir dermed også viktigere å få med antall strekningsavsnitt eller totalstrekningens lengde når man skal anslå den praktiske kapasitet.
I UIC-kodex 405E (ref. / 1 /) har man sammen med erfaringstall for buffertid (kapasitetsutnyttelse) som omtalt i kap. 2.3, også anført erfaringstall for å ta hensyn til antall strekningsavsnitt. Dette er gjort i form av et tillegg til midlere togfølgetid og buffertid. Den praktiske kapasitet blir da uttrykt
der tt er tilleggstiden som er satt proporsjonal med antall strekningsavsnitt. Som erfaringstall anføres at man kan sette
min.
der a er antall strekningsavsnitt.
Bruk av dette enkle uttrykk for tilleggstiden forutsetter at det er noenlunde jevn tidsmessig avstand mellom kryssingssporene.
På mange norske strekninger er situasjonen slik at bygging av et nytt kryssingsspor på den dimensjonerende delstrekning gir ingen eller liten økning i kapasiteten i følge denne formelen. Dette er en indikasjon på at strekningen er kapasitetsmessig balansert, dvs. at det ikke er noen markerte flaskehalser (i følge denne enkle måte å se det på).
Idealisert tilfelle
Vi ser først på et idealisert tilfelle hvor kryssingssporene er så lange at togene kan krysse ved full hastighet og hvor det ikke er noen signalmessige avhengigheter mellom innkjørtogvegene. Dette vil ofte bli betraktet som dobbeltsporede seksjoner på en (i hovedsak) enkeltsporet strekning.
Den viktigste faktoren for kapasiteten i en slik situasjon er selvsagt kjøretiden over det dimensjonerende strekningsavsnittet på strekningen. Hvis vi gir denne kjøretiden en noe utvidet omfang/betydning, blir det den eneste parameteren når dimensjonerende strekningsavsnitt ikke har blokksignaler. Kjøretiden må da regnes fra forsignalet for utkjørsignalet på den ene stasjonen til hele toget er inne på neste stasjon.
Dermed blir togfølgetiden (t) identisk med kjøretiden over strekningsavsnittet. (Vi har da vært litt upresise med definisjonen av togfølgetid: den refererer ikke noe bestemt sted på strekningen. Under behandlingen av ordinære stasjoner i neste avsnitt gjøres det grundigere.)
Hvis alle tog har tilnærmet lik kjøretid over det dimensjonerende strekningsavsnitt, blir den teoretisk kapasitet over tidsrommet T ganske enkelt
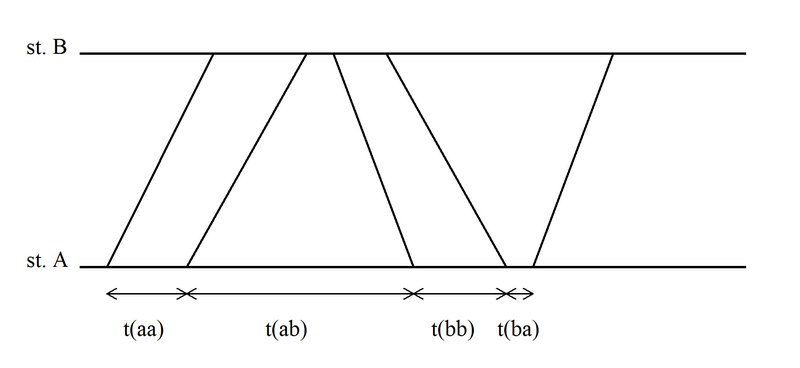
På følgende figur er vist maksimal utnyttelse (teoretisk kapasitet) av et dimensjonerende strekningsavsnitt, som ikke har blokksignaler, i et tilfelle med to togslag med ulike kjøretider.
Figur 17: Maksimalt tett trafikk over et strekningsavsnitt med idealiserte stasjoner.
I en slik situasjon må vi beregne den midlere togfølgetid (eller midlere kjøretid i dette idealiserte tilfelle). Dette gjøres ved en veid sum på liknende måte som for blandet trafikk på dobbeltspor, omhandlet i kap. 2.2.
Vi deler da togene inn i klasser eller grupper med lik eller tilnærmet lik kjøretid. Det trengs nå togfølgetider for alle de kombinasjoner av togfølger som finnes i ruteplanen. I dette svært forenklede tilfelle er, som tidligere nevnt, togfølgetiden lik kjøretiden for det første toget, og altså uavhengig av det andre toget. Man trenger ikke en fullstendig ruteplan, men man må ha rekkefølgen av tog fra de ulike grupperinger. Man teller opp antall tilfeller av de ulike kombinasjoner og beregner en midlere togfølgetid:
Her betyr
ni : antall togfølgetider hvor et tog fra gruppe i er først
ti : minste togfølgetid når et tog fra gruppe i er først (= kjøretiden for tog fra gruppe i)
Summen tas over alle tog-grupper. Opptellingen av tilfeller gjøres for et tidsrom av tilstrekkelig lengde til å få med alle aktuelle situasjoner.
Deretter beregnes den teoretiske kapasiteten som før:
Uten blokksignaler på det dimensjonerende strekningsavsnittet blir togfølgetiden tilnærmet den samme uavhengig av hvilken retning det andre toget kjører i. Ved innføring av et blokksignal midt på det dimensjonerende strekningsavsnittet, vil togfølgetiden for to tog i samme retning tilnærmet halveres, og kapasiteten på dette strekningsavsnittet øker med økende puljekjøring på liknende måte som ved blandet trafikk på dobbeltspor (kap. 2.2.3). Det er særlig på strekninger hvor det på visse deler av dagen er hovedsaklig ensrettet trafikk (rushtider) at dette kan komme til praktisk nytte.
Ved slik å øke kapasiteten på det dimensjonerende strekningsavsnitt vil man vanligvis raskt komme i den situasjon at et annet strekningsavsnitt har lavere kapasitet og således blir dimensjonerende. For eventuelt ytterligere å øke kapasiteten må tiltak settes inn på det nye dimensjonerende strekningsavsnitt.
Mer en ett blokksignal mellom to stasjoner på enkeltspor er ytterst sjelden aktuelt.
Med flere togslag med ulik hastighet og stoppmønster kan det være ett strekningsavsnitt som har lengst kjøretid for et togslag, mens det kan være et annet for det andre togslaget. Bruk av blokksignaler og noe puljekjøring kan også medvirke til at det strekningsavsnittet med lengst kjøretid ikke er dimensjonerende likevel. I slike situasjoner er det nødvendig å gjennomføre kapasitetsberegningen for alle potensielt dimensjonerende strekningsavsnitt.
Fra denne helt enkle formuleringen ser man også at redusert kjøretid direkte slår ut på kapasiteten (i tillegg til at det å redusere kjøretiden i seg selv er meget viktig). Dette gir spesielt stor virkning ved oppgradering av strekninger der linjehastigheten er lavere enn maksimalhastigheten for langsomste togtype da man i slike situasjoner får redusert kjøretid for alle tog. På omtrent alle norske strekninger er det mange hastighetsavsnitt hvor selv godstog ikke kan holde sin toppfart. Ved oppgradering til vesentlig høyere hastigheter enn nåværende maksimalhastighet må kapasitetsmessig virkning av økt forsignalavstand også medtas, samt konsekvenser av eventuell økt differanse i hastighet mellom ulike togslag. Når det nå planlegges hastighetsmessig oppgradering av mange strekninger i Norge, er det viktig å få med at dette også betyr økt kapasitet.
Når man vurderer økt hastighet (redusert kjøretid) på en hel banestrekning, vil man se denne kapasitetsøkningen f.eks. ved at hvert tog møter færre motgående tog fordi det er ute på strekningen en kortere tid enn før. Man kan dermed øke frekvensen uten at strekningen belastes hardere kapasitetsmessig.
For enkeltsporede strekninger er det altså som hovedregel slik at økt linjehastighet medfører økt kapasitet, mens det for dobbeltspor normalt er slik at økt linjehastighet medfører redusert kapasitet (jfr. beregningene av optimal kapasitet på dobbeltspor).
Det som ovenfor er sagt, gjelder ved hastighetsøkninger som får konsekvenser for alle tog. En helt annen situasjon er det hvis man skal sprenge inn noen få hurtigere tog mellom mange langsomme tog. En slik situasjon vil kreve en mer omfattende vurdering.
Fullstendig kapasitetsberegning etter UIC 405E
Vi går nå over til å se på en mer reell situasjon med ordinære stasjoner slik som det ble beskrevet i begynnelsen av dette kapitlet. Det er da mer omstendelig å beregne togfølgetider, og det blir flere ulike tilfeller som må behandles. Vi vil her gi en forenklet gjengivelse av framstillingen i UIC 405E anvendt på dette tilfellet.
Utover økt detaljering og nøyaktighet er hovedforskjellen fra forrige avsnitt at det tas hensyn til tidsforbruket som skyldes avhengigheten mellom innkjørtogveiene på ordinære stasjoner. Dette krever tilgang til en mer detaljert ruteplan enn bare rekkefølgen mellom ulike togtyper som vi tidligere har klart oss med.
Midlere togfølgetid
Vi ser da på et strekningsavsnitt hvor vi kaller stasjonene i hver ende for h.h.v. A og B. Videre lar vi a betegne kjøreretningen fra stasjon A til B, og b betegner motsatt retning. Selv med bare en togtype, får vi da fire ulike slag av togfølger; disse kan da benevnes med aa, ab, ba og bb hvor første bokstav betegner kjøreretningen for det første toget og den andre bokstaven for det andre toget. Den midlere togfølgetid over strekningsavsnittet når vi bare har en togtype, blir da
hvor betydningen er
n(xy) : antall togfølgetilfeller med et tog i retning x før et i retning y
t(xy) : togfølgetiden for et tog i retning x før et i retning y
Med flere togtyper må vi som før gruppere togene i grupper med tilnærmet like egenskaper, i denne situasjonen vil egenskaper stort sett bety kjøretid mellom stasjonene A og B. Det må beregnes togfølgetider for alle kombinasjoner som fins i ruteplanen. Man teller opp antall tilfeller av de ulike kombinasjoner og beregner en midlere togfølgetid ved
Her er
nij(xy) : antall togfølgetilfeller med et “i-tog” i retning x før et “j-tog” i retning y
tij(xy) : togfølgetiden for et “i-tog” i retning x før et “j-tog” i retning y
I situasjoner hvor det ikke er opplagt hvilket strekningsavsnitt som er dimensjonerende, må midlere togfølgetid beregnes på denne måten for alle strekningsavsnitt som kan tenkes å være dimensjonerende. Deretter kan man beregne den teoretiske og praktiske kapasitet på samme måte som før, ved hjelp av midlere togfølgetid for det dimensjonerende avsnitt.
Formelen ovenfor kan sammenliknes med formelen i kap. 2.2.1, og vi ser at regnearbeidet er minst firedoblet for enkeltspor.
Vi skal så gå noe inn på beregning av togfølgetider for de fire tilfellene.
Vi vil relatere togfølgetidene til stasjon A. Dette medfører at t(ab) blir stor og t(ba) liten som vist på følgende figur. Hvis man tar utgangspunkt i stasjon B, blir dette motsatt, men den resulterende kapasitet blir selvsagt den samme. Følgende figur viser et eksempel på de 4 ulike togfølgetilfellene.
Figur 18: De fire ulike togfølgetilfellene ved enkeltsporet drift.
I det følgende skal vi gå nærmere inn på beregning av disse ulike togfølgetilfellene.
Togfølgetid ved kjøring i samme retning
Beregningen av togfølgetidene for to tog i samme retning, dvs. t(aa) og t(bb), blir som for dobbeltspor. Følgende figur viser de aktuelle tilfeller. Figuren viser kun hovedsignaler, ikke forsignaler.
Figur 19: Togfølgetider ved kjøring i samme retning på enkeltspor: øverst: stasjoner uten mellomliggende blokkpost, midten: blokkpost, avstanden fra st. A til blokkpost er dimensjonerende, nederst: blokkpost, avstanden fra blokkpost til st. B er dimensjonerende.
Hvis ingen av togene stopper på noen av stasjonene (eller mellom dem) og hastigheten (v) antas konstant, kan togfølgetiden i disse tilfellene uttrykkes
Her betegner som før L toglengde (for første tog) og ts siktavstand (tidsmessig). Videre er bf forsignalavstanden foran det bakerste signalet (signalet foran tog 2), og bl betegner blokklengden på linjen. I tilfellet uten blokkpost er den sistnevnte avstanden fra utkjør til neste stasjons innkjør. I tilfellene med blokkpost er den enten avstanden utkjør til blokkpost eller blokkpost til innkjør.
Ved stopp ute på linjen må uttrykket økes med leddene (v/r) + (v/a) + to for hvert stopp slik som for dobbeltspor (kap. 3.3.2). Hvis tog 2 har rutemessig stopp på stasjon A, erstattes (bf / v) + ts av reaksjonstid ved avgang fra stasjon, samt tidstillegg for akselerasjon.
For enkeltspor vil man ofte bruke de rutemessige kjøretidene mellom stasjonene for å finne togfølgetidene. Man må da legge til et anslag for (L + bf) / v + ts.
Normalt er bf av størrelsesorden v2/r, mens bl er betydelig større. Togfølgetidene for to tog i samme retning er derfor normalt mye større for enkeltspor enn for dobbeltspor. Selvfølgelig er det teknisk mulig å signalere et enkeltspor slik at togfølgetiden for to tog i samme retning blir like lav som på et dobbeltspor, men dette er sjelden aktuelt i praksis.
Togfølgetid ved bytte av retning
Ved beregning av togfølgetiden for to tog i hver sin retning, må vi også ta med tidsforbruket ved kryssingen. Togfølgetidene referert stasjon A kan da uttrykkes
hvor
ta er kjøretiden for tog 1 fra stasjon A til B
tb er kjøretiden for tog 2 fra stasjon B til A
tk,X er tidsforbruket ved kryssing på stasjon X.
Kjøretidene ta og tb avhenger av avstanden mellom stasjonene, linjehastigheten og togenes egenskaper. Vi går for øvrig ikke nærmere inn på beregning av disse kjøretidene da de hovedsaklig kan hentes fra ruteplanen.
Tidsforbruket ved kryssingen avhenger av stasjonens utforming og av den tidsmessige forskjellen mellom togenes ankomst til stasjonen. For ordinære stasjoner (med kryssingslåsetid) er den gunstigste situasjonen at det andre toget er like foran (dvs. på siktavstand til) forsignalet for innkjør i det kryssingslåsetiden utløper. I denne situasjonen er tidsforbruket ved kryssingen minst, og denne situasjonen brukes derfor ved kapasitetsberegningen. I kap. 4.5 behandles tidsforbruket ved en kryssing mer i detalj.
I UIC 405E brukes to ulike formler for tidsforbruket ved en kryssing, avhengig av om det andre toget skal stoppe på den stasjonen som innleder strekningsavsnittet eller ikke.
Når tog 2 skal passere stasjonen det krysses på, må tog 1 komme inn på stasjonen og kryssingslåsetiden utgå før tog 2 er på siktavstand til FS innkjør, dvs
der
tx kalles togvegleggingstid, utløsetid, blokkbetjeningstid
tiu er kjøretiden fra innkjør forsignal til utkjør hovedsignal
ts er siktavstanden (i tid)
Når tog 2 også skal stoppe på kryssingsstasjonen, angis
tk = tx + “avgivelse og opptagelse av avgangssignal”
tx avhenger sterkt av stasjonsutformingen: ordinær stasjon med kryssingslåsing eller stasjon som tillater samtidig innkjøring. For ordinære stasjoner vil denne tiden videre avhenge sterkt av hvilket tog som i ruteplanen kjører først inn på kryssingsstasjonen. Når tog 1 kjører først inn på kryssingssporet, kommer kryssingslåsetiden (50 - 70s) med i tx og er det dominerende ledd. Når tog 2 kjører først inn på kryssingssporet, blir tx nærmest neglisjerbar på fjernstyrte stasjoner med magasinert togveg (den vanligste situasjonen).
Tiden til “avgivelse og opptagelse av avgangssignal” kan bli merkbar på større stasjoner med manuelt avgangssignal (fra togekspeditør til togfører), men for ordinære fjernstyrte kryssingsspor blir dette et nærmest neglisjerbart ledd (som typisk verdi for norske forhold kan antydes 5s for tog uten passasjerutveksling og 15s med passasjerutveksling).
Virkning av samtidig innkjøring på stasjoner
Som tidligere nevnt, kan stasjoner som tillater samtidig innkjøring, avvikle kryssinger med vesentlig mindre tidstap enn ordinære stasjoner. For å kunne se virkningen av denne mer effektive stasjonsutformingen på beregningene i det foregående, gjør vi en del forenklinger: Vi ser på det enkleste tilfelle med lik kjøretid for alle tog i begge retninger (ta = tb) og annet hvert tog i hver sin retning, dvs. n(aa) = n(bb) = 0 og n(ab) = n(ba). Videre forutsetter vi at begge stasjonene er like, og at tog 1 kjører først inn på kryssingssporet i halvparten av kryssingene på de to stasjonene. Vi neglisjerer også tiden til “avgivelse og opptagelse av avgangssignal” (dvs. tk er tilnærmet null i halvparten av tilfellene). Da får vi
hvor tk kun betegner den fulle verdien som typisk settes til ca. 3 min. i ruteplanen for en kryssing mellom to persontog på en ordinær stasjon. For en stasjon med samtidig innkjør er tidstapet tilnærmet null hvis begge tog har rutemessig stopp, mens det for passerende tog kan antydes ca 0.5 min. (tidstillegg pga. retardasjon og akselerasjon).
For tilfellet med to stoppende tog blir den teoretiske kapasiteten med ordinære stasjoner
,
mens det med samtidig innkjøring blir
Som vi ser er kapasitetsgevinsten ved overgang til stasjoner med samtidig innkjør større jo kortere kjøretiden mellom stasjonene er.
Eksempel: Vi skal anslå kapasitetsøkningen ved overgang til stasjoner med samtidig innkjøring ved å benytte de samme tilnærmelsene som ovenfor. Vi setter da kjøretiden mellom stasjonene til 6 min. som er rimelig representativt for JBVs nærtrafikkstrekninger og også for deler av IC-strekningene. Tidstapet ved kryssing på en ordinær stasjon settes vanligvis til 3 min. Den teoretiske maksimalkapasiteten uten samtidig innkjøring blir da
[tog/time],
mens vi med samtidig innkjøring får
[tog/time]
Med erfaringstallene fra UIC 405E og hvis antall strekningsavsnitt settes til 8 i dette eksempelet, får vi for den praktiske kapasitet uten samtidig innkjøring
[tog/time]
Tilsvarende får vi med samtidig innkjøring
[tog/time]
Selv om det her er gjort mange forenklinger, er disse forholdsvis nær vanlig forekommende situasjoner, og resultatene burde derfor være rimelig representative.
Mer detaljert framstilling av tidsforbruket ved en kryssing
Vi vil i dette avsnittet beskrive tidsforbruket ved kryssing mer i detalj for et ordinært kryssingsspor og for et som tillater samtidig innkjør. Det virkelige tidsforbruket ved en kryssing sammenliknet med situasjonen på dobbeltspor vil her komme tydeligere fram. Likeledes vil man se fordeler ved samtidig innkjør ut over bortfall av x-låsetiden.
Fremstillingen her bygger på ref. / 4 / som omhandler tidsgevinsten ved samtidig innkjøring. Beregningene der gjelder Asper stasjon, som ligger omtrent midt mellom Kløfta og Jessheim stasjoner, på strekningen Lillestrøm - Eidsvoll. Asper er JBVs (NSBs) første 2-spors kryssingsspor med samtidig innkjør, tatt i bruk i 1984. Figurene i dette avsnittet er hentet fra samme artikkel.
De fleste beregningene her er gjort for NSBs vanlige nærtrafikktog (type 69). Først vises et detaljert tid-veg diagram over hvordan en kryssing forløper ved ordinær utforming (med kryssingslåsing) og ved samtidig innkjør.
Figur 20: Tid-veg diagram for kryssing mellom to nærtrafikktog uten rutemessig stopp.
I den viste situasjonen ankommer togene omtrent samtidig til kryssingsstasjonen (Asper på figuren). Med ordinær utforming av denne påføres begge tog et betydelig tidstap (2 - 3 min. pr. tog) sammenliknet med situasjonen uten kryssing eller i forhold til dobbeltspor. Det samlede tidsforbruket er omtrent det samme som hvis kryssingen hadde skjedd på en av nabostasjonene (kryssing på Jessheim er vist på figuren). Hvis derimot kryssingsstasjonen tillater samtidig innkjøring, blir tidstapet bare ca. 0.5 min. pr. tog (og kunne vært redusert ytterligere ved bruk av repeterbaliser for ATS-systemet). Det er i denne situasjonen (to tog samtidig klar til avgang fra hver sin stasjon) at man forventer størst nytte av et nytt kryssingsspor mellom disse stasjonene, men det er også i denne situasjonen at tidsforbruket ved kryssing er størst for en tradisjonell stasjon. Dette skyldes at togene kommer samtidig til kryssingsstasjonen, mens det optimale er en differanse på 2 - 4 min. (avhengig av togslag).
Den forrige figuren viser tidsforløpet for en spesifikk situasjon: begge tog starter samtidig fra nabostasjonene på hver side av kryssingsstasjonen. For å få en oversikt over det samlede tidsforbruket for begge tog i alle situasjoner må tidsforbruket beregnes for ulike situasjoner når det gjelder starttid. Et eksempel på dette er vist i neste figur. Differansen mellom tidspunktet når det ene toget starter fra nabostasjonen i nord (Jessheim på figurene) og tidspunktet når det andre toget starter fra nabostasjonen i syd (Kløfta på figurene) kaller vi for starttidsforskyvningen (Δt). Foregående figur viser altså det detaljerte kryssingsforløp når Δt = 0. Starttidsforskyvningen angir også hvor på strekningen togene ville møtes hvis det var dobbeltspor. (Med strekningen menes den totale strekningen vi her ser på; Kløfta - Jessheim på figurene.) På neste figur vises det samlede tidsforbruket for de to togene som funksjon av starttidsforskyvningen.
Figur 21: Samlet tidsforbruk (T) som funksjon av starttidsforskyvningen (Δt) for to nærtrafikktog uten rutemessig stopp.
Denne figuren er egentlig sammensatt av to deler. I høyre halvdel vises forløpet av samlet tidsforbruk (T) som funksjon av starttidsforskyvningen (Δt) for følgende tilfeller:
- kryssing på Jessheim (strek-punktert linje)
- tradisjonell kryssing på Asper hvor toget fra Kløfta kjører først inn og i avvik (heltrukken linje)
- kryssing med samtidig innkjør på Asper hvor toget fra Kløfta kjører i avvik (stiplet linje).
Disse kurvene er ført noe over i venstre halvdel av diagrammet for å vise hvordan tidsforbruket blir hvis denne signalering og sporbruk beholdes når bytting av togrekkefølge og sporbruk ville gitt et raskere forløp.
I venstre halvdel av figuren vises på samme måte kurvene for:
- kryssing på Kløfta
- tradisjonell kryssing på Asper hvor toget fra Jessheim kjører først inn og i avvik
- kryssing med samtidig innkjør på Asper hvor toget fra Jessheim kjører i avvik.
Som referanse vises også tidsforbruket ved dobbeltspor (heltrukken linje).
Av et slikt diagram ser man tidsforbruket for ulike stasjonsutforminger, og de kan sammenliknes med tidsforbruket ved dobbeltspor og ved kryssing på nabostasjon.
For det konkrete tilfellet som figurene her er hentet fra, ser man at bygging av et nytt kryssingsspor (Asper) gir praktisk talt ingen tidsgevinst hvis det utformes på tradisjonell måte (med kryssingslåsing). Dette skyldes at avstanden mellom de opprinnelige stasjonene her er så kort at det samlede tidsforbruket ved kryssingen kan bli omtrent like stort som kjøretiden over den opprinnelige strekningen (uten det nye kryssingssporet). Hva slags utbyggingstiltak som gir best effekt i ulike situasjoner, omtales noe mer i kap. 4.7.
I ref. / 4 / vises også tilsvarende figurer for kryssing mellom to nærtrafikktog med stopp på strekningen og for to godstog. Dessuten gis en mer detaljert forklaring av hvorfor de ulike kurvene ser ut som de gjør.
En stasjonsutforming som tillater samtidig innkjøring, har også enkelte andre positive virkninger, bl.a. blir det noe enklere for toglederne å treffe optimale beslutninger. Også dette omtales nærmere i nevnte artikkel.
Effekt av stive ruter
Ved bruk av stive ruter (dvs. avganger på faste minutt-tall) på enkeltspor vil kryssinger mellom de tog som har faste ruter opptre på de samme stasjoner i hver “syklus”. Disse stasjonene får da vesentlig flere kryssinger enn de øvrige på strekningen. Hvis alle togene på strekningen har stive ruter, får de faste kryssingspunktene alle kryssingene rutemessig, og de øvrige kryssingsspor blir bare brukt ved omlegging av kryssinger pga. forsinkelser.
I slike situasjoner med faste kryssingspunkter er det viktig at kryssingene kan avvikles mest mulig effektivt på disse stasjonene, og disse bør derfor ofte bygges ut til en høyere standard enn de øvrige hvis det faste mønster forventes beholdt i mange år framover.
En slik utbygging av de faste kryssingspunktene har vanligvis en stor betydning for punktligheten på strekningen. Men skjematiske beregninger som med UIC 405E tar ikke hensyn til slike faste kryssingspunkter som framkommer ved stive ruter.
Kapasitetsforbedring på slike faste kryssingspunkter kan ha vesentlig bedre virkning på punktligheten enn den formelle kapasitetsøkningen skulle tilsi. Virkningen kommer bedre fram ved å se detaljert på tidsforbruket på de faste kryssingspunktene slik som vist i forrige avsnitt eller ved bruk av simuleringsmodeller for hele strekningen.
Kapasitetsøkende tiltak på enkeltspor
Vi vil her gi en kort gjennomgang av aktuelle kapasitetsøkende tiltak på enkeltspor. Kun banetekniske tiltak blir omtalt.
De banetekniske tiltak som er aktuelle for å øke kapasiteten på en enkeltsporet strekning, kan grovt grupperes i tre:
- nye kryssingsspor
- forbedret utforming av kryssingssporene
- økt hastighet
Den første spørsmålsstillingen man bør se på er om det bør bygges nye kryssingsspor eller om man bør effektivisere de man har. Jo lengre kjøretid det er mellom stasjonene, desto større nytte får man av nye kryssingsspor. Jo kortere kjøretid det er mellom stasjonene, desto større nytte får man av effektivisering av de eksisterende stasjonene. For et konkret tilfelle må man se på nytte og kostnad ved de ulike alternativene. Som en grov hovedregel for JBVs strekninger kan man si at på nærtrafikk- og intercity-strekninger vil forbedring av de eksisterende kryssingssporene være mest fordelaktig. Bygging av nye stasjoner av tradisjonell type (uten samtidig innkjør) vil bare være aktuelt på de svakest trafikkerte strekningene.
Et annet alternativ for å redusere den tidsmessige avstanden mellom kryssingssporene er økt hastighet. Mange steder i Norge er det også muligheter for direkte innkorting av linjen mellom to stasjoner i tillegg til hastighetsøkning. Ut fra en isolert kapasitetsmessig betraktning vil økt hastighet sjelden kunne konkurrere med nye kryssingsspor eller ombygging av de eksisterende. Men som et kombinert tiltak som både gir reduserte (netto) kjøretider og økt kapasitet, vil det mange steder være aktuelt.
De forhold ved stasjonsutformingen som har kapasitetsmessig betydning er:
- samtidig innkjøring
- sporveksler som tillater høyere hastighet i avvik
- sporlengde
Av disse er samtidig innkjøring det klart viktigste.
Når en stasjon tillater samtidig innkjør, øker effektiviteten (= reduseres tidstapet ved kryssingen) med økende sporlengde (forutsatt at signalering og sporvekslenes standard “følger med”). For en stasjon med kryssingslåsing betyr økt sporlengde bare at lange godstog kan krysse også på denne stasjonen, men for korte tog blir det ingen forbedring; tvert imot kan man risikere at tidsforbruket ved kryssingen øker fordi kryssingslåsingstiden økes hvis sporforlengelsen er betydelig.
Sporvekslenes maksimale hastighet (i avvik) bør normalt økes med økende sporlengde og med økende antall kryssinger. Men det er sjelden aktuelt å gå opp til linjehastighet.
Hvis et kryssingsspor er så langt at det er aktuelt å dele det i to blokkstrekninger (lengde minst to bremselengder for dimensjonerende tog) og praktisere “alltid høyrekjøring” vil man ofte bruke betegnelsen dobbeltsporet seksjon istedenfor kryssingsspor. Ved en slik utforming kan to tog i prinsippet (dvs. ved samtidig ankomst) krysse uten annen hastighetsreduksjon enn den som skyldes avvikende sporveksel.
For utbygging av en konkret strekning må nytte og kostnad for ulike tiltak vurderes. Det kan ikke sies så mye generelt om hvilke tiltak som er mest kostnadseffektive utover et par momenter:
- På alle tett trafikkerte strekninger bør ombygging av stasjonene til samtidig innkjøring vurderes. Dette vil ofte være et av de mest kostnadseffektive tiltak.
- Det vil normalt lønne seg å bygge ut eventuelle faste kryssingspunkter først og ofte til en høyere standard enn øvrige kryssingsspor. Man må i den sammenheng være klar over at ved fremtidig hastighetsøkning på en strekning med stive ruter flytter de faste kryssingspunktene seg. Man bør derfor vurdere framtidige ruteopplegg, materielltyper og hastighetsøkninger før man går til en omfattende utbygging av faste kryssingspunkter.
Togenes punktlighet
Kapasitetsmessige konsekvenser av tekniske feil
Vi skal her se hvordan ulike tekniske feil - på materiell eller infrastruktur - påvirker en streknings kapasitet. Betraktningene vil hovedsaklig være kvalitative eller med henvisning til tidligere omtalte metoder. Vi tar for oss en strekning med en start- og en sluttstasjon, men togene kan eventuelt trafikkere en lengre strekning enn den vi ser på.
Forsinkelser som oppstår på eller før den første stasjonen på den strekningen vi betrakter, fører ikke til redusert kapasitet på denne strekningen fordi de øvrige togene kan gå uavhengig av det forsinkede toget. Riktignok vil det forsinkede toget - når det går ut på strekningen - normalt føre til forsinkelse også for andre tog; dette skal vi behandle i kap. 5.2.4.
Vi skal her se litt nærmere på ulike typer tekniske feil som kan oppstå underveis på den strekningen vi betrakter.
Vi ser først på feil ved materiellet (toget) som vi grovt vil gruppere i tre kategorier:
- Kortvarig feil.Vi tenker her på en feil som kan rettes på stedet, uten at det går så lang tid at man setter i gang omdisponeringer som forbikjøring o.l.
- Varig feil, men toget kan kjøre videre.Dette gjelder feil som redusert trekk-kraft (en motor ute av bruk), redusert toppfart o.l.
- Langvarig feil, toget kan ikke kjøre. Dette medfører at sporet som toget står på, ikke kan brukes før feilen er rettet eller toget fjernet. Konsekvensene blir da de samme som om sporet er ute av bruk pga. feil i infrastruktur, punkt b) eller c) nedenfor.
For feil ved infrastrukturen har vi også gjort en liknende gruppering i tre kategorier:
- Kortvarig feil. Dette gjelder også feil som ikke varer så lenge at man setter i gang omdisponeringer som forbikjøring o.l. Det kan dreie seg om feil som kan utbedres av togpersonalet eller feil som bare viser seg nå og da (f.eks. kortvarig signalfall, manglende kontroll på sporveksler).
- Varig redusert kapasitet. Det tenkes her på en situasjon som varer lenge, men feilen er ikke slik at strekningen er blokkert. Det kan dreie seg om saktekjøringer, et kryssingsspor som ikke kan brukes, eller et spor ute av bruk på strekninger med flere spor.
- Total stopp av trafikk. Alle spor på en strekning er sperret slik at trafikken opphører inntil feilen er rettet.
Det som ovenfor er kalt kortvarig feil, er feil som primært bare rammer ett tog, men som så forplanter seg til andre tog (sekundære forsinkelser). Denne situasjonen behandles matematisk i kap. 5.2 (forsinkelsesforplantning).
Situasjonen med total stopp av trafikk tilsvarer jo at kapasiteten er null, og det er derfor ikke aktuelt å studere kapasiteten nærmere i denne situasjonen.
Det gjenstår da et mangfold av situasjoner med redusert kapasitet hvor man kan utføre kapasitetsberegninger. Disse omfatter punkt b) under materiell og punkt b) under infrastruktur (som også inkluderer deler av punkt c) under materiell). Vi skal her omtale endel av disse situasjonene litt nøyere:
- Varig materiell-feil, men toget kan kjøre videre. På JBVs dobbeltsporstrekninger, som er så korte, vil det normalt ikke foretas forbikjøringer selv om et tog går saktere enn det skulle. Dermed vil også dette tilfellet kunne dekkes av teorien for forsinkelsesforplantning. Dette vil også til en viss grad gjelde for enkeltsporstrekninger.
Det kan alternativt gjøres en kapasitetsberegning hvor det langsommere toget behandles som en egen tog-gruppe. Ved de samme metoder som omtalt i de foregående kapitler, vil man da få et tallmessig uttrykk for den reduserte kapasiteten.
- Saktekjøring for alle tog over en del av strekningen man ser på. Dette kan skyldes banemessige svakheter (solslyng f.eks.), problemer med signalanlegget som medfører at togene må få telefonisk ordre om å passere signal i stopp (det må da kjøres i max 40 km/h til neste signal), eller vedlikeholdsarbeid.
Som påvist i kap. 3.5, fører saktekjøring alltid til redusert togfølgetid på det aktuelle sted. For dobbeltspor fører dette normalt også til redusert togfølgetid over strekningen som helhet. For enkeltspor fører saktekjøring normalt til at dette strekningsavsnitt blir dimensjonerende. I begge tilfeller kan metodene i det foregående benyttes til å beregne kapasiteten i denne situasjonen med saktekjøring slik at man kan tallfeste reduksjonen i kapasitet. For situasjonen med kjøring på telefonisk ordre fra togleder må det også tillegges en betydelig tid for “avgivelse og opptak av avgangssignal”.
- Et kryssingsspor ute av bruk. Vi tenker her på en situasjon hvor bare ett spor på stasjonen kan brukes. Dette kan skyldes at en sporveksel ikke kan legges over, et spor ute av bruk pga. feil, vedlikehold o.a. Det kan altså ikke utføres kryssinger på denne stasjonen.
Hvis totalstrekningen vi ser på, er noenlunde kapasitetsmessig balansert, fører dette til at lengden av dimensjonerende strekningsavsnitt blir bortimot fordoblet, og den teoretiske maksimalkapasiteten blir bortimot halvert. Dersom det er stor forskjell mellom de ulike strekningsavsnitt, blir kapasitetsreduksjonen ved en slik feil mindre (hvis ikke kryssingssporet som er ute av bruk, i utgangspunktet lå inntil dimensjonerende strekningsavsnitt). Reduksjonen i den praktiske kapasitet blir noe mindre fordi antallet strekningsavsnitt da inngår i beregningen.
Med mindre kapasitetsutnyttelsen i utgangspunktet var forholdsvis lav (under 50%), vil en slik feil føre til at forsinkelsene stadig øker etter som tiden går. Det vil da bli en “kø” av tog på hver side av flaskehalsen. Dette medfører vanligvis økende puljekjøring, noe som igjen hever kapasiteten en del, slik at forsinkelsen pr. tog stabiliseres.
- Redusert sporantall på flerspors strekninger. Ved dobbeltspor fører blokkering av et spor til at man får trafikk i begge retninger på det gjenværende sporet, altså en enkeltsporet seksjon med dobbeltspor på begge sider. På strekninger med mer enn to spor fører blokkering av et spor normalt til at man får blandet trafikk i samme retning på et av de gjenværende spor, mens det tidligere var (mer) ensartet trafikk på dette sporet. I begge tilfeller får man en dramatisk kapasitetsreduksjon for totalstrekningen (alle spor sett under ett). Denne kan beregnes ved å beregne kapasiteten for den delstrekningen som utgjør flaskehalsen. Også i disse situasjonene vil det ofte bli en kø av tog på hver side av flaskehalsen, slik at man får en økende grad av puljekjøring og dermed noe høyere kapasitet.
For dobbeltspor vil vi også nevne de viktigste faktorene for kapasiteten når ett spor er sperret:
- lengden av den enkeltsporede seksjonen, dvs. avstanden mellom to sporsløyfer; denne må inkludere vekselsonene fra siste signal før den enkeltsporede seksjonen.
- om uavhengig togveglegging er mulig; hvis ikke, må den enkeltsporede seksjonen regnes som en blokkstrekning lengre enn den egentlig er.
- hastighet over sporveksel i avvik.
Hvis vi tar utgangspunkt i en gitt kapasitetsutnyttelse på den i utgangspunktet dobbeltsporede strekning, spiller også graden av ensartethet (hvor blandet eller ensartet trafikken er) inn. For en strekning med ensartet trafikk eller utstrakt puljekjøring blir det flere tog som skal passere flaskehalsen enn for en strekning med i utgangspunktet maksimalt blandet trafikk. Dette skyldes at den enkeltsporede delstrekningen normalt er så kort at ulikhet i togslag gir vesentlig mindre ulikhet i kjøretid over denne delstrekningen enn over totalstrekningen. Jo flere tog pr. tidsenhet som skal trafikkere den enkeltsporede delen, desto høyere kapasitetsutnyttelse og desto mer spredning av forsinkelsene.
Når man skal vurdere en streknings kapasitet i forbindelse med nyanlegg eller utbygginger, kan det være aktuelt å ta med kapasitet i feilsituasjoner og ved vedlikehold slik som nevnt ovenfor. Hvis trafikken skal avvikles greitt også i slike feilsituasjoner, kreves overkapasitet ved normal drift, dvs. lavere kapasitetsutnyttelse.
For enkeltspor vil mange feilsituasjoner selvsagt føre til full stopp i trafikken, så slike betraktninger er da mindre aktuelle enn for dobbeltspor.
Teori for forsinkelsesforplantning
Vi ser her på konsekvensene av enkeltfeil. Det forutsettes da en initiell forsinkelse for bare ett tog, og man beregner hvordan denne forplanter seg til andre tog (sekundære forsinkelser, følgeforsinkelser). Det antas videre at det ikke oppstår nye primærforsinkelser før virkningene av den forrige har dødd ut.
Disse feiltypene omfatter det vi i forrige avsnitt kalte kortvarige feil på materiell eller infrastruktur. Videre vil også varige feil på materiell som ikke hindrer toget i å kjøre, kunne dekkes her - i hvert fall for dobbeltspor. Den initielle forsinkelsen må da settes til den forsinkelse dette toget har ved strekningens slutt. En initiell forsinkelse kan også oppstå av andre grunner enn rent tekniske, f.eks. ved forlenget oppholdstid pga. stor trafikk.
Det er også en forutsetning at alt fungerer normalt etter at den første forsinkelsen har oppstått; både tekniske forhold, samt kjøretider, oppholdstider o.l.
Vi behandler først situasjonen med en primærforsinkelse som oppstår ute på en strekning hvor det ikke regnes med noen mulighet til forbikjøring. Deretter ser vi på konsekvensene av forsinkelser på eller før den første stasjonen på strekningen vi betrakter.
Dobbeltspor med ensartet trafikk
Teorien som presenteres her, er i hovedsak hentet fra ref. / 5 /. Vi ser da på en strekning med ensartet trafikk hvor togene trafikkerer med en rutemessig togfølgetid tr (konstant eller midlere). Denne må være større enn den teknisk minste togfølgetid for strekningen, tt. Differansen mellom disse kalles buffertiden, tb:
og uttrykker den buffer man har mot at forsinkelse fra et tog skal spre seg til neste tog.
Forsinkelser betegnes p og indekseres med tognummer hvor det toget som initielt blir forsinket, har nr. 1. Vanligvis er den initielle forsinkelse p1 større enn buffertiden tb slik at forsinkelsen spres til neste tog. Togene kjører da med den teknisk minste togfølgetid tt slik at hvert tog får en forsinkelse som er tb mindre enn det forrige:
Slik reduseres forsinkelsen fra tog til tog inntil den blir null. Vi kaller antall tog som berøres av sekundære forsinkelser for j, og det siste toget som blir påvirket av den initielle forsinkelse p1 har da forsinkelsen
hvor ε er et tall mellom 0 og 1.
Et eksempel med j = 3 er vist i følgende figur.
Figur 22: Forsinkelsesforplantning ved ensartet trafikk (j=3).
Summen av alle forsinkelser, som man får pga. av den initielle forsinkelsen p1, er da summen av disse (j+1) forsinkelsene:
Vi har her brukt uttrykket for summen av en aritmetisk rekke. Uttrykket ovenfor omformes videre ved å sette inn pj+1 = εtb og j = (p1/tb) - ε:
Dette kan omformes til
Siden ε ligger i intervallet mellom 0 og 1 har vi alltid
Siden vi bare ser på situasjoner hvor p1>tb, kan vi derfor med god tilnærmelse sette
Dette er et mye enklere uttrykk å behandle selv om det er en svak underestimering av den samlede forsinkelse som p1 fører til. Tilnærmelsen, som her er gjort, er ekvivalent med å sette pj+1 = 0; dvs. forsinkelsen på det siste toget som blir berørt, neglisjeres.
I uttrykket ovenfor er (p1/tb +1) det samme som antall forsinkede tog (= j+1), mens p1/2 er den gjennomsnittlige forsinkelse for alle de forsinkede togene. Uttrykket for den samlede forsinkelse får da den enkle tolkning:
sum forsinkelse = antall forsinkede tog * gjennomsnittlig forsinkelse.
Siste del av uttrykket ovenfor kalles forplantningsfaktoren for forstyrrelser (y):
Dette uttrykket er utledet under forutsetningen at det blir følgeforsinkelser, dvs. at p1>tb. For mindre verdier av p1 har vi derfor y(p1) = 1.
Med denne forplantningsfaktoren kan uttrykket for den summerte forsinkelse tilnærmet uttrykkes som
Eksempel: En av de få norske strekninger med tett ensartet trafikk er fellesstrekningen for T-banene i Oslo. Vi skal her beregne forsinkelsesforplantningen på denne strekningen i og utenfor rushtid. Vi skal regne med initialforsinkelser som oppstår inne på fellesstrekningen, av størrelse 2 og 5 min, dvs. p1 = 120, h.h.v. 300s.
Den teknisk minste togfølgetid for denne strekningen settes vanligvis til 90s.
Utenom rushtid kjøres 4 tog pr. kvarter, dvs. (gjennomsnittlig) rutemessig togfølgetid er 225s. Buffertiden blir
Med en initialforsinkelse på 2 min er p1 < tb og y(p1) = 1, dvs. det blir ingen forplantning av forsinkelser.
Med en initialforsinkelse på 5 min blir forplantningsfaktoren
Totalforsinkelsen blir da 8 min, dvs. følgeforsinkelsen er 3 min.
I rushtiden har det blitt kjørt et varierende antall tog gjennom tidene. Vi vil her se på en situasjon med ett innsatstog fra hver bane, dvs. 8 tog pr. kvarter. Dette gir en rutemessig togfølgetid på 112s, og buffertiden blir da
Dette gir en vesentlig kraftigere forplantning av forsinkelser. Med en initialforsinkelse på 2 min blir forplantningsfaktoren
Totalforsinkelsen blir dermed ca. 6.5 min, dvs. at følgeforsinkelsen er 4.5 min, mens det utenom rushtiden ikke ble noen følgeforsinkelse i det hele tatt med en slik initialforsinkelse.
Med en initialforsinkelse på 5 min blir forplantningsfaktoren
Totalforsinkelsen blir dermed ca. 36.5 min, dvs. at følgeforsinkelsene samlet er 31.5 min, mens det utenom rushtiden ble en samlet følgeforsinkelse på 4.5 min. med en slik initialforsinkelse. Følgeforsinkelsene (forårsaket av en initialforsinkelse på 5 min.) blir altså 7 ganger så store når togantallet dobles.
Vi har ovenfor regnet med den samme teknisk minste togfølgetid på 90s både i og utenfor rushtid. Denne togfølgetiden forutsetter en oppholdstid på 20s. Oppholdstiden vil selvsagt variere noe fra tog til tog og fra stasjon til stasjon, men den vil gjennomgående være lengre i rushtiden, og den vil oftest øke ytterligere ved forsinkelser. Vi vil her se på konsekvensene av en økning av oppholdstiden til 30s på den dimensjonerende stasjon på strekningen. Dette er ingen urealistisk verdi ved stor av- og på-stigning. Den teknisk minste togfølgetiden blir da 100s og buffertiden bare 12s. Med en initialforsinkelse på 5 min blir forplantningsfaktoren
Dette betyr altså at den initielle forsinkelse fører til en total forsinkelse som er 13 ganger så stor. Totalforsinkelsen blir dermed ca. 65 min, dvs. at følgeforsinkelsene samlet er 60 min. En økning av den teknisk minste togfølgetiden fra 90 til 100s fører altså til nesten en dobling av følgeforsinkelsene i dette tilfellet. Årsaken er selvfølgelig at man har en svært høy kapasitetsutnyttelse med en tilsvarende liten buffertid.
I det siste tilfellet er antall tog som berøres av følgeforsinkelser
Med 8 tog pr. kvarter vil det si at alle tog blir forsinket i de neste 47 minuttene. I praksis vil dette som oftest bety resten av rushtiden.
Dobbeltspor med blandet trafikk
I ref. / 5 / behandles kun situasjonen hvor mange langsomme tog (godstog) regelmessig kjøres forbi av noen få raske tog (ekspresstog). Denne situasjonen er helt uaktuell for nåværende norske dobbeltsporede strekninger og sannsynligvis også lite relevant for planlagte strekninger.
Derfor vil vi her modifisere uttrykket for ensartet trafikk til å dekke situasjonen på norske dobbeltspor.
Vi ser da på en situasjon hvor det vekselvis kjøres n raske (direkte) og m langsomme (stoppende) tog. Figur 15 viser et eksempel på en slik situasjon. Togene som inngår i en pulje med langsomme tog og den etterfølgende pulje med raske tog vil vi her kalle en gruppe. Som før betegner Δt differansen i kjøretid mellom et raskt og et langsomt tog over den strekningen vi ser på.
Den teknisk minste togfølgetid vil vanligvis være litt forskjellig for ulike togtyper (se kap. 3.6.3), men her setter vi togfølgetidene for tog i samme gruppe og for et langsomt etter et raskt til tt. Tilsvarende har vi en (midlere) rutemessig togfølgetid på tr for alle disse tilfellene. Togfølgetidene for et raskt tog etter et langsomt er tt + Δt teknisk sett og tr + Δt rutemessig. Disse togfølgetidene refererer utgangsstasjonen. Sett fra forskjellige steder på strekningen vil buffertiden mellom et tog fra hver pulje variere med hvor på strekningen man er.
En forsinkelse på et tog i en gruppe vil føre til forsinkelse på de etterfølgende tog i samme gruppe på samme måte som for ensartet trafikk. Hvis i og (i+1) betegner to tog i samme gruppe, gjelder altså fortsatt
Men hvis i betegner siste tog i en gruppe (og i+1 altså første tog i neste gruppe), har vi isteden
, for
, for
Forsinkelsesforplantningen forgår altså som for ensartet trafikk, unntagen mellom siste tog i puljen av raske tog og første tog i puljen av langsomme tog. Mellom disse to togene øker buffertiden fra tb ved utgangsstasjonen til (tb + Δt) ved sluttstasjonen. Her er det altså p.g.a. den blandede trafikk (og dermed lavere togantall) en større buffer mot spredning av forsinkelser. En forsinkelse p1 < tb vil derfor ikke spre seg til neste pulje av langsomme tog uansett hvor liten buffertiden er. Det forutsettes da at Δt er vesentlig større enn tb slik det vanligvis er i praksis.
I neste figur vises et eksempel på en forsinkelse for første tog i en gruppe (to langsomme og ett raskt tog) som sprer seg til hele denne og neste gruppe.
Figur 23: Eksempel på forsinkelsesforplantning ved blandet trafikk (n=2, m=1, j=5).
Ved blandet trafikk er det vesentlig mer komplisert å regne ut Σpi enn tilfellet var for ensartet trafikk. Summen vil også avhenge av hvilket nummer i gruppen toget med den første og den siste forsinkelsen har. For å bli kvitt denne avhengigheten antar vi derfor at forsinkelse kan oppstå på et hvilket som helst tog i gruppen med samme sannsynlighet. Tilsvarende antas at det nummer i gruppen som får den siste følgeforsinkelsen også er jevnt fordelt. Da kan man midle over alle forekomstene og således komme videre. Under disse forutsetningen kan man etter en del regning vise at den midlere samlede forsinkelse også nå kan uttrykkes ved
Som ved ensartet trafikk, gjør vi også her tilnærmelsen pj+1 = 0.
Formelt er dette det samme uttrykk som vi fant ved ensartet trafikk. Imidlertid er det nå en annen sammenheng mellom j og p1 enn ved ensartet trafikk (hvor vi med tilnærmelsen pj+1 = 0 hadde j = p1/tb).
For å finne en enkel sammenheng mellom j og p1 i denne situasjonen må vi forutsette at følgeforsinkelsen berører et helt antall grupper av tog (dvs. at j/(n+m) er et heltall). For forplantningen av forsinkelser fra et tog til neste er det da ett tilfelle med buffertid (tr + Δt - tt) for hver gruppe, mens de øvrige har buffertid (tr - tt). Vi kan da beregne en midlere buffertid () for blandet trafikk:
Sammenhengen mellom antall forsinkede tog og initialforsinkelsen kan da uttrykkes
Dermed kan den midlere samlede forsinkelse under disse forutsetninger uttrykkes
Også dette uttrykket for den samlede forsinkelse kan gis tolkningen:
sum forsinkelse = antall forsinkede tog * gjennomsnittlig forsinkelse.
Selv om dette uttrykket formelt er svært likt uttrykket for ensartet trafikk, kan det ikke uten videre brukes på samme måte. Pga. de forutsetninger som er gjort under utledningen, kan ikke dette uttrykket benyttes til å regne ut summen av alle forsinkelser i en konkret situasjon, gitt initialforsinkelse og det nummer i gruppen den gjelder. Avviket er særlig merkbart når p1/ er liten. Men slike behov kan enkelt dekkes ved å ta utgangspunkt i den gitte tallverdi for p1 og den aktuelle ruteplan.
Uttrykket ovenfor er imidlertid beregnet til bruk ved sammenlikning av ulike situasjoner m.h.p. infrastruktur og ruteplan, hvor initialforsinkelse og nummer i gruppen ikke er spesifisert. For slike gjennomsnittsbetraktninger har de tilnærmelser som er gjort, liten betydning.
Vi ser bl.a. at siden den midlere buffertid ved blandet trafikk, tb, er større enn tb ved ensartet trafikk, blir forplantningen mindre ved samme utnyttelsesgrad av kapasiteten. Samme utnyttelsesgrad tilsvarer imidlertid et vesentlig lavere togantall ved blandet trafikk enn ved ensartet trafikk, og dette er også årsaken til at forsinkelsene forplanter seg mindre. For situasjonen med forsinkelse fra utgangsstasjonen blir forholdet annerledes, se kap. 5.2.4.
Eksempel: Vi vil her se på et par situasjoner med blanding av stoppende og direkte tog som har rimelig relevans for JBVs forstadsstrekninger (Oslo - Lillestrøm/Ski/Asker).
Først ser vi på de samme forhold som i eksempelet i kap. 2.2.2 med stoppende og direkte tog annenhver gang. Vi setter fortsatt teknisk minste togfølgetid tt til 2 min og differansen i kjøretid Δt til 10 min.
Et typisk rutemønster med et tog av hver type pr. kvarter gir altså 8 tog/time, mens den teoretiske maksimalkapasitet er 9 tog/time (beregnet i eksempelet i kap. 2.2.2). Den rutemessige togfølgetid (tr) finnes (jfr. Figur 23) fra likningen
Dette gir tr = 2.5 min., og den midlere buffertiden blir da
Vi ser på en initialforsinkelse (som oppstår ute på strekningen) på 15 min. (Uttrykket utledet i det foregående forutsetter at forsinkelsen sprer seg til et helt antall grupper). Forplantningsfaktoren blir da
Den totale forsinkelsen (p1y) blir altså 30 min., dvs. følgeforsinkelsen er 15 min. Selv med en så høy kapasitetsutnyttelse som 89% (= 8/9), blir altså forsinkelsesforplantningen svært moderat sammenliknet med ensartet trafikk. Årsaken til dette er primært det lave antall tog pr. time.
Vi skal så se på en ruteplan med noe flere tog. Det er fortsatt stoppende tog hvert kvarter, men vi ser nå på 2 direkte tog pr. kvarter, altså totalt 12 tog/time. For sammenlikningens skyld vil vi ha nøyaktig samme kapasitetsutnyttelse som ovenfor, og differansen i kjøretid (Δt) må da være 7.33 min.
Den rutemessige togfølgetid (tr) finnes på samme måte som ovenfor, og den blir også nå 2.5 min. Den midlere buffertiden blir nå
Vi lar fortsatt initialforsinkelsen være 15 min. Forplantningsfaktoren blir da
Følgeforsinkelsen (p1y - p1) blir nå 30 min., altså en dobling i forhold til den første ruteplanen, selv om kapasitetsutnyttelsen er den samme i begge situasjonene.
Vi ser av dette eksempelet at forsinkelsesforplantningen ved blandet trafikk er ganske forskjellig fra situasjonen med ensartet trafikk selv om formeluttrykkene er nesten like. Forsinkelsesforplantningen ved blandet trafikk øker med økende antall tog selv om kapasitetsutnyttelsen er uendret. Dette til forskjell fra ensartet trafikk hvor kapasitetsutnyttelsen var den sentrale faktor. Dette omhandles noe mer i kap. 5.3.
Enkeltspor
På samme måte som for kapasitetsberegninger, er også beregning av forsinkelsesforplanting vesentlig mer komplisert for enkeltspor enn for dobbeltspor (ensrettet trafikk).
Også for enkeltspor kan man komme fram til uttrykk av formen
Uttrykket for y er imidlertid mer komplisert enn for dobbeltspor og inneholder flere parametere. Likeledes må man gjøre flere forutsetninger for å “komme fram” slik at avstanden fra virkelige ruteplaner blir større.
Ved trafikk i begge retninger på samme spor vil en forsinkelse også forsinke tog i motgående retning slik at y normalt er større da enn ved trafikk i en retning.
Vi skal her gi en kort omtale av utledningen gjort i ref. / 5 / for enkeltspor.
For en strekning som består av bare ett strekningsavsnitt, blir resultatet det samme som ved trafikk i en retning.
Mer generelt ser vi på en strekning som består av a like strekningsavsnitt. Vi ser bare på ruteplaner bestående av et enkelt nett (ingen puljekjøring) av like tog med kryssing på alle stasjoner. Det er videre forutsatt at tidstapet ved kryssing alltid legges til togene i en og samme retning. Det er da implisitt forutsatt at alle togene i denne retningen har lavere prioritet enn togene i motsatt retning. Vi regner også her med en konstant buffertid tb mellom alle togpar. Denne buffertiden er også lagt til togene i den lavest prioriterte retningen.
Uansett hvor på strekningen den første forsinkelse p1 oppstår, regner vi, som tidligere, med at toget over resten av strekningen beholder denne forsinkelsen (implisitt er det da forutsatt at dette toget kjører i den prioriterte retningen). Over det siste strekningsavsnittet (for dette toget) vil j etterfølgende tog forsinkes (sum begge retninger). Som for dobbeltspor er j = (p1/tb) når vi gjør tilnærmelsen pj+1= 0. Summen av disse forsinkelsene er da som tidligere utledet p1(p1/tb + 1)/2.
I tillegg kommer forsinkelser på en del tog i motgående retning tidligere på strekningen. Dette dreier seg om et tog pr. strekningsavsnitt f.o.m. det avsnitt der primærforsinkelsen oppsto t.o.m. det nest siste avsnittet på strekningen. Dette utgjør fra (a-1) til 0 tog avhengig av om primærforsinkelsen oppsto i alt fra første til siste strekningsavsnitt (i dette togets kjøreretning). I gjennomsnitt (over alle a) blir dette (a-1)/2 tog. Disse får alle en forsinkelse av størrelse (p1 - tb).
Summen av forsinkelser blir da i gjennomsnitt
Hvis vi ønsker å uttrykke dette med en forplantningsfaktor y, får vi som tidligere
hvor y nå er gitt ved
Dette uttrykket er som de tidligere, utledet under forutsetningen p1>tb. Da ser vi at forplantningen i følge dette uttrykket er større enn for dobbeltspor (ensrettet trafikk) og at forplantningen øker med økende antall strekningsavsnitt.
I denne utledningen er det ikke tatt hensyn til at togene i den lavt prioriterte retningen (de som tar tidstapet ved kryssingene) vil få redusert forsinkelsen før de når slutten av strekningen. Dette skyldes buffertiden mellom hvert tog, som tenkes lagt til kjøretiden for disse togene ved forlenget oppholdstid på hver stasjon. Uttrykket utledet ovenfor gjelder altså summen av de maksimale forsinkelser underveis, ikke forsinkelser til endestasjonene. Hvis man isteden ser på summen av forsinkelsene ved ankomst til endestasjonene, blir ikke summen av forsinkelsene uten videre større for enkeltspor enn for dobbeltspor.
Forsinkelse ved strekningens start
Vi vil her se på konsekvensene av forsinkelser som oppstår på eller før den første stasjonen på strekningen vi betrakter. Den øvrige trafikk kan da gå uhindret inntil det forsinkede toget er klar til å kjøre.
For ensartet trafikk (dobbeltspor) må vi se på to litt forskjellige tilfeller.
I det første tilfellet er strekningen “ledig” når det initielt forsinkede tog er klar til å kjøre, slik at dette ikke får noen tilleggsforsinkelse. Uansett når dette toget starter, vil neste tog kunne følge etter på teknisk minste togfølgetid, tt. Den maksimale følgeforsinkelsen for ett tog blir altså bare tt uansett initialforsinkelse. For den følgende utledning forutsettes også at den teknisk minste togfølgetid, tt, er større enn buffertiden tb.
Den samlede forsinkelse p.g.a. initialforsinkelsen p1 blir da
Vi har her brukt ≤ fordi det siste leddet vil variere (den første følgeforsinkelsen vil ligge et sted i intervallet [max (tt-tb, 0), tt]).
I det andre tilfellet er strekningen ikke “ledig” når det initielt forsinkede toget er klar til å kjøre slik at dette får en tilleggsforsinkelse som vil variere mellom 0 og tt. Den første følgeforsinkelsen blir da (tt-tb).
Den samlede forsinkelse p.g.a. initialforsinkelsen p1 blir
Vi får altså samme uttrykk for den samlede forsinkelse i begge tilfellene.
Dette uttrykket kan ikke omformes til p1 multiplisert med en forsinkelsesforplantning y fordi siste del er uavhengig av p1. Men vi kan sette
I denne situasjonen er altså følgeforsinkelsene uavhengig av p1, og de er av et lite omfang unntatt for ekstrem kapasitetsutnyttelse (tb nær null).
Denne utledningen er gjort under forutsetningen tt > tb. For den motsatte situasjonen har vi ganske enkelt
Dette svarer til at vi setter y(tt) = 1 når tt < tb slik som vi tidligere har gjort (når p1 < tb).
Eksempel: Vi vil her igjen se på fellesstrekningen for T-banene i Oslo, slik som i eksempelet i kap. 5.2.1. Men vi ser nå på en situasjon hvor et tog kommer forsinket fram til innfasingspunktet til fellesstrekningen. Togene fra de andre banene kan da gå uhindret inntil det forsinkede toget ankommer slik at følgeforsinkelsene her er uavhengig av initialforsinkelsen. (Vi forutsetter da at initialforsinkelsen ikke er så stor at neste tog fra samme bane berøres).
Vi ser fortsatt på situasjonen utenfor og i rushtid, med rutemessig togfølgetid på henholdsvis 225 og 122s. Med en teknisk minste togfølgetid (tt) på 90s blir buffertiden (tb) fortsatt henholdsvis 135 og 22s.
Vi kaller de samlede følgeforsinkelser for pf, og denne er da gitt ved
I situasjonen utenfor rushtid er tt < tb slik at y(tt) = 1, og de samlede følgeforsinkelser er da maksimalt tt = 90s.
I rushtiden er de samlede følgeforsinkelser maksimalt
min
Konsekvensene er altså betydelig mindre enn når forsinkelsen oppstår inne på fellesstrekningen. Vi understreker at dette resultatet forutsetter at øvrige tog går uhindret inntil det forsinkede toget er klart til å kjøre.
Vi går så over til å se på blandet trafikk. Også der er det to ulike tilfeller å diskutere.
Hvis det initielt forsinkede toget venter til det kan kjøre sammen med neste pulje av sine “egne” tog, blir også her den maksimale følgeforsinkelsen tt. Men tilleggsforsinkelsen for det initielt forsinkede toget kan da bli stor. I prinsippet kan den bli opptil Δt + ntr, men i slike situasjoner vil man i praksis ikke la toget vente til neste pulje. Da det dominerende leddet normalt er Δt, vil vi si at tilleggsforsinkelsen det første toget får, normalt er begrenset av Δt. Den samlede forsinkelse blir da
For følgeforsinkelsene har vi her brukt uttrykket for ensartet trafikk fordi forsinkelser av størrelse tt sjelden vil spre seg til neste gruppe.
Hvis det initielt forsinkede toget skal starte (og kjøre uhindret) med det samme det er klar til å kjøre (dvs. få minst mulig tilleggsforsinkelse), vil følgeforsinkelsene ofte bli større enn ovenfor. Generelt kan man da sette
hvor p’ angir differansen mellom start-tiden for det forsinkede toget og det siste rutemessige toget. Om man skal bruke den midlere buffertid () eller bare tb, vil avhenge av størrelsen på p’. p’ kan i prinsippet variere fra tt til (Δt + mtr). I praksis vil vi nok kunne regne med p’≤ Δt slik at vi får
Vi ser altså at konsekvensene av en initialforsinkelse ved strekningens start kan bli vesentlig større ved blandet trafikk enn ved ensartet trafikk. Dette skyldes at det gir større konsekvenser å bytte om rekkefølgen av tog med ulike kjøretider enn å bytte om rekkefølgen mellom ensartede tog.
Som en rimelig midlere verdi for p’ kan vi bruke 0.5Δt. Med typiske verdier for Δt, tt og tb vil det da være mest rimelig å bruke den midlere buffertid () slik at vi i gjennomsnitt grovt sett kan sette
Eksempel: Vi vil her igjen se på forholdene på JBVs forstadsstrekninger.
Vi skal anslå de samlede følgeforsinkelser (pf = Σpi - p1) for det første ruteopplegget vi brukte i eksempelet i kap. 5.2.2. Vi ser altså på situasjonen med stoppende og direkte tog annenhver gang hvor differansen i kjøretid (Δt) er 10 min. Den midlere buffertid () er fortsatt 5.5 min. De samlede følgeforsinkelser blir da normalt begrenset av
[min]
Mens vi for et grovt gjennomsnittlig anslag får
[min]
Vi ser at følgeforsinkelsen blir noe mindre når forsinkelsen oppstår ved strekningens start enn ute på strekningen (eksempelet i kap. 5.2.2). Men det er ikke den dramatiske nedgangen som vi fikk i eksempelet med ensartet trafikk.
I tillegg til de anslag over forsinkelser som er gjort ovenfor, kommer det forhold at blandet trafikk medfører betydelig vanskeligere avgjørelser for togleder. Når en forsinkelse oppstår ved strekningens start, vet man ofte ikke hvor lang tid det vil ta før det initielt forsinkede toget er klart. Beslutningen om togrekkefølge må normalt tas før man vet dette, og en optimal beslutning avhenger derfor av et korrekt estimat over hvor stor den initielle forsinkelse vil bli. Derfor vil følgeforsinkelsene i praksis lett bli betydelig større enn verdiene man får ved slike beregninger. Ved ensartet trafikk er toglederens arbeid lettere i dette henseende, og beregningene gjort i det tilfellet er derfor mer realistiske.
For den skjematiske situasjonen på enkeltspor som vi har behandlet tidligere i dette kapitlet, vil vi kunne gjøre liknende betraktninger. Vi kan da sette
hvor p’ angir differansen mellom start-tiden for det forsinkede toget og det siste rutemessige toget. p’ kan altså variere fra tt til tr. Videre vil alle motgående tog berøres, slik at vi har erstattet (a - 1)/2 med a i det siste leddet (dette kom fra midling over alle strekningsavsnitt hvor den initielle forsinkelse kunne oppstå, se kap. 5.2.3).
Selv om konsekvensene også her er uavhengige av p1, blir de likevel betydelige.
Sammenheng mellom forsinkelser og kapasitetsutnyttelse
Basert på de foregående avsnitt skal vi her vise relasjoner mellom forsinkelse og kapasitetsutnyttelse for noen enkle rutemodeller / situasjoner.
Noen forsinkelse-variable og relasjon til begrepet punktlighet
I det foregående har vi uttrykt summen av forsinkelser som en initialforsinkelse p1 fører til, ved
hvor uttrykket for forplantningsfaktoren y avhenger av type strekning og ruteopplegg.
Vi ser så generelt på en strekning av lengde L hvor det over et visst tidsrom, f.eks. et døgn, trafikkerer N tog. Hyppigheten av initialforsinkelser kan uttrykkes på forskjellige måter. Det enkleste er, som i ref. / 5 /, å forutsette ett tilfelle pr. q togkm i gjennomsnitt. I det gitte tidsrommet vil det da oppstå NL/q initielle forsinkelser. Det forutsettes at det er så lenge mellom hver initiell forsinkelse at alle følgeforsinkelsene er forsvunnet før en ny initialforsinkelse oppstår. Den totale forsinkelse P i det gitte tidsrom blir da
Dette uttrykket tar imidlertid ikke hensyn til at størrelsen på initialforsinkelsen p1 vil variere fra gang til gang. For å ta hensyn til dette må man kjenne sannsynlighetsfordelingen for initielle forsinkelser, her kalt f(p1). Forventningen av den totale forsinkelse over et langt tidsrom (omfattende N tog) vil da kunne uttrykkes
I praksis vil det være vanskelig å finne pålitelig verdi av en slik sannsynlighetsfordeling. Det er også sjelden spørsmål etter den totale forsinkelse i den her brukte betydning.
Når begrepet punktlighet benyttes, er det ofte i form av prosentvis andel av tog med forsinkelse over en viss størrelse. Et slikt begrep er matematisk vanskelig å håndtere. Innen den formalisme som her er presentert, vil man antagelig komme nærmere ved å se på gjennomsnittlig forsinkelse pr. tog: P/N. Siden vi alltid tar utgangspunkt i en spesifikk initialforsinkelse p1, vil vi se på gjennomsnittlig forsinkelse pr. tog og initialforsinkelse:
Da vi her ikke tar opp hyppigheten av primære forsinkelser (q), må L/q betraktes som en konstant i denne sammenheng. Vi sitter da tilbake med forplantningsfaktoren y(p1) som den sentrale størrelse å drøfte. Beklageligvis er også denne avhengig av p1, men denne avhengigheten kan man ikke komme bort fra. For sammenlikning av ulike alternativer m.h.p. infrastruktur, utnyttelsesgrad osv. kommer man oftest langt ved å sammenlikne ved samme primærforsinkelse. Dette vil derfor bli gjort i det følgende.
Dobbeltspor med ensartet trafikk
Vi går så videre med den samme type situasjon som ble behandlet i kap. 5.2. Der ble forsinkelsesforplantningen y uttrykt som funksjon av initialforsinkelsen p1 og med buffertiden tb som parameter. Da buffertiden er en størrelse som mange ikke “har noe forhold til”, skal vi trekke inn kapasitetsutnyttelsen som parameter isteden for buffertiden. Vi vil da bruke utnyttelsesgraden u fra kap. 2.3, definert som forholdet mellom den praktiske og den teoretiske kapasitet, eller som forholdet mellom det virkelige togantall pr. tidsenhet og det teoretisk maksimale.
Forholdet mellom det faktiske togantall (N) i et tidsrom T og den faktiske buffertid (tb) uttrykkes på samme måte som den praktiske kapasitet
Det maksimale togantall i et tidsrom T er lik den teoretisk maksimale kapasitet
Utnyttelsesgraden er da
Ved å innføre tr herfra får vi at buffertiden kan uttrykkes
Dette kan brukes til å eliminere buffertiden i forplantningsfaktoren y slik at denne isteden uttrykker avhengigheten av utnyttelsesgraden u:
Når vi skal se på hvordan forplantningen av forsinkelser varierer med utnyttelsesgraden, kan vi betrakte p1/2tt som en parameter (her kalt k) slik at vi kan sette
For konkret å vise hvordan forsinkelsesforplantningen “eksploderer” med økende kapasitetsutnyttelse har vi satt opp en tabell som viser y for noen u-verdier.
| Utnyttelsesgrad | Forsinkelsesforplantning (y) |
| 25% (u = 1/4) | 0.33k + 0.5 |
| 33% (u = 1/3) | 0.5 k + 0.5 |
| 40% (u = 2/5) | 0.67k + 0.5 |
| 50% (u = 1/2) | 1 k + 0.5 |
| 66% (u = 2/3) | 2 k + 0.5 |
| 75% (u = 3/4) | 3 k + 0.5 |
| 80% (u = 4/5) | 4 k + 0.5 |
| 90% (u = 9/10) | 9 k + 0.5 |
| 95% (u = 19/20) | 19k + 0.5 |
Her ser man f.eks. at en økning av kapasitetsutnyttelsen fra 50 til 75% fører til at forsinkelsesforplantningen nesten tredobles. Uansett initialforsinkelse blir altså konsekvensene omtrent tre ganger så store bare som følge av denne økte utnyttelse. Tilsvarende fører en videre økning av utnyttelsesgraden til 90% til ytterligere nesten en tredobling.
Eksempel: Vi vil her se på beregningene i eksempelet i kap. 5.2.1 (fellesstrekningen for T-banene i Oslo) i lys av utledningen i det foregående og tabellen ovenfor.
Den teknisk minste togfølgetiden satte vi til 90s (1.5min.). Den teoretiske kapasiteten er altså 10 tog/kvarter. Vi beregnet forsinkelsesforplantningen for 4 og 8 tog/kvarter; kapasitetsutnyttelsen var altså 40% utenom rushtid og 80% i rushtid.
Av tabellen ovenfor kan vi raskt sette opp forholdet mellom forplantningsfaktorene (her kalt y4 og y8) i de to situasjonene:
Dette forholdet avhenger, som vi ser, av k (= p1/2tt). For store verdier av k (dvs. for initialforsinkelser mye større enn den teknisk minste togfølgetid) er leddet 0.5 neglisjerbart i forhold til k slik at dette forholdet da blir
(for )
Dette betyr at forsinkelsesforplantningen ved store initialforsinkelser blir 6 ganger så stor i rushtiden (8 tog/kvarter) som utenom rushtiden (4 tog/kvarter).
I beregningene i eksempelet i kap. 5.2.1 benyttet vi en initialforsinkelse på 5 min., dvs, at parameteren k da var
Vi får da at y8/y4 ≈ 4.5. For en initialforsinkelse på 5 min. blir altså forsinkelsesforplantningen 4.5 ganger så stor i rushtid som utenfor rushtid. Dette samsvarer med verdiene beregnet i kap. 5.2.1.
I det følgende vises en grafisk framstilling av forplantningsfaktoren (y) som funksjon av utnyttelsesgraden (u). Nederste kurve viser forløpet for k = 1 (p1=2tt) og den øverste kurven for k = 3 (p1=6tt). På en strekning med teknisk minste togfølgetid (tt) på 2 min. svarer dette til initialforsinkelser på henholdsvis 4 og 12 min.
Figur 24: Forsinkelsesforplantning som funksjon av utnyttelsesgrad.
Vi ser at forsinkelsesforplantningen øker langsomt ved lav og moderat kapasitetsutnyttelse, men ved 60 - 80% utnyttelse (u = 0.6 - 0.8) blir stigningen merkbart raskere, og ved enda høyere utnyttelse blir det dramatisk økning i forsinkelsene selv ved meget liten økning i kapasitetsutnyttelsen.
I denne sammenheng vil vi også trekke inn forholdet mellom teoretisk og praktisk kapasitet. I kap. 1.2 ble den praktisk nyttbare kapasitet definert ved det antall tog som kan framføres med akseptabel punktlighet. Det ble da nevnt at denne definisjonen inneholder et element av skjønn i og med bruk av ordet “akseptabel”. Dette ser vi nå illustrert i den foregående figuren: Det er ikke noe enkelt punkt på kurven som tydelig markerer seg som det punkt hvor forsinkelsesforplantningen er uakseptabel ved høyere kapasitetsutnyttelse og akseptabel ved lavere.
I kap. 2.3 ble utnyttelsesgraden til bruk ved beregning av praktisk kapasitet satt til 60% for døgnkapasitet og 75% for timekapasitet. Vurdert ut fra denne figuren kan dette synes å være rimelige verdier siden de ligger i det området hvor kurvens stigning blir merkbart raskere.
Av figuren ser vi også at forplantningsfaktoren øker raskere når initialforsinkelsen er større (den øverste kurven har 3 ganger så høy initialforsinkelse som den nederste). Dette illustrerer det forhold at også typisk størrelse (og hyppighet) av initialforsinkelser har betydning for hvor mye av den teoretiske kapasitet som det er forsvarlig å utnytte.
Dobbeltspor med blandet trafikk
Vi ser så på blandet trafikk hvor vi tidligere har funnet at
hvor den midlere buffertid er gitt ved
Forholdet mellom det faktiske togantall (N) i et tidsrom T og de øvrige parametere er
hvor tr som før er den rutemessige togfølgetid mellom to like tog eller mellom et raskt tog og et etterfølgende langsomt.
Det maksimale togantall i et tidsrom T er lik den teoretisk maksimale kapasitet
hvor tt som tidligere er den teknisk minste togfølgetid mellom to like tog eller mellom et raskt tog og et etterfølgende langsomt.
Utnyttelsesgraden er da
Ved å innføre tr herfra får vi at den midlere buffertiden kan uttrykkes
Dette kan brukes til å eliminere den midlere buffertiden i forplantningsfaktoren y slik at denne isteden uttrykker avhengigheten av utnyttelsesgraden u:
For igjen å vise hvordan forplantningen av forsinkelser varierer med utnyttelsesgraden kan vi betrakte p1(n+m)/2Δt som en parameter (her kalt kb) slik at vi får
Vi ser her en stor forskjell fra ensartet trafikk idet forplantningsfaktoren holder seg begrenset selv ved 100% kapasitetsutnyttelse. Dette skyldes, som tidligere nevnt, at togantallet aldri kan bli så høyt ved blandet trafikk som ved ensartet trafikk.
Vi kan også si at forplantningsfaktoren alltid vil være begrenset av verdien ved maksimal kapasitetsutnyttelse (u=1) slik at vi for det vanlige tilfellet med maksimalt blandet trafikk (n=m=1) kan sette
Vi minner om at de uttrykkene for y som her er brukt, er basert på gjennomsnittsbetraktnigner og visse forutsetninger, bl.a. at forsinkelsene spres over et helt antall grupper (en pulje av hver togtype). For små forsinkelser som ikke oppstår på siste tog i gruppen, vil forplantningen være omtrent som for ensartet trafikk.
Samlende for all ensrettet trafikk (to eller flere spor) kan vi grovt sett si at forplantningen av forsinkelser styres av utnyttelsesgraden sett i forhold til ensartet trafikk u’ = N/Nmax der Nmax er maksimalt antall tog ved ensartet trafikk (Nmax = T/tt).
Enkeltspor
For enkeltspor er uttrykket for forsinkelsesforplantning utledet under mer skjematiske (mindre realistiske) forutsetninger, og det inneholder også parameteren antall strekningsavsnitt. Det er derfor vanskeligere å komme fram til en tilsvarende formulering basert på utnyttelsesgraden. Det virker rimelig at man for ensartet trafikk og et enkelt rutenett (som var den situasjonen uttrykket for y ble utledet for), vil få en liknende sammenheng mellom y og u som for ensartet trafikk på dobbeltspor, p.g.a. leddet (p1/ tb).
Bruk av simulering til kapasitetsstudier
Ordet simulere brukes vanligvis i betydningen “late som” eller “etterlikne”. En simuleringsmodell kan betraktes som en etterlikning av den virkeligheten man ønsker å simulere.
I alle praktiske situasjoner vil virkeligheten være for kompleks til at den kan simuleres eksakt i alle detaljer. Det vil alltid være nødvendig med en forenkling for å kunne representere virkeligheten innen rammen av det hjelpemiddelet (verktøyet) man har valgt. Dermed kommer man straks over i spørsmålet om gyldighet av modellen. Dette må alltid vurderes i forhold til de formål man vil bruke modellen til. Prinsipielt sett kan det ikke gjøres noen generell verifisering av en modell helt løsrevet fra formål.
Vanligvis blir simuleringen utført ved hjelp av en datamaskin. Da blir en teoretisk modell av en del av virkeligheten oversatt til et datamaskinprogram. Resultater fra dette programmet kan så jevnføres med målinger av virkeligheten.
Det kan være mange grunner til å lage en slik simuleringsmodell. Men ofte vil man på en eller annen måte eksperimentere med modellen for å lære noe om virkeligheten, fordi dette er enklere enn å eksperimentere med virkeligheten direkte.
I denne sammenheng vil vi omtale simuleringsmodeller anvendt til å undersøke kapasitet på jernbanestrekninger.
Problemstillinger egnet for simulering
Simulering representerer således en helt annen tilnærming til problemene enn de metodene vi har sett på i det foregående. Med simuleringsmodeller og datamaskiner kan man få representert infrastruktur, materiellegenskaper og ruteopplegg med den nøyaktighet man ønsker. Man kan da etterlikne de virkelige forhold i et jernbanesystem, og dette åpner muligheter for enkelt å gjennomføre eksperimenter med å endre systemets parametere, enten det gjelder infrastruktur, materiell eller ruter.
I motsetning til de enkle beregningsmetoder vi har sett på tidligere, kan ikke en simuleringsmodell uten videre gi noe direkte anslag for en streknings eller et nettverks kapasitet. Resultatene fra en simuleringsmodell er i utgangspunktet i form av avgangs- og ankomsttider for de enkelte tog fra/til stasjoner og eventuelle andre definerte steder. De forskjellige modeller kan ha ulike former for bearbeiding av disse basale data.
Hvis man ønsker å bruke en simuleringsmodell til å få et nøyaktig anslag over en streknings kapasitet i tog pr. tidsenhet, må man derfor bestemme seg for et kriterium for når kapasitetsgrensen er overskredet. Man må så prøve seg fram med ulike mengder tog inntil man finner et togantall som man bedømmer til å ligge på grensen.
Å svare på spørsmålsstillingen “hva er kapasitetsgrensen for systemet?” krever derfor et omfattende arbeid ved bruk av simuleringsmodeller. Oftest vil man være mer interessert i et svar i form av kvalitet på trafikkavviklingen når man kjører en gitt rutemodell på en gitt infrastruktur.
I det hele er direkte bruk av simuleringsteknikken best egnet for spørsmålsstillinger av formen “hva skjer hvis” (“what if”). Spørsmål etter grense, optimum o.l. krever en mer indirekte bruk med elementer av prøving og feiling.
Blant spørsmålsstillinger av typen “hva skjer hvis” kan man videre skille mellom relative og absolutte problemstillinger eller tilsvarende relativ og absolutt bruk av en simuleringsmodell. Med relativ bruk menes da å velge det beste blant flere spesifiserte alternativer, mens absolutt bruk sikter på å avgjøre om et gitt alternativ er godt nok eller ikke m.h.p. valgte kvalitetsparametere. Absolutt bruk vil ofte kreve en mer nøyaktig modell og en grundigere vurdering av modellens tilnærmelser og virkemåte enn relativ bruk.
Problemstillinger som er velegnet for simulering kan vi stort sett inndele i følgende hovedgrupper:
- finne det beste blant spesifiserte alternativer for infrastrukturen med et gitt ruteopplegg
- finne det beste blant spesifiserte alternative ruteopplegg med en gitt infrastruktur
- finne de viktigste flaskehalsene i et system
- avgjøre om en gitt ruteplan på en gitt infrastruktur vil gi tilfredsstillende trafikkavvikling.
De to første gruppene ovenfor er klare relative problemstillinger, og den siste en klar absolutt problemstilling. Nummer tre er litt annerledes og krever tilgang til spesielle typer resultater. Krav til nøyaktighet og virkemåte for denne problemstillingen er omtrent som for relative problemstillinger.
Gjennomføring av en simuleringsstudie er ofte et omfattende arbeid. Spesielt gjelder dette ved første gangs simulering av en strekning fordi data om infrastrukturen ofte utgjør hoveddelen av de opplysninger modellen trenger. Det er derfor viktig å ha klart formulerte spørsmålsstillinger før man starter. Likeledes må det være klart hvordan de resultater modellen gir, kan brukes til å besvare spørsmålene. Man bør også undersøke om enklere metoder, f.eks. noen av dem som er omtalt i det foregående, kan brukes. Problemstillinger velegnet for simulering bør være så komplekse at enkle metoder ikke gir fullgodt svar. Men også i slike situasjoner kan de enkle metoder omtalt tidligere utgjøre et nyttig supplement.
Om oppbygging av simuleringsmodeller
Vi vil her gå litt nærmere inn på oppbygging og virkemåte av simuleringsmodeller for jernbanesystemer. Framstillingen tar ikke sikte på å gi tilstrekkelig innsikt til selv å bygge modeller. Men også en bruker av en ferdig simuleringsmodell bør ha en viss kjennskap til modellens oppbygging og virkemåte. Dette er viktig både for å kunne vurdere om modellen gir en tilstrekkelig god beskrivelse av virkeligheten for den aktuelle problemstilling og for å kunne tolke de resultatene modellen gir.
Det er laget mange simuleringsmodeller for jernbanesystemer og flere er kommersielt tilgjengelige. Modellene har store ulikheter i oppbygging og til dels i virkemåte. Vi vil her ta opp en del generelle prinsipper ved konstruksjon av modeller og forhold som det er viktig å kjenne ved anskaffelse og bruk av en modell.
Transport-simulering egner seg godt for objekt-orientert programmering. Dette er en angrepsmåte som går ut på å bygge simuleringsmodellen opp av delmodeller som tilsvarer enheter i den virkelige verden. For en jernbanemodell vil noen typiske enheter være tog, sporfelt, sporveksel, signal, sikringsanlegg. For hver slik enhet samler man alle data om enheten og selve programkoden som beskriver dens “oppførsel”, i én programstruktur kalt “klasse”. De enkelte realiseringer av en klasse, som man får ved kjøring av programmet, kalles objekter. Som eksempel vil en slik modell bare ha én klasse tog, men et antall tog-objekter som tilsvarer antallet fysiske tog i den delen av virkeligheten som simuleres. Objektene påvirker hverandre ved å sende meldinger til hverandre og/eller ved å kalle klassens “metoder” (programfunksjoner).
Et annet viktig programmeringsteknisk skille går mellom tids-drevne og hendelses-drevne modeller (“time driven” / “event driven”). Begge disse kan benyttes enten modellen er objekt-orientert eller tradisjonelt oppbygd.
I en tids-drevet modell deles tiden opp i tidsskritt, normalt av samme lengde. For hvert tidsskritt beregnes hvor langt hvert tog flytter seg, hvilken hastighet det får ved tidsskrittets slutt, om noen signaler skifter, sporfelter belegges eller frigis osv. Alle objekter behandles i sekvens, og når et objekt trenger data fra andre objekter, benyttes tallverdiene fra forrige tidsskritt. Konsekvensene av endrede signal-bilder o.l. tas altså ikke hensyn til før i neste tidsskritt. Det blir dermed en økt reaksjonstid på i gjennomsnitt et halvt tidsskritt. Ved lange tidsskritt (f.eks. 30s) vil dette få merkbare konsekvenser for resultatene. For slike modeller er altså nøyaktigheten bedre jo kortere tidsskrittet er. På den annen side er regnetiden direkte proporsjonal med antall tidsskritt.
I en hendelses-drevet modell beregnes for hvert objekt hvor lang tid det går fram til neste hendelse. Med hendelse menes vanligvis noe som påvirker et annet objekt, f.eks. frigivelse eller belegg av sporfelt, endret signalbilde. Programsystemet sorterer objektene etter tidspunktet for neste hendelse for hvert objekt og utfører til enhver tid beregninger for det objektet som ligger først i denne køen.
Uansett hvordan en modell konkret er programmert vil den logisk sett kunne inndeles i visse hoveddeler. Vi vil omtale følgende hoveddeler (delmodeller):
- tog
- faste anlegg
- togledelse
- ruteplan
- strømforsyning (kontaktledning)
Disse delene påvirker hverandre; de viktigste sammenhengene er:
- Togledelse påvirker faste anlegg ved å legge togveger (inkl. å legge om sporveksler og stille signaler).
- Faste anlegg påvirker toget både ved baneparametere og signalbilder.
- Tog påvirker faste anlegg ved å belegge og frigi sporfelt.
- Ruteplan påvirker tog ved å bestemme destinasjon, stoppmønster og avgangstider.
- Tog og ruteplan påvirker togledelse til å gripe inn når det er avvik mellom rutetider og de aktuelle togenes tider.
- Tog påvirker strømforsyning ved at strømforbruk fører til redusert spenning, og strømforsyning påvirker tog ved at redusert spenning fører til redusert trekkraft.
Det er verdt å legge merke til at de påvirkningene som er beskrevet her, også finnes i det virkelige systemet. Dette er en av de viktige egenskapene ved en simuleringsmodell.
Så gis en kort omtale av hver av hoveddelene nevnt ovenfor.
Tog
Denne hoveddelen inneholder alle nødvendige data om hver togtype, samt program for beregning av kjøretid og hastighet.
Posisjon og hastighet er tilstandsvariable, dvs. de beskriver den situasjon toget er i ved ett bestemt tidspunkt. De øvrige togdata er faste parametere, som normalt er konstante for ett og samme tog.
Kjøretiden over en viss strekning og togets hastighet til enhver tid er bestemt av enkle fysiske bevegelseslover som tar hensyn til hastighet og akselerasjon/retardasjon.
De enkleste modelltyper benytter konstant akselerasjon og retardasjon for hver togtype og neglisjerer alle eller de fleste banedata som har betydning for akselerasjon/retardasjon. Man beregner da tilbakelagt strekning og oppnådd hastighet ved de velkjente likningene
Hastigheten begrenses av strekningens og togets maksimale hastighet.
Modeller som har en omfattende og detaljert beskrivelse av togenes bevegelse, bruker trekkraft- og bremsekurver, togets masse og lengde, samt baneparametere som stigning/fall og eventuelt også luftmotstand, rullemotstand, kurve- og tunnelmotstand. Bevegelseslikningen kan da uttrykkes
Her betegner
- Ft(t,v): trekkraft (hastighetavhengig) eller bremsekraft
- Fg(t) : kraftvirkning pga. banens fall eller stigning
- Ff(t,v): de samlede friksjonskrefter som modellen regner med
- m : toget totale masse
- a(t) : togets akselerasjon
Det kan også være aktuelt med data om maksimalt tillatt akselerasjon og retardasjon fordi visse togtyper har hastighetsautomatikk som ikke tillater mer enn en viss akselerasjon eller retardasjon selv om forholdene ellers skulle ligge til rette for det.
Enkelte modeller omfatter også strømforsyningsanlegget. Da vil trekkraften også være avhengig av kontaktledningens spenning i ethvert tidspunkt.
Utover disse forhold blir togets kjøring også bestemt av stoppesteder og oppholdstider gitt i ruteplanen og signaler som viser kjør eller stopp. For å beregne når et tog starter igjen etter et stopp tas det hensyn til nødvendig oppholdstid, rutemessig avgangstid og eventuelt signal som viser stopp.
Det som ovenfor er beskrevet, er rent tekniske forhold. Visse aspekter ved lokførerens kjøremåte bør også modelleres selv om ulike måter å gjøre dette på påvirker resultatet forholdsvis lite (sammenliknet med f.eks. modellering av togledelse). Normal kjøring modelleres ved at strekningens tillatte hastighet følges så langt togets trekkraft tillater det. Ulikheter i lokføreres reaksjonsmønster viser seg mest ved nedbremsing mot stopp. Strategien kan variere fra minimal kjøretid (maksimal bremsing) til en mer forsiktig kjøring hvor hastigheten reduseres tidlig etterfulgt av rulling eller svak bremsing før den siste bremsing mot stopp-punktet. De modelleringsmessige konsekvenser av dette er at man i simuleringsmodellen bør velge en lavere retardasjon enn den teknisk mulige.
Når et signal skifter fra stopp til kjør mens toget er under nedbremsing, starter toget å akselerere hvis det er innen siktavstand til signalet. Noen modeller har også siktpunkt på hvert signal med blant faste data, mens andre bruker en konstant avstand. Om strekningen som simuleres har automatisk togstopp (ATS), blir dette enklere fordi da tillates hastighetsøkning bare når toget har passert et signaloverføringspunkt (balise) eller når hastigheten har kommet ned til 40 km/h. Dermed blir det også noe mindre variasjon mellom ulike lokførere i slike situasjoner.
Når et signal skifter fra stopp til kjør, bør det alltid regnes med en viss reaksjonstid før lokfører reagerer, enten toget står stille eller er under nedbremsing.
For godstog har man i tillegg det forhold at bremsesystemet er utformet slik at det må regnes med en viss tid fra lokfører slår av bremsene til toget virkelig slutter å retardere (“løsetid for bremser”).
Faste anlegg
Faste anlegg består logisk sett av delsystemene sporplan, sikringsanlegg og signaler. Strømforsyning/kontaktledning behandles som en egen hoveddel hvis det i det hele tatt er med i modellen.
Store deler av faste anlegg er faste data som lengder, maksimalhastigheter, sammenheng mellom ulike sporseksjoner, mellom signal og sporfelt osv. Tilstandsvariable er typisk diskrete variable. F.eks. kan et sporfelt være belagt eller fritt; et signal kan vise et antall ulike bilder eller begrep; en sporveksel kan normalt ligge i en av to tilstander, osv. Noen modeller har også muligheten til at det kan være feiltilstander i tillegg til de normale tilstandene. “Likningene” for slike variable vil være boolske relasjoner. F.eks. vil betingelsene for innkjør på en enkel 2-spors stasjon uten samtidig innkjør kunne uttrykkes:
“innkjør til spor 1 tillatt” = “alle sporfelter fra innkjørsignalet til togveg slutt er frie” og “alle sporveksler i togvegen ligger riktig” og “ingen andre togveger er lagt (unntatt forlengelse av denne togvegen)”
Et virkelig sikringsanlegg har mange flere avhengigheter, men her er nevnt de som er mest aktuelle i en simuleringsmodell. For store stasjoner som skal simuleres i detalj, vil det bli svært mange slike avhengigheter, også i en simuleringsmodell.
Omfang og detaljeringsgrad av faste anlegg vil variere svært fra modell til modell. Dette vil man vanligvis få god informasjon om gjennom å se på hvilke data modellen har behov for. De mest detaljerte modeller har med hvert enkelt sporfelt, alle sporveksler, alle typer signaler osv. og hvordan disse forholder seg til hverandre. Enkle modeller nøyer seg med blokkstrekninger og hovedsignaler.
Detaljerte modeller har således et stort databehov, og det er et omfattende arbeid å fremskaffe og mate inn alle nødvendige data ved første gangs simulering av en strekning. Store deler av denne datamengden fins ofte i eksisterende databaser slik at arbeidsmengden og tidsforbruket kan reduseres hvis det finnes program for å overføre data fra eksterne kilder til simuleringsmodellen.
Eksempel
Vi skal her vise et eksempel på beskrivelse av faste anlegg til en enkel modell som ble utviklet ved NSB på slutten av 70-tallet. Eksempel og beskrivelse er hentet fra ref. / 6 /.
Beskrivelse av faste anlegg ble lagt på en fil og bestod av en enkel record-struktur. Det er to typer records: stasjoner (angitt med S i første kolonne) og blokkstrekninger (angitt med B i første kolonne). Begge typer har deretter en enkel beskrivelse av sporstrukturen. Denne består av
“navn på dette spor”, “navn på etterfølgende spor” og “navn på foregående spor”
Etterfølgende og foregående refererer til en definert retning. Både etterfølgende og foregående spor er nødvendig for å kunne representere overgang mellom enkeltspor og dobbeltspor.
Før de resterende dataelementene beskrives, vises de nødvendige data for strekningen Lillestrøm - Kløfta (tallene hentet fra ref. / 6 /)
S LILL BRØ1 2340 70 1440 1140 40 2 0 B BRØ1 BRØ2 LILL 2115 100 0 B BRØ2 LEIR BRØ1 1846 80 0 S LEIR BØRK BRØ2 1270 110 731 621 40 1 70 B BØRK FROG LEIR 1793 85 0 S FROG FRLI BØRK 1084 85 421 321 40 1 50 B FRLI LIND FROG 1623 100 0 S LIND ARTE FRLI 1317 120 796 696 40 1 70 B ARTE KLØF LIND 2697 120 0 S KLØF ARTE 1140 100 536 436 40 1 70
Navnene i sporstrukturen har kun 4 tegn, men de som er godt kjent på strekningen, vil kunne kjenne igjen de første bokstavene i navn på stasjoner og daværende holdeplasser på strekningen.
Etter sporstrukturen følger for stasjonene følgende dataelementer:
- lengde (mellom innkjørhovedsignalene) i m
- max hastighet i km/h avstand i m mellom ytterste sporveksler
- lengde i m av kryssingsspor
- max hastighet ved kjøring i avvik
- antall hovedspor (1 for enkeltspor, 2 for dobbeltspor)
- kryssingslåsingstid i sekunder
For beskrivelse av blokkstrekningene trengs kun
- lengde i m
- max hastighet i km/h
- hastighetsvariasjon i %
Signaler inngår ikke eksplisitt i beskrivelsen av faste anlegg for denne simuleringsmodellen, men det er implisitt forutsatt at det er et hovedsignal ved starten av hver blokkstrekning og stasjon, og at det er et tilhørende forsignal på en fast avstand. Vi kan derfor av tabellen ovenfor se at det er en blokkpost mellom de to første stasjonene, men ikke mellom noen av de andre.
Ved bruk av en modell med så små krav til data som vist i eksempelet ovenfor, vil man kunne gjøre de første simuleringene av en ny strekning allerede den første dagen man begynner arbeidet. Selv så enkle modeller kan gi forbausende gode resultater for relative problemstillinger når man er nøye med å vurdere resultatene i lys av forenklingene som er gjort (se kap. 6.4).
Ved bruk av en omfattende og detaljert modell vil det ta mange ukers eller kanskje måneders arbeid før man får gjort de første simuleringene.
Eksempel
Vi skal her vise et par eksempler på inngivelse av beskrivelsen av faste anlegg til en mer omfattende modell, hentet fra ref. / 7 /. Denne modellen har et større antall bilder for interaktiv registrering av data. Det vil føre alt for langt å gi noen fullstendig beskrivelse av databehovet og måten å registrere dette på. Her vises bare et par bilder angående data om signaler og sporseksjoner for å antyde detaljeringsgraden.
Man ser her for hver sporseksjon dataelementer som lengde, tilknytning til neste sporseksjon, betegnelse på tilhørende signal, siktavstand, antall aspekter i signalet m.m.
Noen modeller kan ha begrensninger når det gjelder hvor kompliserte sporsystemer som kan behandles, f.eks. vil ringbaner kunne medføre problemer for enkle modeller slik som modellen i det første eksempelet ovenfor.
Feil ved infrastrukturen har store konsekvenser for kapasitet og trafikkens kvalitet (kap. 5.1). Det er derfor viktig å kunne simulere også dette. Dette kan selvsagt alltid gjøres ved å endre på de aktuelle data, men da får man bare se konsekvensen av langvarige feil (hele tidsperioden i en enkelt simulering), og det medfører en del arbeid. Bedre er det med mulighet til å slå av og på visse typer tekniske feil eller å la dem oppstå med en viss sannsynlighet. Dette kan i prinsippet modelleres på samme måte som andre stokastiske forhold.
Togledelse
Dette er den delen hvor det er mest vanskelig å få en realistisk gjengivelse av virkeligheten fordi det hovedsaklig er menneskelige disponeringer som skal simuleres, og disse varierer fra person til person.
Dette gjenspeiler seg i de svært forskjellige måtene dette er gjort på i ulike simuleringsmodeller. Vi skal her nevne de vanligste måtene for å simulere togledelse:
- Modellen inneholder ikke egentlig noen modul for togledelse, men følger kun den oppsatte sporbruk gitt i ruteplanen. Modellen foretar altså ingen omdisponeringer “på egen hånd”. Når det ønskes en annen sporbruk, togrekkefølge o.l. enn det som er angitt i ruteplanen, må brukeren eksplisitt endre dette: interaktivt eller ved å foreta en helt ny kjøring. Dette blir ofte tidkrevende, men til gjengjeld kan man få akkurat den disponering man ønsker.
- Modellen inneholder faste prioriteringsregler, f.eks. “first come, first serve”, som brukeren ikke kan endre.
- Brukeren spesifiserer generelle prioriteringsregler, f.eks. basert på ulike togklasser, størrelse på forsinkelse o.l. (se f.eks. ref. / 8 /)
Ruteplan
Denne hoveddelen må som minimum inneholde identifikasjon av toget (f.eks. tognr.), begynnelse- og endestasjon (eventuelt bare retning hvis bare en enkel strekning simuleres) og steder underveis hvor toget skal stoppe. Videre må man ha starttid for hvert tog eller gjennomsnittlig frekvens for hver togtype. Sistnevnte tilfelle gjelder enkle modeller uten detaljert ruteplan eller når man vil gjøre vurderinger uten å være bundet opp til en konkret ruteplan. Man må også ha informasjon om hvilken togtype som skal brukes i hvert tog slik at modellen kan benytte de korrekte togdata.
Eksempel
Som et eksempel på hvor lite rutedata en enkel modell kan klare seg med, skal vi her vise beskrivelse av rutedata for samme modell som omtalt i eksempelet i kap. 6.2.2 (hentet fra ref. / 6 /).
Denne beskrivelsen av rutedata består dels av en enkel record-struktur (plassert sammen med faste data), dels av data som gis inn interaktivt. Det er to typer records: R-record for identifikasjon av togtype og H-record for beskrivelse av stoppesteder.
Record for identifikasjon består av følgende dataelementer:
- R togtype (tekst)
- retning (1=fra Oslo, 0=mot Oslo)
- statistikkdata (0: ingen statistikk)
Record for beskrivelse av stoppesteder består av følgende dataelementer:
- H stasjon eller blokkstrekning (4 karakterer som omtalt i eksempelet i kap. 6.2.2)
- midlere behandlingstid i s
- standardavvik for behandlingstid i s
Nedenfor gis et eksempel på hvordan dette kan se ut for lokaltog fra Oslo over samme strekning som beskrevet i eksempelet i kap. 6.2.2.
R LOKALTOG 1 0H LILL 60 30H LEIR 20 10H FROG 20 10H LIND 20 10H ARTE 15 5H KLØF 30 15
Så vises eksempel på en interaktiv sekvens (kun tallene gis inn) som angir hyppigheten av denne togtypen m.m.:
STARTVERDI FOR TILFELDIG TREKNING AV OPPHOLDSTIDER: 123 INTERVALL MELLOM HVER TOGAVGANG, MINUTTER (0 BETYR EN ENKLET TOGAVGANG): 60STARTVERDI FOR TILFELDIG TREKNING AV NESTE TOGAVGANG; VERDIEN 0 BETYR FAST FREKVENS, ELLERS ANTAS POISSONFORDELING: 0TIDSPUNKT FOR START, MINUTTER: 0
Utover dette må man for hver togtype i ruteplanen gi inn tilhørende togdata, som i denne modellen består av dataelementene toglengde, maksimalhastighet, akselerasjon, retardasjon og løsetid for bremser.
Dette er altså alt som trengs for å spesifisere lokaltog i stive timesruter i den ene retningen. For den andre retningen blir det helt tilsvarende. Øvrige togslag (hurtigtog, godstog) krever mindre arbeid fordi de har vesentlig færre stopp.
Detaljerte modeller vil typisk inneholde alle eller mesteparten av data i tjenesterutebøkene, dvs. avgangs- og ankomsttid (eller avgangs- og oppholdstid) for alle stasjoner/holdeplasser og sporbruk på hver stasjon. Hvis modellen har med materiellturnering, må det også angis hvilket tognr. som togets materiell skal fortsette i.
Detaljerte modeller har således et stort databehov også når det gjelder rutedata. JBV har en database over alle rutedata, slik at arbeidsmengden og tidsforbruket ved en simulering som inkluderer gjeldende ruteordning, kan reduseres hvis data kan overføres fra rutedatabasen til simuleringsmodellen.
Av andre data som kan være med her, skal nevnes en prioritetsklasse for toget, samt stokastiske parametere for både oppholdstider og startforsinkelse.
Realistisk størrelse og variasjon for oppholdstider er viktige i mange systemer. I tillegg til stokastiske variasjoner er det også noen systematiske variasjoner, f.eks. at oppholdstiden øker når toget er overfylt, forsinket eller bruker et annet spor enn det rutemessige. Ofte vil slike forhold ikke være modellert, og man bør da kompensere for dette ved å øke gjennomsnittsverdien for oppholdstidene og eventuelt også variasjonsområdet. Stokastiske forhold omtales noe mer i kap. 6.2.6.
Strømforsyning
Det er meget få modeller hvor strømforsyning er integrert i den totale simuleringsmodellen. En slik integrering fører nemlig til en sterkt økt kompleksitet med en mangedobling av regnetiden.
I en integrert modell er trekkraften avhengig både av hastighet og spenning. Dette modelleres ved flere trekkraft-kurver, for hvert sitt spenningsnivå, og det interpoleres mellom disse for å få den eksakte trekkraft. I hvert tidsskritt må det itereres på hele beregningen. Først beregnes trekkraft basert på spenningsnivåene fra forrige tidsskritt, og dette følges som vanlig av beregning av posisjon, hastighet m.m. for alle tog. Deretter beregnes strøm og spenning på alle aktuelle steder i kontaktledningen. Ved avvik (over et vist minimum) fra de verdier man startet iterasjonen med, må hele beregningsprosedyren gjentas for dette tidsskrittet, dvs. det må gjøres nok en iterasjon. Dette er hovedårsaken til den sterke økningen i regnetid. I tillegg bør man antagelig bruke kortere tidsskritt i en slik integrert modell.
En alternativ måte er å ha en separat modell for strømforsyningsanlegget. Inngangsdata til denne er da resultatfilen fra den ordinære simuleringsmodellen. Dermed blir det ingen vekselvirkning mellom tog og strømforsyning. Modellen for strømforsyningsanlegget fungerer da som en kontroll på at dette ikke blir overbelastet. Hvis denne modellen viser at spenningsforholdene blir uakseptable, må man endre noe i modellen av togsystemet slik at belastningen på strømforsyningsanlegget blir mindre.
De fleste modeller ignorerer imidlertid hele strømforsyningsanlegget.
Stokastiske elementer
En simuleringsmodell kan være helt deterministisk, men vanligvis er det å foretrekke at visse datatyper kan ha en tilfeldig varierende størrelse og eventuelt også forekomst fordi man i den virkelige verden observerer tilsynelatende tilfeldige variasjoner. Aktuelle stokastiske elementer er oppholdstider, forsinkelser, reaksjonstider, kjøretidstillegg, feil i tekniske forhold (bane, signal, tog).
Uten slike stokastiske muligheter vil man alltid ha usikkerheten om de valgte verdier på forsinkelser etc. er representative.
Som en fordel med rent deterministiske modeller hevdes at brukeren kan få nøyaktig de ønskede verdier på alle dataelementer, Men denne muligheten har man også på modeller med stokastiske elementer: det er bare å “slå av” bruken av dem, enten eksplisitt eller ved å sette variasjonen til 0.
De sannsynlighetsfordelinger som egner seg for variable som oppholdstid, forsinkelse, reaksjonstid o.l. er asymmetriske fordelinger med lengre “hale” mot høye verdier enn mot lave verdier. Erlang-fordelingen er et eksempel på en slik asymmetrisk sannsynlighetsfordeling som brukes i de nevnte sammenhenger.
For å kunne benytte slike muligheter må simuleringsmodellen ha en funksjon for å generere tilfeldige tall (“random number generator”). De generatorer som er i vanlig bruk, er strengt tatt (filosofisk sett) deterministiske fordi de genereres ved en matematisk formel. De kalles derfor “pseudo random number generator”. Brukeren gir en startverdi, og med samme startverdi får man alltid den samme sekvens av tall. Dette er en svært nyttig egenskap når man vil simulere virkningen av ulike alternativer fordi man da får den samme stokastiske variasjonen i alle alternativene.
Slike generatorer for tilfeldige tall er periodiske, dvs. at den samme sekvens kommer igjen etter en viss lengde. Perioden er imidlertid meget lang (avhenger bl.a. av datamaskinens interne representasjon av heltall) slik at dette sjelden medfører noe problem i praksis. Ved meget lange simuleringer bør man likevel undersøke hvilken periode den benyttede generator har.
Resultatpresentasjon
En simuleringsmodell beregner i utgangspunktet data av samme type som i prinsippet kan observeres/måles på det virkelige system, slik som avgangs-, ankomst-, passerings- og ventetider relatert til geografiske steder. Videre kan man da få kjøretider pr. tog osv. Dette blir normalt en stor mengde data som trenger videre bearbeiding, strukturering og ikke minst aggregering for å kunne være nyttig for brukeren.
Vanligvis vil en simuleringsmodell også inneholde en slik “etterbehandling” av resultater, enten som en integrert del av selve modellen eller som en “post-prosessor” som behandler de “rå” resultatfilene. F.eks. vil man kunne få ut resultater som:
- kjøretid fra start- til endestasjon
- forsinkelse til endestasjon
- utkjørt distanse
- antall restriktive signaler som medfører at toget må stoppe
- antall restriktive signaler som medfører bremsing, men ikke stopp
- tapt tid pga. restriktive signaler
- belegg av sporfelt, tid og antall ganger
Disse resultatene kan for togenes del gis pr. tog, pr. tog-gruppe, totalt, i gjennomsnitt, for de mest forsinkede togene osv., avhengig av hva som er medtatt i den enkelte modell. For simuleringer hvor visse inngangsdata er stokastiske, er det også viktig at modellen gir spredningsverdier av resultatene, f.eks. standardavvik. Dette er nødvendig for å kunne gjøre statistiske tester på en enkel måte.
For å kunne trekke fornuftige slutninger på grunnlag av resultatene fra modellen må man vurdere forutsetningene som eksplisitt er lagt inn og som implisitt ligger i modellens konstruksjon, jfr. kap. 6.4.
Mulighet for å få grafisk rute over den aktuelle kjøring er også vanlig, og dette er særlig nyttig på enkeltspor fordi man da lett ser hvordan det er prioritert ved konflikter o.l. Følgende figur viser et eksempel på slik utskrift, hentet fra ref. / 7 /.
Figur 25: Eksempel på grafisk fremstilling av simulert trafikk.
De signaler eller sporfelt hvor mange tog taper tid (de siste punktene i listen ovenfor), er ofte nyttige for å finne flaskehalser i systemet fordi slik informasjon indikerer de steder hvor det oftest er konflikter mellom togene. Dette representerer potensielle steder for utbyggingstiltak. Følgende figur viser et eksempel på en slik utskrift, også hentet fra ref. / 7 /.
Figur 26: Eksempel på utskrift av sporseksjoner hvor tog må stoppe eller bremse.
Gjennomføring av en simuleringsstudie
Det første som bør gjøres er å klarlegge problemstillingen som man vil undersøke (jfr. kap. 6.1). Videre må man se på hvordan bruk av en simuleringsmodell kan bidra til å besvare problemstillingen.
På grunnlag av problemstillingen må det bestemmes hvilke forutsetninger som skal legges til grunn for simuleringene, og hvilke forenklinger man derfor kan gjøre. Dette må så vurderes opp mot de forutsetninger og forenklinger som ligger i den aktuelle simuleringsmodellen.
Innsamling og registrering av de nødvendige data vil ofte være en tidkrevende oppgave, spesielt ved første gangs simulering av en strekning fordi man da må ha med alle data om faste anlegg. Ved senere simuleringer vil disse kunne brukes om igjen. Mulighet for automatisk overføring fra andre datasystemer (data for faste anlegg og ruteplan) representerer en stor lettelse i dette arbeidet.
Hvis oppgaven er å simulere en eksisterende strekning, bør man alltid simulere dagens situasjon først (“0-alternativet”). Dette er viktig, både som en kontroll av inndata (og eventuelt modell) og som et utgangspunkt for de senere kjøringer, som f.eks. kan være å studere virkningen av alternative utforminger. Ved sammenlikning av flere alternativer er det ofte greitt å se på forskjellen fra 0-alternativet, samt på forskjeller mellom andre alternativer innbyrdes.
For hvert alternativ man vil studere (inkl. et eventuelt 0-alternativ), bør det foretas kjøringer med noe ulike parametere. Det kan f.eks. være aktuelt å se på små og store startforsinkelser og/eller oppholdstider, feilsituasjoner på teknisk utstyr o.a. Man får da se hvor følsom modellen er for slike endringer i inngangsdata. Hvis endringene i resultatene er så store at man ville ha valgt et annet alternativ når man endrer slike inngangsdata, tyder det på at valg av alternativ er løst fundert, eller at det er liten forskjell mellom alternativene. I det videre arbeid må man da simulere et representativt utvalg av slike parametere for hvert alternativ.
Når man skal vurdere resultatene fra en simuleringsmodell og trekke konklusjoner på grunnlag av disse, må man også trekke inn de forutsetninger og tilnærmelser som er gjort ved konstruksjon av modellen og ved valg av inngangsdata. Det er her en klar forskjell mellom relativ bruk (valg mellom spesifiserte alternativ) og absolutt bruk (avgjøre om ett gitt alternativ er godt nok eller ikke).
Absolutt bruk vil ofte kreve en mer nøyaktig modell og en grundigere vurdering av modellens tilnærmelser og virkemåte enn relativ bruk. Det er ofte slik at tingene “glir” litt lettere i en simuleringsmodell enn i virkeligheten, fordi det alltid kan forkomme spesielle forhold som ikke er tatt hensyn til i modellen. F.eks. kan man nevne slike i og for seg enkle ting som at en del mennesker gjerne tenker seg om litt ekstra i vanskelige situasjoner, eller at noen lett gjør feilvurderinger da. “Menneskene” i en simuleringsmodell er mer rasjonelle og gjør alltid de riktige tingene uten betenkningstid utover eventuelle innlagte reaksjonstider. Derfor må man nøye vurdere om modellen har vært for “snill” eller “flink” før man trekker konklusjoner angående den kvalitet man kan vente seg i den virkelige trafikkavviklingen.
Ved relativ bruk er dette enklere. Da er det ofte tilstrekkelig å kontrollere at tilnærmelser og virkemåte ikke favoriserer det valgte alternativet, m.a.o. at modellen er nøytral eller konservativ m.h.p. valg av alternativ i den aktuelle situasjonen. Mange av forskjellene mellom modell og virkelighet vil gi omtrent samme virkning i de ulike alternativene, og de vil dermed ha liten innflytelse på valg av alternativ. Andre forskjeller vil være slik at man vet at de favoriserer et alternativ, f.eks. er det vanligvis slik at toglederens arbeid blir enklere med økende utbygging av infrastrukturen (f.eks. ved overgang fra tradisjonelle stasjoner til stasjoner med samtidig innkjøring eller fra enkelt til dobbelt spor). Hvis man da ut fra simuleringsresultatene vil velge det alternativ som gjør toglederens arbeid enklere, så vil dette avviket mellom modell og virkelighet styrke konklusjonen. Hvis man på den annen side vil velge et alternativ som f.eks. gjør toglederens arbeid vanskeligere, må man få disse forhold med i modellen eller forsøke å korrigere resultatene for dette avviket mellom modell og virkelighet.
Hvis resultatene skal vurderes statistisk, må de enkelte simuleringer for ett alternativ være stokastisk uavhengige. Valg av forskjellige startverdier til generatoren for tilfeldige tall vil normalt sikre dette. Antall nødvendige enkeltkjøringer av hvert alternativ avhenger av statistisk metode og signifikansnivå. Man kan begynne med få (5 - 10) kjøringer pr. alternativ og om nødvendig øke antallet inntil man får signifikante forskjeller. Jo mindre forskjeller man ønsker å detektere, desto flere kjøringer må til. Med en kjøring menes her en simulering av den aktuelle tidsperiode (dag, rushtid).
For å slippe å få alt for mange kjøringer er det viktig at de samme startforsinkelser og andre stokastiske parametere benyttes en gang på samtlige alternativ man skal undersøke. Resultatene kan da grupperes i sett hvor hvert sett inneholder en kjøring for hvert alternativ og med de samme stokastiske forhold. Dette gir vesentlig mindre varians enn å velge nye stokastiske verdier for hver enkelt kjøring.
Også ved absolutt bruk kan man gjøre statistiske vurderinger. Man må da se på resultatene fra modellen i forhold til fastsatte krav til trafikkavviklingen. Her kan det f.eks. brukes statistiske metoder av samme type som ved kvalitetskontroll i serieproduksjon.
Referanser.
- UIC-kodex 405E “Methode zur Ermittlung der Leistungsfähigkeit von Strecken”
- A. Cardani: “Multiple Aspect Signalling (British Practice)”, The Institution of Railway Signal Engineers, no14; Reading, 1963.
- R. Pope: “Signalling the Layout, British Railways Practice”, The Institution of Railway Signal Engineers, no27; Reading, 1973.
- S. Skartsæterhagen og T. Vasset: “Kapasitetsmessig virkning av samtidig innkjøring på stasjoner.”, NSB-teknikk 1984.
- G. Potthoff: “Verkehrströmungslehre, Band1, Die Zugfolge auf Strecken und in Bahnhöfen”; Transpress, Berlin, 1970.
- FoU-prosjekt D18: Kapasitetsutbygging på nærtrafikkstrekninger. Metodikk for kapasitetsundersøkelser og utviklingsplan for strekningen Lillestrøm - Eidsvoll. Bilagsrapport, bilag V, NSB 1979.
- Comreco Rail Ltd: RailPlan Simulation System. Product Overview.
- R. Moen: “Simulering av togbevegelser på større stasjoner.”, hovedoppgave i kybernetikk, Universitetet i Oslo, 1974.