Utledning kurveveksler: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (24 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
== Utledning, formel for radier, kurveveksel == | == Utledning, formel for radier, kurveveksel == | ||
Her følger utledning av formler for radius i kurveveksler, gitt at dene ene av de to radiene er kjent. Formelgrunnlaget baserer seg på at stigningen i vekslene holdes konstant når den enkle vekselen bøyes. | |||
I figuren under vises geometri for en enkel sporveksel med lang kurve og en utoverbøyd kurveveksel. | I figuren under vises geometri for en enkel sporveksel med lang kurve og en utoverbøyd kurveveksel. | ||
| Linje 32: | Linje 34: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R(r-x | R(r-x-rcos(\alpha)-xcos(\alpha)) = (rx+x^2)(1+cos(\alpha)) | ||
</math> | </math> | ||
</div> | </div> | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R\left | R\left (r(1-cos(\alpha))-x(1+cos(\alpha))\right ) = (rx+x^2)(1+cos(\alpha)) | ||
</math> | </math> | ||
</div> | </div> | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R\left | R\left (r\cdot\frac{1-cos(\alpha)}{1+cos(\alpha)}-x\right ) = x(r+x) | ||
</math> | </math> | ||
</div> | </div> | ||
| Linje 49: | Linje 51: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
tan(\alpha/2) | tan^2(\alpha/2)=\frac{1-cos(\alpha)}{1+cos(\alpha)} | ||
</math> | </math> | ||
</div> | </div> | ||
| Linje 56: | Linje 58: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R\left ( | R\left (\frac{r}{x}\cdot tan^2(\alpha/2)-1\right ) = r+x | ||
</math> | |||
</div> | |||
</br> | |||
Fra geometrien i den enkle vekselen, kan vi nå innføre: | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
tan(\alpha/2) = \frac{t}{r_0} | |||
</math> | |||
</div> | |||
</br> | |||
Merk at dette er en tilnærming som kun er gyldig når stigningen i vekselen kan ses på som liten. | |||
</br></br> | |||
Ved å også benytte at | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
tan(\alpha/2) = \frac{x}{t} | |||
</math> | |||
</div> | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
\frac{t}{r_0} = \frac{x}{t} | |||
</math> | |||
</div> | |||
får vi | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
R(\frac{r\cdot r_0}{t^2}\cdot\frac{t^2}{r_0^2}-1) = r+\frac{t^2}{r_0} | |||
</math> | |||
</div> | |||
og til slutt | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
R = \frac{r\cdot r_0+t^2}{r-r_0} | |||
</math> | |||
</div> | |||
</br></br> | |||
Denne ligningen kan også løses for <i>r</i>, og uttrykket blir da | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
r = \frac{R\cdot r_0+t^2}{R-r_0} | |||
</math> | |||
</div> | |||
</br></br></br> | |||
=== Alternativ løsning === | |||
En mer nøyaktig sammenheng mellom <i>R</i> og <i>r</i> kan oppnås ved å benytte følgende sammenhenger, som er basert på at vekselen ikke endrer lengde når den bøyes: | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
2t=R\beta | |||
</math> | |||
</div> | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
r_0\alpha=r\xi | |||
</math> | |||
</div> | |||
</br> | |||
og enten | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
\alpha=\beta+\xi | |||
</math> | |||
</div> | |||
for utoverbøyd veksel, eller | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
\alpha=\xi-\beta | |||
</math> | |||
</div> | |||
for innoverbøyd veksel. | |||
</br></br> | |||
Dette gir | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
R = \pm\frac{2r_0\cdot tan(\alpha/2)}{\alpha\cdot(1-\frac{r_0}{r})} | |||
</math> | |||
</div> | |||
for henholdsvis utoverbøyd og innoverbøyd veksel.</br></br> | |||
Dersom det løses for <i>r</i>, blir resulterende ligning | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
r = \frac{r_0}{1\mp\frac{2r_0\cdot tan(\alpha/2)}{R\alpha}} | |||
</math> | |||
</div> | |||
for henholdsvis utoverbøyd og innoverbøyd veksel.</br> | |||
=== Lokale koordinater === | |||
Lokale koordinater kan også beregnes fra noen geometriske betraktninger. | |||
FEIL | |||
[[Fil:Enkel med skinner.jpg|600px|rammeløs|sentrer|Enkel veksel med skinnekryss]] | |||
</br> | |||
Spissvinkelen til skinnekrysset, <math>\phi</math>, kan beregnes ved | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
cos(\phi) = \frac{r_0-s/2}{r_0+s/2} | |||
</math> | |||
</div> | |||
</br> | |||
Eventuelt kan dette skrives | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
tan(\phi) = \frac{2\cdot \sqrt{2r_0\cdot s}}{2r_0-s} | |||
</math> | </math> | ||
</div> | </div> | ||
Siste sideversjon per 20. apr. 2021 kl. 09:48
Utledning, formel for radier, kurveveksel
Her følger utledning av formler for radius i kurveveksler, gitt at dene ene av de to radiene er kjent. Formelgrunnlaget baserer seg på at stigningen i vekslene holdes konstant når den enkle vekselen bøyes.
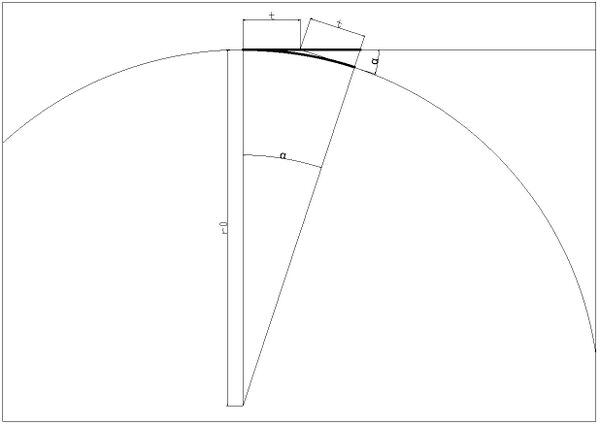
I figuren under vises geometri for en enkel sporveksel med lang kurve og en utoverbøyd kurveveksel.
Siden vinkelen er liten, antas t å være tilnærmet lik både før og etter bøying av den enkle vekselen. Ved å benytte cosinussetningen:
oppnås følgende sammenheng mellom radier og vinkel, :
Videre bearbeiding av denne ligningen gir:
Ved å benytte den trigonometriske identiteten:
gir dette videre:
Fra geometrien i den enkle vekselen, kan vi nå innføre:
Merk at dette er en tilnærming som kun er gyldig når stigningen i vekselen kan ses på som liten.
Ved å også benytte at
får vi
og til slutt
Denne ligningen kan også løses for r, og uttrykket blir da
Alternativ løsning
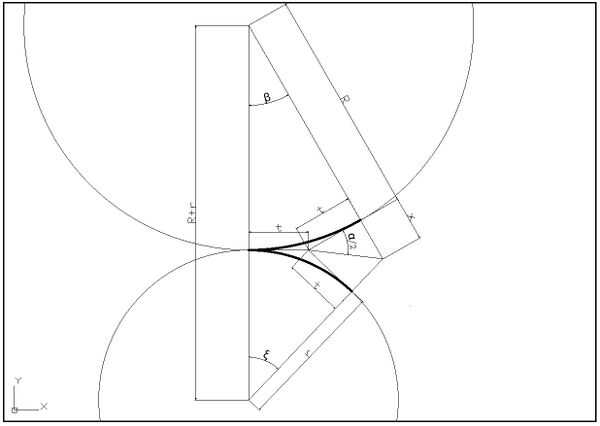
En mer nøyaktig sammenheng mellom R og r kan oppnås ved å benytte følgende sammenhenger, som er basert på at vekselen ikke endrer lengde når den bøyes:
og enten
for utoverbøyd veksel, eller
for innoverbøyd veksel.
Dette gir
for henholdsvis utoverbøyd og innoverbøyd veksel.
Dersom det løses for r, blir resulterende ligning
for henholdsvis utoverbøyd og innoverbøyd veksel.
Lokale koordinater
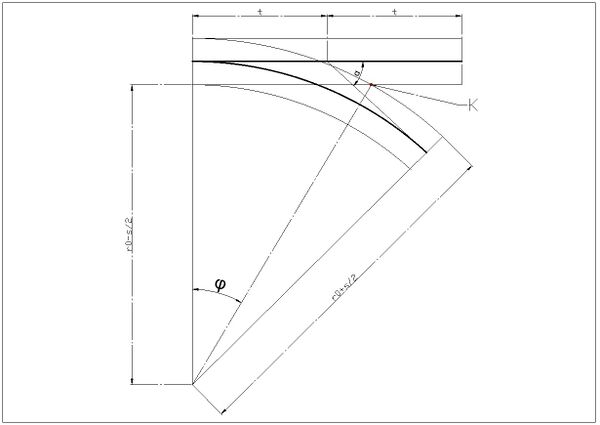
Lokale koordinater kan også beregnes fra noen geometriske betraktninger. FEIL
Spissvinkelen til skinnekrysset, , kan beregnes ved
Eventuelt kan dette skrives