Sporets trasé/Sporgeometri
Innhold
1 Innledning og grunnleggende definisjoner
1.1 Historikk
De eldre jernbanesporene i Norge ble formet etter terrenget på en tid da hensynet til massebalansen ble vektlagt. Krutt var dyrt, og det kostet også mye å flytte på massene. Men med en hastighet på 30 km/h og kurveradier på 250 m, lot bygging av nyanlegg seg gjøre uten de helt store inngrepene. I dag gjelder fortsatt denne utformingen for de fleste strekningene i landet, men kravet til hastighet har naturlig nok økt i takt med teknisk utvikling og moderne transporttilbud. Den avgjørende størrelsen i dag blir derfor dimensjonerende hastighet, som blant annet setter høye krav til sporets geometri.
Når en løsning er valgt for en togtrasé, vil ulike hensyn avsette en del tekniske fastpunkter, det vil si punkter traséen må passere. Med trasering/ teknisk linjeføring menes den geometriske utformingen av linjen mellom de tekniske fastpunktene, og krav til utformingen settes av sporets geometri, hastighetsbetraktninger og de enkelte traseringsparametrene, foruten hensyn til det rullende materiell, som aksellast, trekkraft og kjøremotstand.
For å beskrive traséen teknisk sett, skiller vi mellom horisontal- og vertikal-geometri. De fleste geometriske størrelser betraktes i planet, selv om den faktiske traséen på alle måter ligger i rommet. Her beskrives krumning, overganger, ulik kurvatur og helning på tvers av sporet. Vertikalkurvaturen betraktes som et langsliggende profil, hvor traséen litt forenklet sagt endrer seg mellom stigning og fall. Uansett er denne geometrien mye enklere enn hos horisontalkurvaturen og betraktes separat. Der komplisert horisontalkurvatur forekommer er det også viktig at vertikalkurvaturen ikke innebærer store endringer.
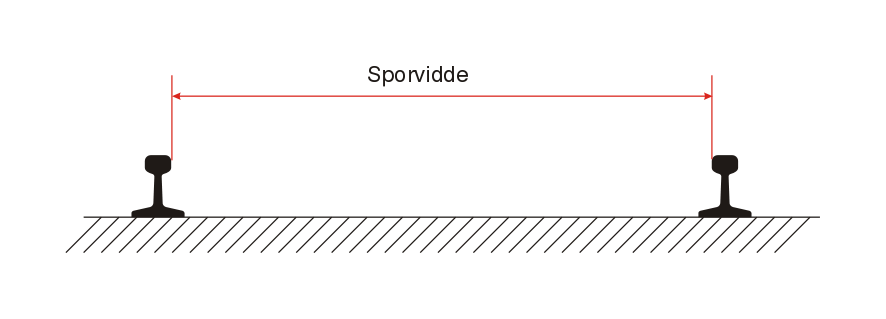
1.2 Sporvidde
Definisjon: Sporvidden s er den vinkelrette, horisontale avstanden mellom kjørekanten til de to skinnestrengene, målt 14 mm under skinnehodets topp.
I Norge er sporvidden satt lik 1435 mm. Der denne sporvidden er anordnet betegnes sporet normalspor. Bredere spor kalles bredspor og smalere spor kalles smalspor.
Når sporvidden s inngår i geometriberegninger, brukes imidlertid en annen sporvidde, s = 1500 mm.
Mer om sporvidde på no.wikipedia.org/wiki/Sporvidde
1.3 Overhøyde
Definisjon: Overhøyden h er høydeforskjellen mellom skinnestrengene i forhold til horisontalplanet, målt vinkelrett på sporet.
Overhøyden angir hvilken helning sporplanet (kjøreflaten) har og tilsvarer det som kalles dossering for vei. Overhøyden angis vanligvis i millimeter, men kunne også vært oppgitt som en vinkel med horisontalplanet (β).
2 HORISONTALKURVATUR
2.1 Kurver i horisontalplanet
I en alminnelig trasé har vi tre elementer: rettlinjer, sirkelkurver og overgangskurver. Sirkelkurvene angis ved radius R som er radius for spormidt. Eldre linjer i Norge har radius helt ned til R = 180 m, som utgjør en svært krapp sirkelkurve. Med dette forstår vi at kurvatur er en av de viktigste faktorene når hastigheten skal imøtekomme dagens krav til effektiv transport. Tabeen nedenfor viser en kurvefordeling for ulike eksisterende baner i Norge:
| R ≤ 300 m | 300 m < R ≤ 500 m | 500 m < R ≤ 1100 m | R > 1100 m | Rettstrekning | Minste radius | |
|---|---|---|---|---|---|---|
| Østfoldbanen, vestre linje | 2 % | 14 % | 13 % | 20 % | 51 % | 200 m |
| Østfoldbanen, østre linje | 3 % | 17 % | 17 % | 16 % | 46 % | 239 m |
| Dovrebanen | 8 % | 12 % | 17 % | 23 % | 40 % | 225 m |
| Kongsvingerbanen | 0 % | 3 % | 23 % | 20 % | 54 % | 257 m |
| Rørosbanen | 7 % | 13 % | 16 % | 14 % | 50 % | 189 m |
| Nordlandsbanen | 3 % | 20 % | 17 % | 19 % | 41 % | 210 m |
| Gjøvikbanen | 20 % | 15 % | 16 % | 18 % | 31 % | 230 m |
| Bergensbanen | 12 % | 12 % | 15 % | 18 % | 43 % | 160 m |
| Sørlandsbanen | 12 % | 18 % | 13 % | 15 % | 41 % | 243 m |
| Vestfoldbanen | 9 % | 11 % | 11 % | 25 % | 43 % | 180 m |
| Solørbanen | 1 % | 3 % | 7 % | 28 % | 60 % | 245 m |
| Roa - Hønefoss | 18 % | 21 % | 13 % | 21 % | 26 % | 238 m |
| Raumabanen | 7 % | 7 % | 21 % | 21 % | 43 % | 259 m |
| Meråkerbanen | 9 % | 16 % | 18 % | 15 % | 42 % | 275 m |
| Namsosbanen | 5 % | 14 % | 13 % | 23 % | 45 % | 250 m |
| Randsfjordbanen | 5 % | 22 % | 21 % | 15 % | 37 % | 196 m |
| Flåmsbana | 51 % | 5 % | 8 % | 1 % | 35 % | 130 m |
| Spikkestadbanen | 7 % | 12 % | 14 % | 22 % | 45 % | 269 m |
| Arendalsbanen | 32 % | 13 % | 7 % | 18 % | 30 % | 210 m |
| Ofotbanen | 24 % | 21 % | 14 % | 8 % | 33 % | 250 m |
| Drammenbanen | 1 % | 11 % | 12 % | 24 % | 51 % | 246 |
| Totalt 1) | 8 % | 15 % | 15 % | 19 % | 43 % | 130 m |
- Totalsum for banene nevnt ovenfor. Øvrige baner i Norge (eksempelvis sidespor som Numedalsbanen eller museumsbaner som Krøderbanen) er ikke inkludert.
2.2 Rettlinjer
Rettlinjer er som ordet sier rette linjer i traséen. De kan også beskrives som sirkelkurver med radius lik uendelig. Rettlinjen kan tilstøte både overgangskurven og sirkelkurven, sistnevnte ofte på stasjoner og i sidespor.
Rettlinjen som traseringselement er relativt uproblematisk. Geometrisk sett er det ingen hastighetsbegrensninger på rettlinjen (men mange andre faktorer kan være begrensende, se for eksempel Hastighetsberegninger). Det eneste kravet sporgeometrien setter til rettlinjen er at den ikke må være for kort:
- Mellom motsattrettede sirkelkurver med små radier er det fare for ombufring (se avsnittet bufferoverdekning i kontrakurve) dersom ikke rettlinjen derimellom er over en viss lengde
- Mellom kurver uten overgangskurver bør det være en rettlinje av en viss lengde for å hindre at passasjerene opplever flere brå bevegelser i vognen rett etter hverandre.
- Generelt er det en fordel for passasjerenes komfort at vognen befinner seg minst 1-2 sekunder i hver rettlinje.
| Normale krav [m] | Minste krav [m] |
|---|---|
| 0,5 V | 0,25 V |
(krav om minste lengde for avsnitt med konstant krumning, Teknisk regelverk 2014)
Dette kravet sørger for at gjennomkjøringstiden for hvert element blir minimum 0,9 sekunder (0,25 x 3,6) for minste krav og 1,8 sekunder for normale krav.2.3 Sirkelkurver
En sirkelkurve er en del av en sirkel, det vil si en kurve som har konstant krumming langs hele kurven. Sirkelkurvens krumming κ er definert utfra radien R ved κ = 1/R.
For å beskrive sirkelkurvens egenskaper må vi først ta en del fysiske størrelser i betraktning.
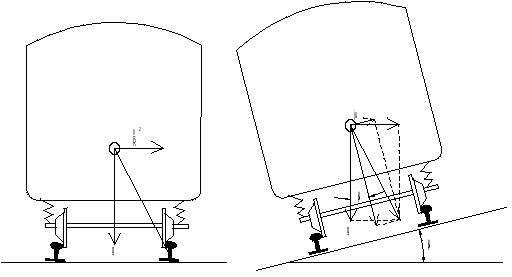
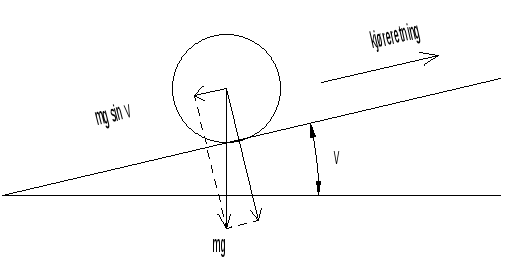
2.3.1 Sentripetalakselerasjon og sideakselerasjon
Dersom vi kjører i en sirkelkurve i konstant hastighet, har vi to konstante akselerasjoner (se figur 1): Tyngdens akselerasjon g som virker vertikalt nedover og sentripetalakselerasjonen [math]\frac{v^2}{R}[/math] (ofte kalt a i fysikkbøker) rettet innover mot kurvens sentrum. For en passasjer føles det imidlertid som om akselerasjonen er rettet ut av kurven. Kraften på grunn av denne akselerasjonen omtales gjerne som sentrifugalkraft - en størrelse som i fysikken regnes som en fiktivkraft. Vi skal imidlertid i det følgende bruke sideakselerasjon med benevning j om nettopp denne størrelsen, som dermed er rettet motsatt vei av den virkelige sentripetalakselerasjonen,
| [math]j = \frac{v^2}{R}[/math] | (1) |
I kurver med overhøyde er det akselerasjonens komponenter parallelt med vogngulvet som er avgjørende for passasjerenes komfort.
Utfra figur 1 kan vi se at gravitasjonens komponent langs vogngulvet er:
| [math]g' = g\cdot\sin\beta = g\cdot\frac{h}{s}[/math] | (2) |
På samme måte finner vi sideakselerasjonens komponent langs vogngulvet:
| [math]j' = j\cdot\cos\beta [/math] | (3) |
Fordi β er liten, kan vi sette cos β ≈ 1 og j' ≈ j, det vil i praksis si at vi regner sideakselerasjonen for å virke parallelt med vogngulvet.
Tyngdekraftens komponent langs vogngulvet, g', virker i motsatt retning av j'. Det betyr at den følte sideakselerasjonen reduseres. Vi definierer begrepet ukompensert sideakselereasjon som j' minus g':
| [math]j_u = \frac{v^2}{R} - g\cdot\frac{h}{s}[/math] | (4) |
2.3.2 Hastighet i sirkelkurven
Dersom vi snur om på (4) kan vi få et uttrykk for hastigheten:
[math]v = \sqrt{R \left(\frac{gh}{s}+j_\text{u}\right)}[/math]
Ved å sette en maksimalverdi for ju får vi et uttrykk for maksimal hastighet:
| [math]v_\text{maks} = \sqrt{R \left(\frac{gh}{s}+j_\text{u,maks}\right)}[/math] [m/s], | (5) |
der grenseverdien ju,maks har ulik verdi avhengig av togtype, kurveradius, banestandard eller andre parametre fastsatt av den enkelte forvaltning. Verdien av ju,maks ligger vanligvis i intervallet 0,5 - 1,5 m/s2.
For spor uten overhøyde reduseres (5) til
[math]v_\text{maks} = \sqrt{R \cdot j_\text{u,maks}}[/math] [m/s],
der ju er lik j fordi gravitasjonen ikke kompenserer noe av sideakselerasjonen.
[math]v_\text{maks} = \sqrt{350 \left(\frac{9,81 \cdot 140}{s}+0,98\right)} \approx 25,8 \;\text{m/s}[/math]
For å få hastigheten i kilometer per time istedenfor meter per sekund, multipliseres den med 3,6:
[math]V_\text{maks} = v_{maks} \cdot 3,6 \approx 93 \text{km/h}[/math]
(Liten v brukes i dette kapitlet alltid for hastighet i m/s og stor V for hastighet i km/h.)
Dersom man justerer overhøyden til h = 0 mm i samme sirkelkurve, blir hastigheten også lavere;
[math]v_\text{maks} = \sqrt{350 \cdot 0.98} \approx 18,5 \;\text{m/s}[/math],
som tilsvarer ca 67 km/h.
2.3.3 Likevektshastighet og teoretisk overhøyde
For en kurve med en gitt overhøyde finnes det en hastighet v slik at sideakselerasjonen er like stor som gravitasjonens komponent langs vogngulvet,
| [math]\frac{v^2}{R} = g\cdot\frac{h}{s}[/math] | (6) |
I dette tilfellet er ukompensert sideakselerasjon på vognen lik null. Denne hastigheten kalles likevektshastighet. Ved å løse for v, ser vi at likevektshastigheten er gitt ved
| [math]v_\text{likevekt} = \sqrt{R\cdot g \cdot\frac{h}{s}}[/math] | (7) |
Den overhøyden som gir likevektshastighet, kalles teoretisk overhøyde. Ved å løse (6) for h isteden, får vi
| [math]h_\text{teor} = \frac{s\cdot v^2}{g\cdot R}[/math] | (8) |
[math]v_\text{likevekt} = \sqrt{600\cdot 9,81 \cdot\frac{100}{1500}} \approx 19,8 \text{ m/s} \approx 71 \text{ km/h}[/math].
Dersom man ønsker å øke likevektshastigheten til 80 km/h (tilsv. 22,22 m/s), kan man regne ut hvor stor overhøyden da må være:
[math]h_\text{teor} = \frac{1500\cdot (22,22)^2}{9,81\cdot 600} \approx 125,8 \text{ mm}[/math]
For persontrafikken er hastigheten som regel større enn likevektshastigheten, og da vil gravitasjonens komponent parallelt med sporplanet bare kompensere for deler av sideakselerasjonen, som er akkurat det (4) viser
| [math]\frac{v^2}{R} - g\cdot\frac{h}{s} = j_u[/math] |
Hvis hastigheten er mindre enn likevektshastigheten, blir ju negativ, det vil si at den er rettet innover i kurven. Det blir en overkompensering, eller overskuddssideakselerasjon. Dette er ofte tilfellet for godstog som trafikkerer spor beregnet for blandet trafikk, eller ved saktekjøringer. Ved full stans virker kun gravitasjonens komponent, og dette setter grenser for hvor stor overhøyden kan være. I Norge er maksimal overhøyde satt til hmaks = 150 mm, i tråd med det som er mest vanlig hos de fleste forvaltningene i Europa.
En annen vinkling på den ukompenserte sideakselerasjonen er at overhøyden ikke er stor nok for den aktuelle hastigheten. Vi definerer manglende overhøyde som I = hteor - h, det vil si
| [math]I = \frac{sv^2}{gR} - h[/math] | (9) |
Multipliserer vi ut uttrykket for ukompensert sideakselerasjon (4), med s/g, får vi et utrykk for manglende overhøyde i forhold til den ukompenserte sideakselerasjonen:
| [math]I = \frac{s}{g}\cdot \frac{v^2}{R} - h = \frac{s}{g} \cdot j_u[/math] | (10) |
Innsatt med verdier for s og g får vi at I ≈ 153 [math]\cdot[/math] ju. Manglende overhøyde er altså et begrep som gir akkurat samme informasjon som den ukompenserte sideakselerasjonen, men i jernbanesammenheng er det mer vanlig å bruke manglende overhøyde.
[math]v_\text{maks} = \sqrt{\frac{gR}{s} \cdot (h+I_\text{maks})}[/math] (11)
Setter inn kjente størrelser og multipliserer med 3,6 for å få hastighet i km/h:
[math]V_\text{maks} = 0,291\cdot \sqrt{R (h+I_\text{maks})}[/math] (12)
Kan da regne ut eksempel 2 på nytt med den forenklede formelen ([math]j_\text{u,maks} = 0,98 \text{ m/s}[/math] tilsvarer [math]I_\text{maks} = 150 \text{ mm}[/math]) og se at svaret blir det samme:
[math]V_\text{maks} = 0,291\cdot \sqrt{350\cdot (140+150)} = 93 \text{ km/h}[/math]
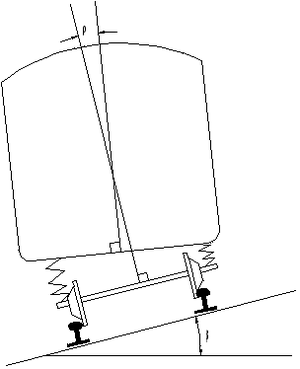
2.3.4 Rullvinkel
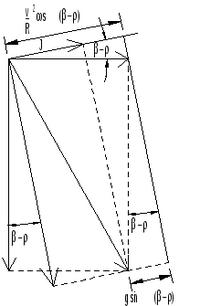
Den ukompenserte sideakselerasjonen (ju) gjør at vognkassens fjæranordning blir usymmetrisk belastet, og vogngulvet får en vinkel med sporplanet, som vist på figur 2. Denne vinkelen kalles rullvinkel eller rullingsvinkel. Rulling av vognkassen vil delvis oppheve effekten av overhøyden når vognen kjøres med større fart enn likevektshastigheten.
Som følge av rullingen blir den ukompenserte sideakselerasjonen som passasjerene merker større enn ju. På samme måte som i sentripetalakselerasjon og sideakselerasjon kan vi finne sideakselerasjonens komponent langs vogngulvet (J) og gravitasjonens komponent vinkelrett på vogngulvet (g''). Akselerasjonen J kalles effektiv sideakselerasjon eller merkbar ukompensert sideakselerasjon. Den er et bedre mål for kjørekomfort enn ju, men den er avhengig av type materiell. Rullvinkelen er vanligvis proporsjonal med ju:
| [math]J = (1+r)\cdot j_u[/math], | (13) |
der r er rullvinkelkoeffisienten. Den kan beregnes eller fastlegges ved forsøk.
For vanlige normalsporede gods- og personvogner ligger rullvinkelkoeffisienten i størrelsesorden 0,1-0,6. For NSBs B7-vogner er r = 0,2. For krengetog blir situasjonen motsatt, i og med at vogna lener seg innover i stedet for utover i kurven. Rullvinkelkoeffisient blir altså negativ. For NSBs krengetog (Signatur) ligger rullvinkelkoeffisienten på ca. r = -0,55 og for SJs X2000 er r = -0,7.
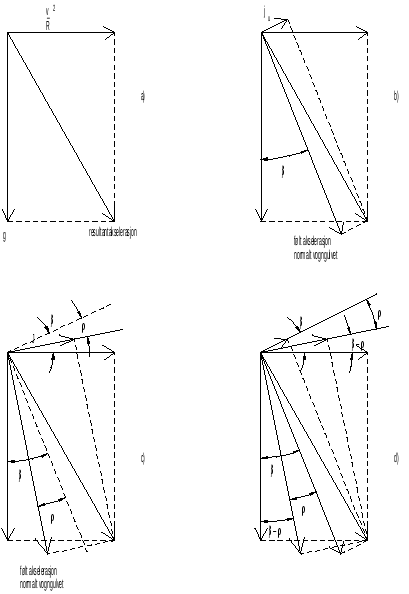
Ved å betrakte figur 4, kan vi utlede sammenhengen mellom rullvinkelkoeffisienten r og rullvinkelen ρ fra ligning 13:
| [math]\frac{v^2}{R}\cdot\cos (\beta-\rho) - g\cdot\sin (\beta-\rho) = j_u (1+r) = J[/math] | (14) |
Jamfør tidligere tilnærminger, kan vi sette cosβ ≈ cosρ ≈ 1. Med sinβ = h/s kan vi med litt regning komme fram til følgende uttrykk for rullvinkelkoeffisienten:
| [math]r = \frac{\sin\rho}{j_u}\left(j_u \cdot\frac{h}{s}+g\cdot\frac{h^2}{s^2}+g\right)[/math] | (15) |
Uttrykket kan imidlertid forenkles gjennom tilnærming. På grunn av at rullvinkelen er liten, kan vi tilnærme sinρ med ρ . Dessuten er de to første leddene i parentesen i formel 15 så små at vi kan utelate dem for deretter å oppveie dem ved å sette tyngdeakselerasjonen g = 10. Dermed får vi et svært enkelt uttrykk for rullvinkelkoeffisienten:
| [math]r = \frac{10\cdot\rho}{j_u}[/math] | (16) |
der ρ er i radianer.
Likning 16 innsatt i utgangslikningen gir effektiv sideakselerasjon som funksjon av rullvinkelen:
| [math]J = j_u+10\rho[/math] | (17) |
Når denne forenklede formelen tas i bruk, må det nevnes at dynamiske bidrag er utelatt. Disse vil i praksis øke den effektive sideakselerasjonen J ytterligere, men beregningsmessig er det alltid ju som er traseringselementet. Det kan allikevel nevnes at J til en viss grad er tatt hensyn til i regelverket for mange forvaltninger ved at det benyttes ulike traseringsparametre for ulike togtyper.
Uten å gå inn på beviset her, kan det vises at rullvinkelen i stor grad er proporsjonal med sideakselerasjonen, slik at det finnes en konstant c som gir ρ = c ju . I ligning 16 får vi da eliminert hele sideakselerasjonen ju , og rullvinkelkoeffisienten blir en konstant for hvert enkelt rullende materiell. De avgjørende elementer blir da lastens masse og plassering, egenskaper og plassering til vognas fjæringssystem.
2.3.5 Grenseverdier
Ved fastsettelse av grenseverdien(e) ju,maks (Imaks), er det særlig fire hensyn som skal ivaretas:
- passasjerenes komfort
- sikkerhet mot sideforskyvning av sporet
- sikkerhet mot avsporing
- sikkerhet mot velting
En tommelfingerregel er at så lenge passasjerkomforten er ivaretatt, er de tre sikkerhetshensynene også godt innenfor kravet. En cirka tallfesting av sikkerhetskravene kan gis utfra verdier for manglende overhøyde (dette er gamle og sannsynligvis noe utdaterte verdier):
- sideforskyvning: I > 200 mm
- avsporing: I > 300 mm
- velting: I > 400 mm
De fleste forvaltninger har grenseverdier for I på mellom 100 mm og 200 mm, avhengig av faktorer som materielltype, sporstandard, kurveradius med mer (se eksempel nedenfor). Når sideforskyvning, avsporing og velting likevel skjer, skyldes dettes om regel at I/ju har vært altfor høy i et kort tidsintervall: I virkeligheten danner ingen kurver perfekte sirkelsegmenter og sporfeil og feil på materiellet gir dynamiske virkninger som kommer i tillegg til de beregnede kreftene. I denne sammenheng har faste punkter i sporet (f.eks sporveksler, broer uten ballast, planoverganger) samme virkning som sporfeil.
| Banedanmark | |
|---|---|
| Maksimal manglende overhøyde I 1) | Maksimal overhøyde h |
|
h = 160 mm |
| Trafikverket, Sverige | |
| Maksimal manglende overhøyde I 2) | Maksimal overhøyde h |
|
h = 160 mm |
| Bane NOR, Norge | |
| Maksimal manglende overhøyde I 3) | Maksimal overhøyde h |
|
h = 150 mm |
- Ved aksellast ≤ 22,5 tonn og 60-kilos skinner
- For hastigheter ≤ 250 km/h. Togkategoriene er satt utfra hvilken manglende overhøyde togene er godkjent for og kategori S skal i tillegg ha krengemekanisme.
- Konvensjonelt materiell er hovedsaklig godstog og plussmateriell hovedsaklig persontog.
(Alle verdier per februar 2014.)
I avsnittet om rullvinkel forklares det hvordan fjæringen av materiellet i en sving reduserer effekten av overhøyden. Grenseverdien for komfort må derfor også ta hensyn til ulike typer materiell i tillegg til spor og sporstandard. Komfortbegrepet blir forøvrig nøye gjennomgått i kapitlet Krengetogstilpasning utfra komfort, men det kan nevnes at grenseverdiene som er diskutert her må variere med hvorvidt en passasjer sitter, står eller går i vogna.
Det må også fastsettes noen grenseverdier for overhøyden, h:
- en absolutt maksimalverdi, hmaks. I Norge er hmaks = 180 mm (for nye persontrafikkbaner, for øvrige baner er hmaks = 150 mm). Høyere verdi tillater større hastighet for de raskeste tog, men er uheldig for saktegående godstog og for steder hvor toget kan komme til å stoppe.
- en maksimalverdi som er avhengig av kurveradius på grunn av avsporingsfaren ved lav hastighet i krappe kurver. For eksempel anbefaler standarden EN 13803 å begrense overhøyden for kurver med radius mindre enn 320 m til
- [math]h_\text{avsp} = \tfrac{R-50}{1,5}[/math] [mm] (der radius er gitt i m) ; (18)
- en maksimalverdi som er avhengig av overgangskurvens lengde og hastighet, utfra hvilken rampestigningshastighet som tillates, se avsnittet om overgangskurver.
- en minimumsverdi utfra hastighet til raskeste tog, finnes ved å snu ligning 5:
- [math]h_\text{min} = \frac{s}{g}\left(\frac{(v_\text{maks})^2}{R}-j_\text{u,maks}\right)[/math] (19)
- en maksimumsverdi utfra hastighet til raskeste tog; det er aldri noe poeng å ha større overhøyde enn den overhøyden som gir likevektshastighet for raskeste tog:
- [math]h_{maks} \leq h_{teor} = \frac{s \cdot (v_\text{maks})^2}{gR}[/math] (20)
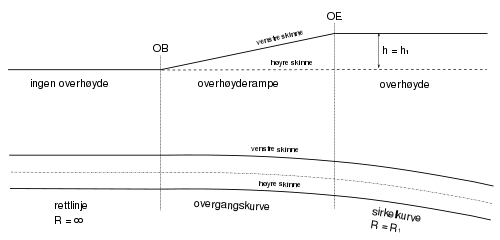
2.4 Overgangskurver og overhøyderamper
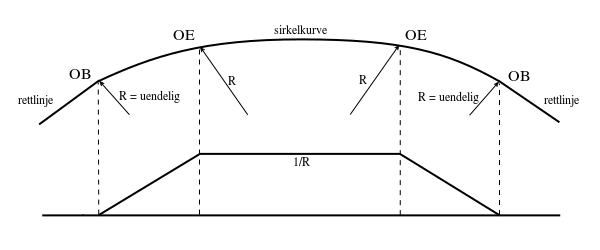
En overgangskurve er definert ved at den har krumning lik tilstøtende kurver i endene og samtidig har kontinuerlig endring av krumning gjennom hele kurven. Overgangskurver benyttes mellom rettlinjer og sirkelkurver og mellom sirkelkurver med ulik radius. Summert er en overgangskurve et traséelement som forbinder to traséelementer med ulik radius. Hensikten er å gi en smidig overgang fra en akselerert tilstand til en annen, med henblikk først og fremst på passasjerkomfort, men også sikkerhet og slitasje på spor og materiell.
For å oppnå overhøyde på sporet anvendes såkalte overhøyderamper, hvor overhøyden bygges opp kontinuerlig. Vanligvis er overhøyderampene sammenfallende med overgangskurvene. Ved kjøring gjennom en overhøyderampe, vil en vogn blir liggende skjevt på sporet. Forenklet kan vi si at dersom vogna var konstruert helt stiv, ville kun tre av fire hjul være på sporet samtidig. Rampen må derfor ikke være brattere enn at alle hjul har sikker føring gjennom hele overhøyderampen/overgangskurven.
Ordforklaringer:
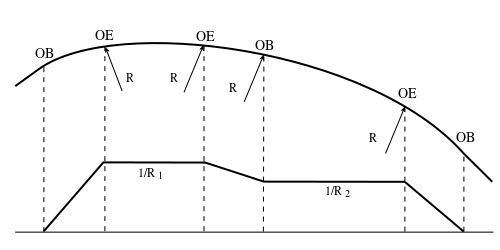
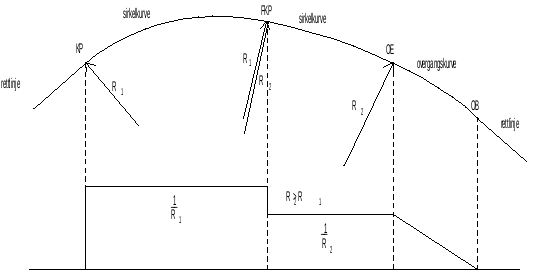
- OB - overgangskurvens begynnelse; punktet i overgangen fra rettlinje til overgangskurve
- OE - overgangskurvens ende; punktet i overgangen mellom overgangskurve og sirkelkurve
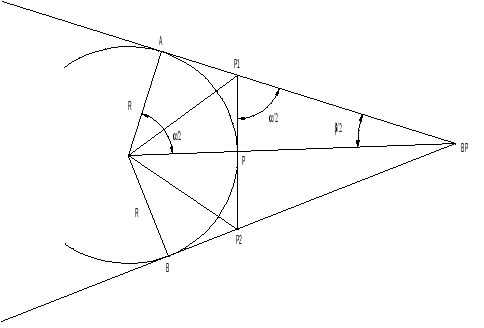
For overgangskurven fra en sirkelkurve til en annen angir betegnelsene OB og OE kurvens tilstøtende punkter mot henholdsvis den slakeste og den krappeste av sirklene.
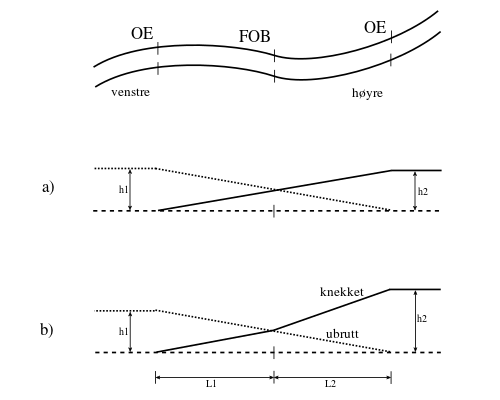
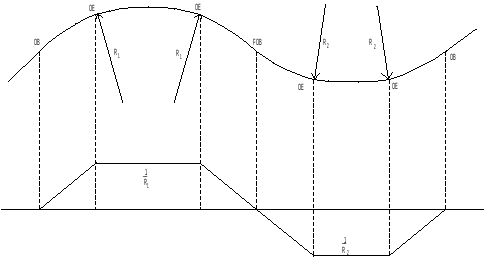
- FOB - felles OB; brukes der det er kontrakurver og ingen rettlinje mellom overgangskurvene
Figur 5 viser det vanligste og enkleste tilfellet der overgangskurven ligger mellom en rettlinje og en sirkelkurve. Figur 6 viser to motsatt rettede sirkelkurver uten rettlinje i mellom. Rampene går da rett i hverandre, men vendepunktet (FOB) har alltid overhøyde lik null. Denne rampeutformingen kalles en sakset overhøyderampe. Hvis de to rampene i saksen har lik stigning, blir situasjonen enkel (figur 6a), mens har de ulik stigning, vil minst en av skinnestrengene få en knekk i FOB (figur 6b). Dette løses ved at den ene strengen løftes ubrutt gjennom hele sakserampen fra OE til OE, for så å bestemme FOBs beliggenhet hvor kravet om null overhøyde skal være oppfylt. Den siste strengen løftes til slutt mellom FOB og endepunktene.
Mange steder er overgangskurvene for korte til at store hastighetsøkninger kan tillates. En kunne ideelt sett ønske seg kurvekorrigeringer som omfattet forlengelse av overgangskurvene, men dette blir fort altfor omfattende og vil medføre store kostnader. Den alternative løsningen på problemet blir derfor å beholde lengden til overgangskurven og samtidig senke rampestigningen.
Tidligere ble denne oppgaven i praksis utført ved å strekke overhøyderampen et stykke inn i sirkelkurven. Enden av rampen ble da ikke sammenfallende med OE og ble benevnt RE - rampens ende. Metoden tillates derimot overhodet ikke i dag, i og med at overhøyden først er bygget helt opp et stykke inne i sirkelkurven. Når hastigheten er høy vil dette gi kritiske utslag på komfort såvel som slitasje.
Dagens løsning består i å redusere overhøyden gjennom hele sirkelkurven, i praksis ved å løfte sporets indre streng.
2.4.1 Klotoiden
Utfra definisjonen av en overgangskurve kan denne utformes på ulikt matematisk grunnlag. I Norge benyttes kun kurver der den kontinuerlige variasjonen i overhøyde og krumning foregår lineært. Denne kurven heter klotoide. I vedlegg xx er en kort forklaring av to andre typer overgangskurver.
Definisjon: En klotoide er en kurve der lengden av kurven L er proporsjonal med krummingen 1/R:
| [math]\frac{1}{R} = C \cdot L = \frac{1}{A^2} \cdot L \;\Rightarrow \; RL = A^2[/math] | (21) |
der konstanten C = 1/A2 er proporsjonalitetskonstanten. Konstanten A kalles klotoideparameteren og beskriver klotoiden entydig akkurat som radien beskriver en sirkelkurve entydig. I Norge er det imidlertid vanlig å bruke R og L til å beskrive klotoiden heller enn A.
Alle omskrivinger av 21 vil også gjelde et vilkårlig punkt på kurven, for eksempel når en kjenner r eller l.
Klotoiden har en enkel ligning, men er komplisert å regne på ettersom den ikke er gitt i kartesiske (rettvinklede) koorinater. Vedlegg 6.1 viser hvordan man utvikler klotoiden i kartesiske koordinater. Reslutatet er følgende parametriske framstilling for x og y:
| [math]x = l - \frac{l^5}{5\cdot 2^2 \cdot A^4 \cdot 2!} + \frac{l^9}{9 \cdot 2^4 \cdot A^8 \cdot 4!} - \frac{l^{13}}{13 \cdot 2^6 \cdot A^{12} \cdot 6!}+\dots[/math] | |
| (22) | |
| [math]y = \frac{l^3}{3 \cdot 2 A^2} - \frac{l^7}{7 \cdot 2^3 \cdot A^6 \cdot 3!} + \frac{l^{11}}{11 \cdot 2^5 \cdot A^{10} \cdot 5!} - \frac{l^{15}}{15 \cdot2^7 \cdot A^{14} \cdot 7!} + \dots[/math] |
Hvis vi tilnærmer de uendelige rekkene med kun sitt første ledd, får vi at [math]x = l[/math] og [math]y = \frac{l^3}{3 \cdot 2 A^2}[/math]. Ved å erstatte variabelen [math]l[/math] i y-uttrykket med x-uttrykket (dvs. erstatte l med x) og sette inn for klotoideparameteren A, får vi
| [math]y = \frac{x^3}{3 \cdot 2 A^2} = \frac{x^3}{6\cdot R\cdot L},[/math] | (23) |
som er den vanlige tilnærmingen til klotoiden når denne brukes som overgangskurve. Dette er en kubisk parabel eller en 3.gradsparabel. Tilnærmingen er akseptabel så lenge L er mye mindre enn R, noe som alltid vil være tilfelle ved overgangskurver. (En mer nøyaktig utledning for tilnærming til klotoiden kan finnes i [3] Kolbjørn Heie, side 408-410.)
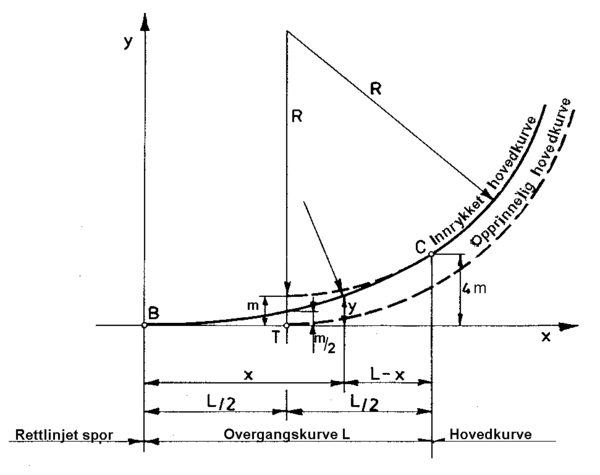
Det er vanlig å betrakte en utgangssituasjon der en ikke har noen overgang mellom rettlinje og sirkelkurve, som illustrert i fig. 7. Rettlinjen ligger på x-aksen og i punktet "T" starter sirkelkurven. Fortsettelsen av x-aksen etter at "sporet" har svingt av kalles tangenten fordi det er tangent til kurvens startpunkt. Origo ligger der vi vil starte overgangskurven (OB, i fig. 7 står det bare "B"). Man kan se fra figuren at 3.gradsparabelen (som starter i "B") gjør at sirkelkurven blir liggende innenfor den opprinnelige sirkelkurven. Avstanden er gitt ved
| [math]m = \frac{l^2}{24R}[/math] | (24) |
Avstanden m kalles ofte "innflyttningen" fordi det er denne avstanden kurven må flyttes innover for å legge inn overgangskurver i en kurve som ikke hadde det fra før. Siden overgangskurven har lineær endring av av radius, vil innflyttningen etter halve lengden L være halvparten av m.
Tabell 4 viser avvik mellom klotoiden og 3.gradsparabelen for ulike overgangskurvelengder og sirkelradier. Lengden L er buelengden til klotoiden, og tallene i tabellen er differansen mellom y-koordinaten til klotoiden, ykloto, og y-koordinaten til 3.gradsparabelen innsatt xkloto i 33:
| [math]y_\text{parab} = \frac{x^3}{6Rl} = \frac{l^3}{6Rl} = \frac{l^2}{6R} = \frac{x_\text{kloto}^2}{6R}[/math] | (25) |
Tabell 2.4Avvik i mm mellom y-koordinat for klotoide og 3.gradsparabel.
| Radius R | |||||
|---|---|---|---|---|---|
| Lengde L | 250 | 300 | 500 | 800 | 1100 |
| 30 | 0,3 | 0,2 | 0,0 | 0,0 | 0,0 |
| 50 | 2,1 | 1,2 | 0,3 | 0,1 | 0,0 |
| 70 | 8,2 | 4,8 | 1,0 | 0,3 | 0,1 |
| 80 | 14,0 | 8,1 | 1,8 | 0,4 | 0,2 |
| 90 | 22,4 | 13,0 | 2,8 | 0,7 | 0,3 |
| 100 | 34,1 | 19.8 | 4,3 | 1,0 | 0,4 |
| 110 | - | 28,9 | 6,3 | 1,5 | 0,6 |
| 120 | - | 40,9 | 8,9 | 2,2 | 0,8 |
I dag brukes klotiden ved prosjektering fordi kravet til nøyaktighet er stort og dataverktøyene er gode. Tidligere ble imidlertid 3.gradsparabelen brukt og mange kurver ute i sporet er opprinnelig utfestet som 3.gradskurver. Praktiske oppgaver på sporet, som justering, etter klotoidebaserte data, kan dermed skape konflikter, ettersom klotoiden alltid krummer noe mer enn 3.gradsparabelen.
For mer informasjon om klotoiden, se:
2.4.2 Traseringsparametre i overgangskurven
Rampestigning er den ene skinnens stigning i forhold til den andre skinnen og er gitt ved følgende uttrykk, som vanligvis oppgis i promille:
| [math]p = \frac{\Delta h}{\Delta L}\text{ eller }p = \frac{dh}{dl},[/math] | (26) |
der Δh er forskjellen i overhøyde over lengden ΔL. Det første uttrykket (med delta) er tilstrekkelig for bruk i Norge, hvor rampene har lineær stigning. Hvis vi ser bort fra eventuelle sporfeil, så skal rampestigningen gjennom hele rampen være p = h/L (for overgangskurve mellom rettlinje og sirkelkurve). Diffrensialformen må brukes for ramper som ikke er lineære (ulik stigning avhengig av hvor i rampen man befinner seg).
I en overhøyderampe vil overhøyden variere fra punkt til punkt, den bygges opp fra ingen overhøyde der den er tilknyttet rettlinje og til full overhøyde der sirkelkurven begynner.
På grunn av de skjevheter en overhøyderampe innebærer, kalles rampestigningen også for vindskjevhet. Men dette begrepet er mer forbundet med sporfeil. Vi kan si at rampestigning er den tilsiktede endringen av overhøyde i lengderetningen, mens vindskjevhet er den faktiske situasjonen på sporet (tilsiktet skjevhet pluss eventuelle feil).
Hvis en helt stiv vogn uten fjærer hadde kjørt over en overhøyderampe, ville skjevheten i rampen ført til at vognen hadde kun to hjul på sporet, den ville stått og vippet. I virkeligheten er selvsagt vognene ikke helt stive og de har i tillegg fjæring, men overhøyderampene fører likevel til en avlastning av noen av hjulene: Vertikalkraften mellom hjul og skinne vil bli ulik for hvert av hjulene idet vogna kjører over overhøyderampen. Samtidig virker en føringskraft (horisontalkraft) på hjulene fordi man kjører i en kurve. Dersom føringskrafta blir tilstrekkelig stor og vertikalkrafta tilstrekkelig liten, sporer vogna av. Forholdet mellom føringskraft og vertikalkraft kalles Y/Q-forholdet og blir nærmere omtalt i Teknisk linjeføring: Avsporingsfare.
I Norge, som i de fleste europeiske land er maksimal rampestigning satt til 1:400, dvs 2,5 promille.
Rampestigningshastighet er overhøydens endring per tidsenhet og er gitt ved:
| [math]\frac{\Delta h}{\Delta t}\text{ eller }\frac{dh}{dt},[/math] | (27) |
med enhet mm/s.
For rette ramper, som er det som brukes i Norge, kan rampestigningshastigheten skrives som:
| [math]\frac{dh}{dt} = \frac{h}{L/v} = v\cdot \frac{h}{L},[/math] | (28) |
der L er lengden av overhøyderampen (her antar vi dessuten av hastigheten er konstant gjennom hele rampen).
Rampestigningshastighet kan også oppgis som et stigningsforhold 1:n*V der n er et heltall og V er hastighet i km/h, men denne skrivemåten er ikke så vanlig nå lenger. For å finne rampestigningshastigheten i mm/s utfra stigningsforholdet: dh/dt = 1000/(n*3,6) [mm/s].
Størrelsen på rampestigningshastighet er først og fremst viktig for passasjerenes komfort. Ved gjennomkjøring av en overhøyderampe vris vognkassen om sin lengdeakse. Særlig passasjerer som står eller går kan oppleve dette som ubehagelig, mens sittende passasjerer ikke merker så mye til enkeltkurver. På kurverike baner kan enkelte passasjerer (også de som sitter) bli kvalme (sjøsyke/"togsyke") på grunn av de gjentatte bølgelignende bevegelsene i toget. Særlig i krengetog har togsyke vært et problem, ettersom krengingen gjør at den opptredende rampestigningen i toget blir større samtidig som at krengetogene ofte kjører fortere enn andre passasjertog.
En beslektet størrelse er rullvinkelhastigheten eller vridningshastigheten som angir hvor mye tverrvinkelen endrer seg per tidsenhet, altså hvor fort vognkassen vrir seg. Sammenhengen mellom rullvinkelhastigheten β og rampestigningshastigheten dh/dt er (for små vinkler) gitt ved
| [math]\beta = \frac{dh/dt}{s},[/math] | (29) |
der s er sporvidden i mm og β er gitt i radianer per sekund. For å få resultatet i grader per sekund ganges det med 180/pi.
Rykk er endring av ukompensert sideakselerasjon per tidsenhet, det vil si den deriverte av ju. Dette er som nevnt et uttrykk for hvor fort den ukompenserte sideakselerasjonen endres over tid:
| [math]\psi = \frac{\Delta j_x}{\Delta t}\text{ eller }\psi = \frac{dj_x}{dt}[/math] | (30) |
der jx er den ukompenserte sideakselerasjonen etter lengden x. Ukompensert sideakselerasjon blir vanligvis betegnet ju, men da er det snakk om den maksimale som opptrer i kurvens endepunkt (OE). jx er gitt ved [math]j_x = \frac{x}{L}\cdot j_u[/math].
Dersom overgangskurven har lineær endring av radius (slik som klotoiden) og hastigheten er konstant gjennom kurven, kan rykket skrives slik:
| [math]\psi = \frac{dj_u}{dt} = v\cdot \frac{dj_x}{dx} = v\cdot \frac{j_u}{L}[/math] | (31) |
Siden ukompensert sideakselerasjon også kan uttrykkes som manglende overhøyde, er rykket også definert som endring av den manglende overhøyden:
| [math]\frac{dI}{dt} = \frac{s}{g} \cdot \psi = \frac{v \cdot s}{g} \cdot \frac{dj_x}{dx}[/math] | (32) |
der det siste uttrykket fremkommer ved å sette inn (31) for ψ og gjelder under samme betingelser som formel 31.
2.4.3 Overgangskurvens lengde og hastighet i overgangskurven
Overgangskurvens lengde bestemmes ut fra de tre traseringsparametrene rampestigning, rampestigningshastighet og rykk. Ved å løse de tre ligningene (26), (28) og (31) for L, får vi
[math]L_1 = \frac{h}{p}, \,\,\,\, L_2 = v\cdot \frac{h}{(\tfrac{dh}{dt})}, \,\,\,\, L_3 = v\cdot \frac{j_u}{\psi},[/math]
der v er hastighet i meter per sekund.
Setter inn maksimalverdier for traseringsparametrene:
| [math]L_1 \leq \frac{h}{p_\text{maks}}[/math] | (33) |
| [math]L_2 \leq v\cdot \frac{h}{(\tfrac{dh}{dt})_\text{maks}}[/math] | (34) |
| [math]L_3 \leq v\cdot \frac{j_u}{\psi_\text{maks}}[/math] | (35) |
Minste lengde på overgangskurven med den gitte hastigheten er da Lmin = max{L1, L2, L3}.
[math]L_1 \leq \frac{h}{p_\text{maks}} = \frac{120}{2,5} = 48[/math]
[math]L_2 \leq v\cdot \frac{h}{(\tfrac{dh}{dt})_\text{maks}} = 25 \cdot \frac{120}{55} \approx 54,5[/math]
[math]L_3 \leq v\cdot \frac{j_u}{\psi_\text{maks}} = 25 \cdot \frac{0,47}{0,52} = 22,6,[/math]
der ju er regnet ut slik (lign. 4):
[math]j_u = \frac{v^2}{R} - g\cdot\frac{h}{s} = \frac{25^2}{500} - 9,81\cdot\frac{120}{1500} \approx 0,47[/math]
Overgangskurven(e) må dermed være minst 55 meter (runder opp til nærmeste hele meter).
(Kan også i første omgang sette inn maksimalverdi istedenfor opptredende verdi av ju i L3, men dersom L3 da blir utslagsgivende bør man regne ut ju slik det er gjort ovenfor.)
Dersom målet er å finne maksimal hastighet over kurvekombinasjonen, er det vanlig å først regne ut maksimal hastighet i sirkelkurven for så å finne ut om overgangskurvelengdene tillater denne hastigheten.
For sirkelkurven blir maksimalhastighet
[math]v_\text{maks} = \sqrt{500 \left(\frac{9,81 \cdot 120}{1500}+0,85\right)} \approx 28,6 \;\text{m/s}.[/math]
Setter så denne hastigheten inn i beregningene for lengde av overgangskurven:
[math]L_1 \leq \frac{h}{p_\text{maks}} = \frac{120}{2,5} = 48[/math]
[math]L_2 \leq v\cdot \frac{h}{(\tfrac{dh}{dt})_\text{maks}} = 28,6 \cdot \frac{120}{55} \approx 62,4[/math]
[math]L_3 \leq v\cdot \frac{j_u}{\psi_\text{maks}} = 28,6 \cdot \frac{0,85}{0,52} = 46,8,[/math]
der ju er regnet ut på samme måte som ovenfor (her havner ju nødvendigvis på maksimalverdien siden hastigheten er den høyeste som er tillatt i sirkelkurven).
Dersom overgangskurvene er minst 63 meter lange kan hastigheten settes til 28,6 m/s (tilsvarer 103 km/h).
En annen mulighet er å beregne maksimalhastighet utfra formlene for rampestigningshastighet og rykk hver for seg. For førstnevnte er det enkelt idet vi løser ligning (28) med hensyn på hastighet der maksimalverdi for rampestigningshastiget er satt inn:
| [math]v_\text{maks} = \frac{L}{h}\cdot (\dfrac{dh}{dt})_\text{maks}[/math] | (36) |
For rykket gjøres akkurat det samme med ligning (31):
[math]v_\text{maks} = \frac{L}{j_u} \cdot \psi_\text{maks}[/math]
Problemet er bare at ju er avhengig av hastigheten. Ved å sette inn for ju får vi følgende tredjegradsuttrykk
[math]v_\text{maks} = \frac{L}{\frac{v_\text{maks}^2}{R}-\frac{g\cdot h}{s}} \cdot \psi_\text{maks}[/math]
Hvis uttrykket omformuleres til
| [math]v_{n+1} = \sqrt{R\cdot \left(\frac{L\cdot \psi_\text{maks}}{v_n} + \frac{g\cdot h}{s} \right) }[/math] | (37) |
kan man iterere seg fram til løsningen.
2.5 Kurvekombinasjoner
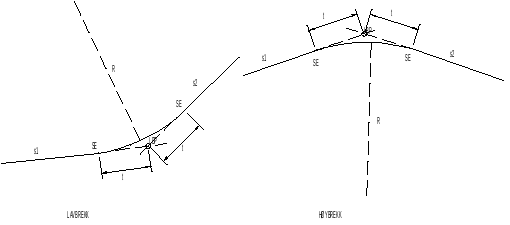
Dette avsnittet beskriver hvordan de tre traseringselementene rettlinje, sirkelkurve og overgangskurve kan kombineres ute i sporet. Det enkleste kurveforløpet vi har består av overgangen fra rettlinje til sirkelkurve og tilbake igjen via overgangskurver, se figur 8. Denne kalles en enkel kurvekombinasjon.
Kombinasjonskurver er flere tilstøtende, ensrettede sirkelkurver med ulik radius, se figur 9. Her gjelder de samme traseringskrav som for enkle kurver, men formlene blir litt mer kompliserte, se eksempel.
En annen vanlig kurvesammensetning er motsatt rettede kurver, eller kontrakurver, som betyr tilstøtende kurver med krumning med ulikt fortegn, se figur 12. Overgangskurvene får OB i samme punkt, som da kalles felles OB; FOB.
Ved nyprosjektering vil man helst unngå både kombinasjonskurver og kontrakurver der det er mulig. Dersom man kan legge en rettlinje imellom og få to enkle kurvekombinasjoner er det som regel en bedre løsning. Rettlinjen må imidlertid ha en viss lengde for at det ikke skal bli ukomfortabelt å kjøre over; generelt bør alle traseringselementene ikke være særlig kortere enn at det tar minst 0,9 sekunder å kjøre gjennom hvert av dem.
2.5.1 Kurver uten overgangskurver
Dersom kurveradius er stor eller hastigheten er liten, kan overgangskurver utelates. Dette gjøres av konstruktive årsaker, og særlig på stasjoner i kontrakurver og i sporveksler. Punkter der rettlinje går direkte over i sirkelkurve betegnes kurvepunkt KP, mens punkter med en momentan overgang fra en sirkelkradius til en annen betegnes felles kurvepunkt FKP.
For sirkelkurver uten overhøyde er som regel også overgangskurver utelatt. Endring i krumning og dermed sideakselerasjon skjer i dette tilfellet momentant. Rykket blir her svært stort. Allikevel skjer det en utjevning i praksis, siden materiellet som trafikkerer linjen ikke er stivt, men utstyrt med fjæringsmekanismer. Fig. 11 illustrerer hvordan vognas faktiske akselerasjon arter seg ved inn- og utgang av en sirkelkurve med rettlinjer i endene.
De ulike forvaltningene har fastsatt grenser for i hvilken utstrekning kurver uten overgangskurver kan benyttes, men innfallsvinkelen varierer. Én måte er å angi at endring til en manglende overhøyde I ikke skal overstige en viss verdi, f.eks 100 mm. En annen metode er å operere med en såkalt fiktiv overgangskurve. Som overgangskurve brukes da avstanden mellom vognens boggiesentre (ofte ca 2 meter). Denne kan så settes inn i de vanlige formlene sammen med en akseptabel verdi for den ukompenserte sideakselerasjonen for å finne et utrykk for hvilken hastighet en kan benytte til hvilken kurveradius.
Det er enklest å bruke den første metoden. Vi finner verdien av den ukompenserte sideaksellerasjonen i punktet FKP (eller KP),
[math]j_u = \frac{v^2}{R}[/math] for enkel kurve (rettlinje-sirkelkurve),
[math]j_u = \frac{v^2}{R_2} - \frac{v^2}{R_1}[/math] for kombinasjonskurver (ensrettede kurver) der R1 > R2
og
[math]j_u = \frac{v^2}{R_1} + \frac{v^2}{R_2}[/math] for kontrakurver.
Ved å sette en maksimalverdi for brå endringer av ju kan vi løse ligningene ovenfor og finne maksimal tillatt hastighet over hver FKP. Tillatt verdi for denne plutselige endringen av ju er vanligvis lavere enn de andre grenseverdiene, f.eks kan den ligge på rundt 0,65 m/s3 (tilsvarer I = 100 mm).
2.5.2 Bufferoverdekning i kontrakurve
Når man kjører gjennom en kontrakurve, vil vognenes buffere (hvis vognen har dette) bevege seg sideveis i forhold til hverandre. Hvis denne bevegelsen blir for stor, er det fare for at buffrene hekter seg i hverandre og vognene vil dra hverandre av sporet. Dette kalles ombufring og skjer kun ved små radier i kontrakurver. Ved å legge inn større radier og/eller rettlinje mellom kurvene, sikrer man ønsket bufferoverdekning. Samtidig blir rykket mindre, noe som er fordelaktig for komforten. Ombufring er kun et problem når radiene i kontrakurven er mindre enn ca. 250 meter.
3 VERTIKALKURVATUR
3.1 Kurver i vertikalplanet
Geometrien for vertikalkurvaturen er langt enklere enn den for horisontalkurvaturen. Isolert sett består den vertikale traséen av kun to traseringselementer: Stigninger (rettlinjer) og stigningskurver (sirkelkurver) i vertikalplanet. Tilsammen utgjør disse kurvene vertikalkurvaturen.
Linjens vertikalføring fremgår av lengdeprofilet for en gitt banestrekning, som angir størrelsen på stigning og fall på de forskjellige stedene på linjen. Stigning og fall angis i promille.
Tabell 5 angir fordelingen av stigning/fall i vertikalplanet for ulike eksisterende baner i Norge, der stigningene gjelder for alle rettlinjene i vertikalkurvaturen:
| > 25 ‰ | 20,1-25 ‰ | 15,1-20 ‰ | 10,1-15 ‰ | 5,1-10 ‰ | 0,1-5 ‰ | horisontalt | Største stigning | |
|---|---|---|---|---|---|---|---|---|
| Østfoldbanen, vestre linje | 0 % | 2 % | 0 % | 25 % | 35 % | 27 % | 11 % | 25 ‰ |
| Østfoldbanen, østre linje | 0 % | 0 % | 0 % | 41 % | 33 % | 18 % | 8 % | 13 ‰ |
| Dovrebanen | 0 % | 0 % | 16 % | 18 % | 16 % | 31 % | 19 % | 18 ‰ |
| Kongsvingerbanen | 0 % | 0 % | 0 % | 0 % | 5 % | 75 % | 19 % | 5 ‰ |
| Rørosbanen | 0 % | 0 % | 0 % | 14 % | 30 % | 37 % | 19 % | 15 ‰ |
| Nordlandsbanen | 0 % | 0 % | 13 % | 14 % | 24 % | 25 % | 25 % | 19 ‰ |
| Gjøvikbanen | 1 % | 4 % | 40 % | 32 % | 10 % | 7 % | 7 % | 22 ‰ |
| Bergensbanen | 0 % | 9 % | 18 % | 14 % | 18 % | 33 % | 8 % | 21 ‰ |
| Sørlandsbanen | 0 % | 7 % | 17 % | 18 % | 20 % | 20 % | 17 % | 25 ‰ |
| Vestfoldbanen | 0 % | 0 % | 7 % | 27 % | 33 % | 21 % | 11 % | 14 ‰ |
| Solørbanen | 0 % | 0 % | 0 % | 0 % | 20 % | 53 % | 28 % | 8 ‰ |
| Roa - Hønefoss | 0 % | 5 % | 69 % | 18 % | 2 % | 3 % | 3 % | 20 ‰ |
| Raumabanen | 0 % | 1 % | 23 % | 10 % | 16 % | 27 % | 24 % | 20 ‰ |
| Hell - Storlien | 0 % | 0 % | 32 % | 8 % | 16 % | 26 % | 18 % | 19 ‰ |
| Grong - Namsos | 0 % | 0 % | 0 % | 8 % | 33 % | 16 % | 43 % | 11 ‰ |
| Randsfjordbanen | 0 % | 0 % | 0 % | 13 % | 42 % | 32 % | 13 % | 11 ‰ |
| Flåmsbanen | 83 % | 0 % | 0 % | 0 % | 4 % | 9 % | 3 % | 55 ‰ |
| Asker - Spikkestad | 0 % | 0 % | 0 % | 10 % | 31 % | 37 % | 23 % | 11 ‰ |
| Arendalslinjen | 0 % | 0 % | 4 % | 24 % | 9 % | 23 % | 39 % | 22 ‰ |
| Ofotbanen | 0 % | 1 % | 26 % | 58 % | 3 % | 6 % | 6 % | 17 ‰ |
| Øvrige baner | 0 % | 1 % | 17 % | 22 % | 36 % | 18 % | 5 % | - |
| Totalt | 1 % | 2 % | 13 % | 17 % | 22 % | 28 % | 18 % | 55 ‰ |
3.2 Stigninger
Med stigning menes her en rettlinje i vertikalplanet som avviker i retning fra en horisontal referanseflate. Kjøreretningen bestemmer om stigningen har positivt (reell stigning) eller negativt (fall) fortegn.
3.2.1 Stigning og motstand
De viktigste avveiningene for å optimalisere stigning og fall er anleggsomkostningene, som kan begrenses ved større stigninger (kortere kjørevei), og driftskostnadene, som raskt vokser ettersom behovet for kraftigere trekkraft gjør seg gjeldende. Likeledes kreves bremsekraft ved fall.
Alt rullende materiell må overvinne en kjøremotstand under fremføringen. Denne består hovedsaklig av tre ledd: Grunnmotstanden, som utgjøres av friksjon etc., kurvemotstanden i horisontalkurver, og stigningsmotstanden. I vertikalgeometrien fokuserer vi på sistnevnte og dens samspill med den totale kjøremotstanden. Fenomenet består av tyngdekraftens komponent parallelt sporets lengderetning og er helt analogt med tyngdens komponent på tvers av kjøreretningen i kurver med overhøyde. Grundigere beskrivelse av kjøremotstand finnes i Teknisk linjeføring: Kjøremotstand.
Som regel er ikke stigningen større enn at vi kan tilnærme stigningen (lik tangens til v) med vinkelen v selv.
En uskadelig stigning er en stigning som innebærer mindre motstand enn grunnmotstanden og som derfor ikke gir større trafikkostnader enn på en flat strekning. I motsatt fall har vi en skadelig stigning.
På en del av våre eldre eksisterende baner, vil vertikalkurvaturen vise tegn på tidligere begrensninger hos det rullende materiell. Materiellet hadde ofte ikke kraft nok til å forsere en ideell stigning, dvs. helt jevn stigning fra et punkt til et annet, men måtte ha gjentatte intervaller av varierende stigning, og til og med fall, når den totale kjøremotstanden ble for høy. Disse intervallene fremkom ved å redusere stigningen med kurvemotstanden, slik at lengdeprofilet ble brukket i de horisontale kurvepunktene. Uskadelig stigning er/var sjelden mulig å få til, men en hovedutfordring bestod i å unngå såkalt tapt stigning, dvs. at avvikene fra jevn stigning medførte økt energiforbruk.
3.2.2 Bestemmende fall og stigning
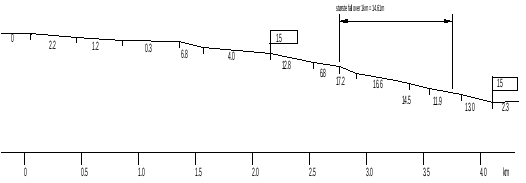
Bestemmende fall er det fall i promille som beregnes ved å forbinde to punkter i strekningens lengdeprofil med innbyrdes avstand lik 1000 m med en rett linje (tilsvarende for bestemmende stigning). For en lengre strekning er det bestemmende fall/stigning den største verdien som fremkommer på en vilkårlig kilometer langs strekningen med denne beregningen.
I fig. 14 er det bestemmende fall fra km 0 til km 2.1 mindre enn 5 ‰ (dette er såpass lite at det ikke skiltes). Fra km 2.1 til km 4.1 er det bestemmende fall lik 14.6 ‰ og anvises derfor avrundet til 15. Største fall er 17.2 ‰.
Bestemmende fall/stigning vil naturlig nok stille ulike krav til ulik trafikk og materiell. Derfor har alle forvaltninger strenge krav til største bestemmende fall/stigning. Vanlig krav er 12,5 ‰ ved nybygging (med muligheter for unntak). Som man ser av tabell 5 har vi i Norge mange steder større stigninger på deler av nettet.
I enkelte tilfeller kan sporets absolutte fall/stigning angis i stedet for det bestemmende. Dette gjelder når det forekommer store fall/stigninger over en kort strekning på stasjoner eller sidespor, hvor det f.eks. foregår skifting.
Prosjektering av vertikalkurvaturen er i stor grad avhengig av hastigheten til det materiellet som skal trafikkere den aktuelle strekningen. Største tillatte kjørehastighet for tog på strekninger med fall er ikke bare avhengig av den oppsatte hastigheten i sporavsnittet, men også av togets bremseutstyr og det bestemmende fall på strekningen.
Når en ny linje driftsmessig er å betrakte som en forlengelse av en eksisterende bane, eller når det gjelder linjeomlegging, er det uansett en fordel om bestemmende fall ikke overstiger det som gjelder for den eksisterende banen. Dette for ikke å skape nye flaskehalser for tunge godstog.
Der hvor materiell hensettes (stasjoner, sidespor, oppstillingsspor) bør sporet helst anlegges horisontalt eller med mindre stigning/fall enn grunnmotstanden (som kan regnes i promille, se Teknisk linjeføring: Grunnmotstand). Dette er et sikkerhetshensyn for å hindre at materiell som står stille begynner å rulle.
3.3 Stigningskurven
I forrige avsnitt ble det vist et lengdeprofil fra vertikalkurvaturen, der stigning og fall endres i brukne rettlinjer. Men for å få jevn vertikalkurvatur, må hvert slikt brytningspunkt, eller brekkpunkt, rundes av med en sirkelkurve i vertikalplanet, en såkalt stigningskurve eller vertikalkurve.
Stigningskurven fungerer som overgang mellom de ulike stigninger. I teoretisk prosjekteringssammenheng benyttes imidlertid ikke stigningskurver der stigningsforskjellen ikke overstiger 1 ‰.
Figur .15 viser utgangspunktet for innlegging av en stigningskurve. Brytningspunktet (BP) angir hvor kurven skal ligge - enten over eller under knekken i det eksisterende terrenget. Nødvendig utstrekning angis ved stigningskurvens ender (SE). Ved overgang til større stigning, eller til lavere fall, har vi såkalt lavbrekk. I motsatt fall har vi høybrekk.
3.3.1 Radius
Vertikalkurvens radius fastsettes normalt ved å ta hensyn til reduksjon av aksellasten i vertikalkurver i høybrekk, eller konvekse kurver, som vist i fig. .15. Videre må det tas hensyn til klaringen mellom spor og rullende materiell, som blir dimensjonerende størrelse for spor som trafikkeres med lave hastigheter. Komfort er sjelden dimensjonerende faktor for å bestemme vertikalradius.
Tidligere ble vertikalkurvens radius regnet ut som kvadratet av hastigheten i km/h. Med dagens hastigheter gir det altfor store radier som er vanskelige å tilpasse horisontalgeometrien. Eksempelet nedenfor viser henholdsvis normalkravet og minstekravet til radius i vertikalkurver. Det er en fordel å benytte større radier der det er mulig.
| Normale krav | Minste krav |
|---|---|
| Rv = V2/2,6 [m] Minste Rv = 4000 m |
Rv = V2/3,9 [m] Minste Rv = 2500 m |
(V er gitt i km/h)
Dersom vertikalkurver faller sammen med kurver i horisontalplanet, vil sporets geometri bli komplisert, og overhøyde- og vindskjevhetsfeil kan oppstå. Derfor bør stigningskurvene så langt det er mulig ligge i horisontale rettlinjer og ikke sammenfalle med overgangskurver eller sporveksler. Sammenfall med sirkelkurver i horisontalplanet er ikke like problematisk.
3.3.2 Lengde på kurven
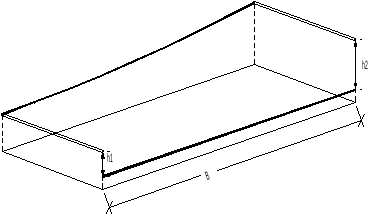
Ser vi igjen på fig. .15 fra avsnitt 3.3, kan vi finne et uttrykk for lengdene t. Vi forutsetter i første omgang at sirkelkurven legges inn slik at disse kan betraktes som tangenter til kurven. Figur .16 illustrerer situasjonen for to vilkårlige kryssende tangenter til en sirkelkurve:
De to tangentene har samme lengde og som uttrykkes ved:
| [math]A,BP = B,BP = R\cdot\tan\frac{\alpha}{2}[/math] | (49) |
Siden stigning og fall utgjør svært små vinkler, kan en tilnærme størrelsene, som egentlig er forholdstall og dermed tangens til vinklene, med vinklene selv. Dermed kan vi skrive:
| [math]A,BP = B,BP \approx R\cdot\frac{\alpha}{2}[/math] | (50) |
Ved å betrakte figur 16 i forhold til horisontalplanet, kan det gjennom en del vinkelbetraktninger vises at vinkelen α/2 er halve forskjellen mellom stigningene. Dermed ender vi opp med et uttrykk for t som funksjon av stigning og kurveradius:
| [math]t = \frac{s_2-s_1}{2} \cdot R[/math] | (51) |
der t er lengden til “tangentene” til de to halvpartene av kurven som utgjør henholdsvis de ulike stigningene s1 og s2, gitt som forholdstall. Her er det viktig å bruke riktig fortegn, slik at fall inngår som “negativ stigning”.
Som for stigninger gjelder det at stigningskurvens lengde ikke skal være kortere enn 20 m.
3.3.3 Heving og senking
I høybrekk foretar vi en senking av brytningspunktet BP ned til punktet P, mens i lavbrekk foretar vi en såkalt heving, jf. figur 15. Betrakter vi figur 16, ønsker vi å finne heving/senking som lengden BP,P. Utfra de påtegnede vinkler fås følgende sammenheng:
| [math]BP,P = P_1,P \cdot \tan\frac{\alpha}{2} = R\cdot \tan\frac{\alpha}{2}\cdot \tan\frac{\alpha}{4}[/math] | (52) |
Igjen kan vi tilnærme tangens til vinkelen med vinkelen selv, som dermed gir:
| [math]m_v = BP,P \approx R\cdot \frac{\alpha}{2}\cdot \frac{\alpha}{4} = R\cdot \frac{\alpha^2}{8} = R\cdot \frac{(s_2-s_1)^2}{8} = \frac{t^2}{2R}[/math] | (53) |
Uttrykket helt til høyre i 53 er det vanlige uttrykket for heving og senking, som funksjon av tangentlenden t og kurveradius.
4 Geometriske feil - vedlikehold
Til nå i dette kapitlet har vi først og fremst konsentrert oss om en rekke teoretiske aspekter ved sporgeometrien, dvs. geometrisk utforming etter ideelle ønsker. Sporet er imidlertid gjenstand for stadige justeringer, og i det følgende skal vi belyse en del geometriske feil som oppstår. Feil i sporet er forøvrig grundigere beskrevet i kapitlene L534 – Sporjustering og L535 – Tilstandskontroll.
For geometriens, eller kurvaturens del, er det særlig fire geometriske feil vi ønsker å minimalisere: Vindskjevheter, avvik i side og høyde og uriktig overhøyde. En skulle umiddelbart regne med at de ulike geometriske feilene hadde samme karakter og utbedring for nær identiske spor- og trafikkforhold, men grundige undersøkelser over tid har ikke kunnet bekrefte dette. Hverken trafikkmengde/-type eller sporkonstruksjon kan på statistisk grunnlag vise til noe entydig forringelse av geometrien eller vedlikeholdsbehov.
Derimot kan det vises at høyde- og sidefeil øker lineært både med aksellast og tiden mellom vedlikehold, utenom den initielle justeringen av sporet.
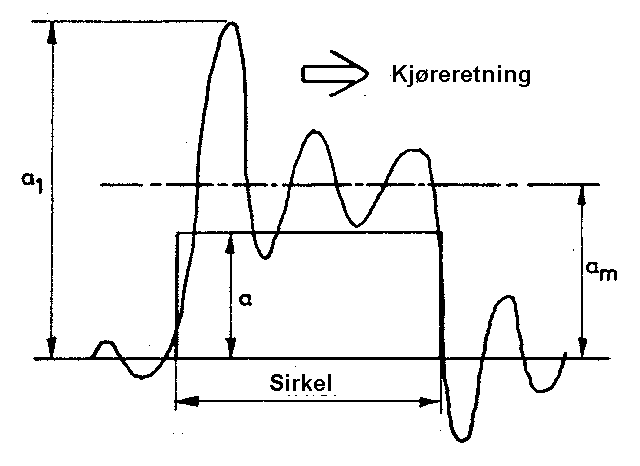
4.1 Vindskjevhet
4.1.1 Definisjon og årsak
Fenomenet forekommer i to former: tilsiktet og utilsiktet vindskjevhet. Den tilsiktede vindskjevheten finnes i overhøyderamper og kalles rampestigning. Utilsiktet vindskjevhet er som regel langt større, og den kan oppstå som en geometrisk feil i spor med telefarlige masser, ustabiliserte spor og etter eller under gravearbeider. Den vanligste definisjonen av vindskjevhet er forskjell i overhøyde, målt over en gitt basis. Dette innebærer at skinnestrengene ikke er parallelle i vertikalplanet, men har ulik stigning. En annen definisjon av vindskjevhet er hvis vi tenker oss en helt stiv vogn med fire hjul: Ved vindskjevt spor vil kun tre av hjulene berøre sporet. Avstanden fra det fjerde og ned på skinnestrengen blir dermed sporets vindskjevhet.
4.1.2 Konsekvens
For å se på følgene av vindskjevt spor, er den stive vogna uten fjæring et godt utgangspunkt. Når denne går inn i en overgangskurve og opp en overhøyderampe fra en rettlinje, vil det fremre, ytre hjulet påvirkes av en økt kraft, mens det bakre, ytre hjulet vil avlastes - i det svært teoretiske tilfellet totalt. Ut av sirkelkurven igjen og ned en overhøyderampe skjer det motsatte - det fremre, ytre hjulet avlastes.
For eksisterende rullende materiell er situasjonen den samme, bare mer komplisert på grunn av materiellets dynamiske egenskaper og avhengig av hvor bratt den aktuelle rampa er. Som oftest finnes lokale, utilsiktede vindskjevheter innenfor rampa, som dermed må legges til den tilsiktede vindskjevheten. Hvis denne summen blir stor nok får det ytre hjulet avlasting nok til å klatre over skinnekanten og vi får avsporing. Det er altså i ramper med minkende overhøyde faren for avsporing er aller størst.
4.2 Side- og høydefeil
4.2.1 Definisjon og årsak
Side- og høydefeil er kort og godt avvik fra horisontal- og vertikalkurvatur og måles i stor grad ved de samme prinsipper. Ved justering av sidebeliggenheten, eller baksing, justeres alltid høydebeliggenheten samtidig.
Vi skiller mellom tre nivåer av feil: farlige, skadelige og uskadelige feil. Førstnevnte er en fare for sikkerheten og må rettes omgående når de oppdages. Skadelige feil rettes så snart som mulig, etter at alle farlige feil for et strekke er rettet. De uskadelige feilene må holdes under observasjon slik at vedlikeholdet er tilstrekkelig til at de ikke utvikler seg til skadelige feil.
4.2.2 Konsekvens
Slike feil forårsaker en slingrende toggang, som igjen vil forårsake ujevn slitasje på skinnene og befestigelsen. Dessuten kan feil i sidebeliggenheten forårsake solslyng på skinnene.
4.3 Overhøydefeil
4.3.1 Årsak
Hvis den tilsiktede overhøyden i en kurve ikke er oppnådd ved en justering, vil belastning av sporet lett kunne påføre kurven ytterligere avvik fra ideell overhøyde. Dermed går vi inn i en ond sirkel hvor feilen bare vokser.
4.3.2 Konsekvens
Dersom følgen av dårlig justering er for stor overhøyde, får vi et større overhøyde overskudd enn vi har regnet med for godstogene. Følgelig kan disse forskyve sporet så hardt innover i kurven at det ødelegger sporet. I motsatt fall blir den manglende overhøyden I så stor for det raskeste materiellet at vi får avsporing.
Brå feil i overhøyden kan også gi feil i baksen. Når disse blir store, oppstår ofte også en sporutvidelse samme sted.
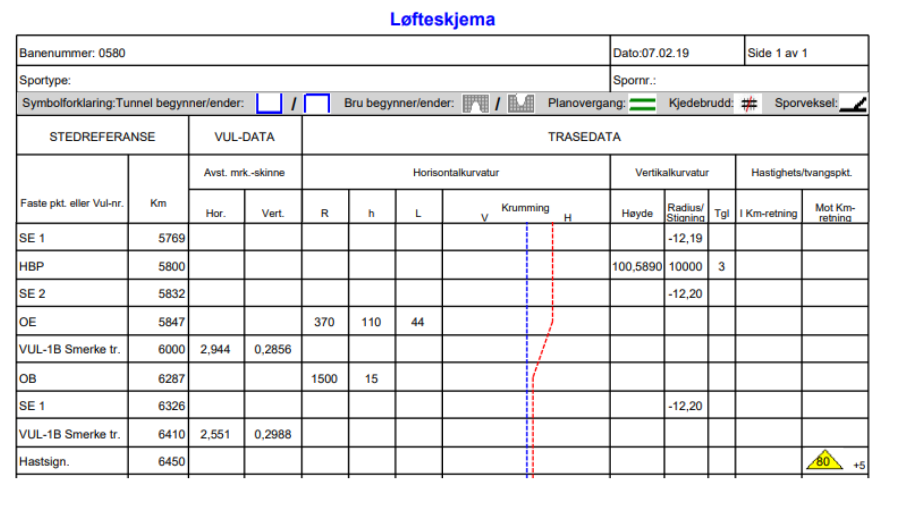
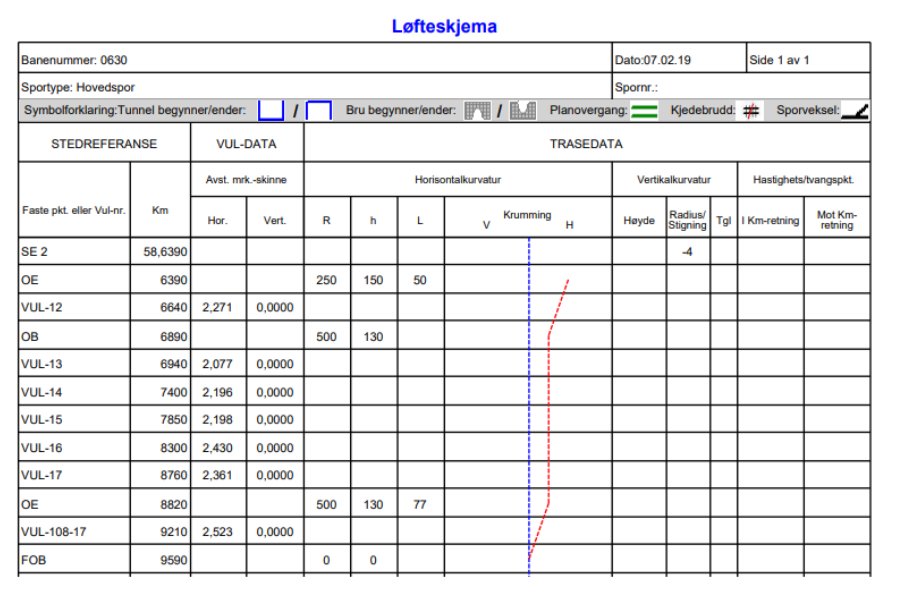
4.4 Registrering av kurvatur - løfteskjema
I avsnitt 2.6 om horisontalkurvatur ble de mest anvendte kurvekombinasjonene vist i figurer. Figurene 8 og 12 viser henholdsvis den alminnelige overgangen mellom rettlinje og sirkelkurve, ved hjelp av overgangskurve, og bruk av tilstøtende overgangskurver for kontrakurver (FOB). Begge typer forekommer både med og uten mellomliggende rettlinje. Disse kurvekombinasjonene kan vi betegne som lovlige kombinasjoner. Direkte overgang fra rettlinje til sirkelkurve skal derimot ikke forekomme på hovedspor. Da har vi i så fall en ulovlig kombinasjon. Det som derimot forekommer en del er såkalte felles kurvepunkt (FKP). Disse utgjør gjerne en liten endring i krumning fra en sirkelkurve til en annen.
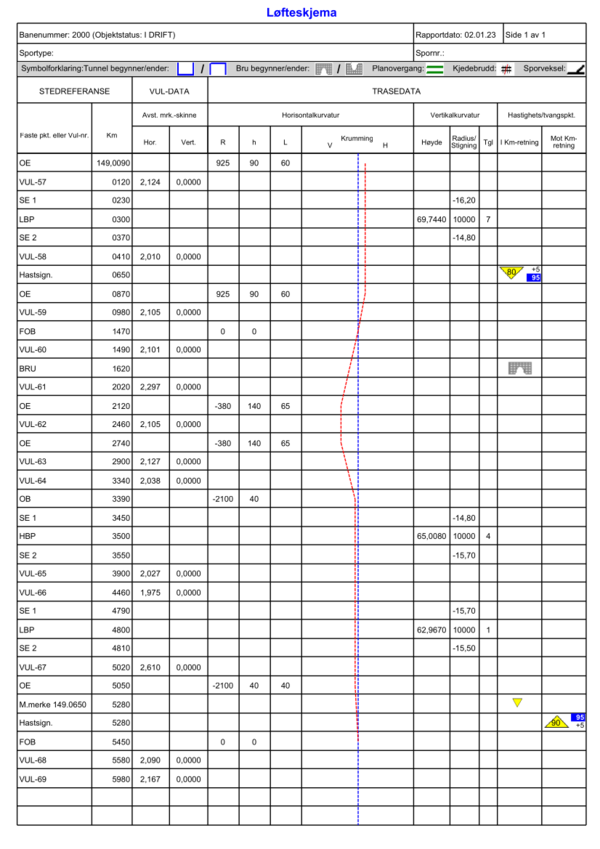
Alle punkt som innebærer endret situasjon på sporet har blitt registrert i infrastrukturregisteret Banedata, sammen med en rekke andre data som berører tekniske anlegg utover traséen, som VUL-punkt, hastighetskilt, planoverganger, bruer og sporveksler. På grunnlag av spordataene fra Banedata kan vi fremstille såkalte løfteskjema. Dette skjemaet inneholder de nødvendige data for justering av sporet med maskin. I tillegg til talldata fra Banedata, inneholder det også en grafisk fremstilling av horisontalkurvaturen ved å illustrere krumningen som negativ og positiv i henholdsvis venstre- og høyrekurver i kilometerretningen. På grunn av fortløpende informasjon om punkter uten direkte sammenheng, rangert etter kilometer, er den grafiske fremstillingen til stor hjelp for å tolke sporets horisontale gang.
Vertikalkurvaturen er også fremstilt med tall i løfteskjemaet, men er ikke presentert grafisk. Dette ville ikke gitt merkbare utslag med den målestokken kilometreringen innebærer i hht. til horisontalkurvaturen.
Figur 40 viser et eksempel på en side fra et løfteskjema fra en delstrekning på Sørlandsbanen, etterfulgt av en forklaring på de ulike elementene som er listet.
| 1. kolonne | traseringspunkt, evt. skilt, mast |
| 2. kolonne | km, 3 desimaler (m-nivå) |
| 3-4. kolonne | evt. VUL-koordinater |
| 5-7. kolonne | horisontalkurvatur: radius (sirkelkurven), overhøyde og lengde på overgangskurve |
| 8. kolonne | grafisk krumningsdiagram |
| 9-11. kolonne | vertikalkurvatur: h.o.h., radius eller stigning og tangentlengde |
| 12-13.kolonne | hastighetsskilter |
5 Vedlegg
5.1 Andre typer overgangskurver
To ikke-lineære overgangskurver:
En 4.gradsparabel har krumningsforløp tilsvarende to 2.gradsparabler. Derfor gjelder ulike matematiske uttrykk for henholdsvis første og siste halvdel og kurvens utstrekning:
| [math]x\lt \frac{l}{2}: y = \frac{x^4}{6Rl^2}[/math] | |
| [math]x\gt \frac{l}{2}: y = \frac{x^4}{6Rl^2}+\frac{x^2}{2R} - \frac{lx}{2R}+\frac{7l^2}{48R}[/math] | (19) |
| [math]m = \frac{l^2}{48R}[/math] |
der l = lengden langs tangenten, og m det såkalte innrykket, eller innflyttingen, som beskrives nærmere i avsnitt 2.5.4.
En annen kurve med s-formet krumning er sinuskurven, gitt som:
| [math]y = \frac{xl}{4R} - \frac{l^2}{2 \pi^2 R}\left(1-\cos\frac{\pi x}{l}\right)[/math] | |
| (20) | |
| [math]m = \frac{l^2}{42,23 R}[/math] |
5.2 Utledning av rettvinklede koordinater på klotoiden
I ligning 23, viste vi en rekkeutvikling av klotoiden til et uttrykk der ordinaten y var en funksjon av buelengden l, etterhvert tilnærmet med x. En mer direkte utledning vil være å rekkeutvikle rettvinklede koordinater x og y hver for seg. Dermed kan vi få uttrykk for koordinatene som funksjoner av enten overgangskurvens lengde eller retning for et vilkårlig punkt.
Vi kan starte med å betrakte enhetsklotoiden: rl = 1
Følgende differensialer gjelder:
- [math]dl = r \,d\tau[/math]
Integrasjon gir:
- [math]\tau = \frac{l^2}{2}[/math]
der τ er den tangentielle retningen i et punkt
For rettvinklede koordinater til punkt på enhetsklotoiden har vi:
- [math]dx = \cos\tau dl \quad dy = \sin\tau dl[/math]
Med dette utgangspunktet får vi følgende kjerner:
- [math]l = \sqrt{2}\sqrt{\tau} \quad \frac{dl}{d\tau} = \frac{1}{\sqrt{2}\sqrt{\tau}} \quad dl = \frac{d\tau}{\sqrt{2}\sqrt{\tau}}[/math]
Dermed får vi følgende differensialer:
[math]dx = \cos\frac{l^2}{2} dl = \frac{1}{\sqrt{2}}\frac{\cos\tau}{\sqrt{\tau}} d\tau \quad dy = \sin\frac{l^2}{2} dl = \frac{1}{\sqrt{2}}\frac{\sin\tau}{\sqrt{\tau}} d\tau[/math]
- som gir disse integralene:
- [math]x = \int_0^l \cos\frac{l^2}{2} dl = \frac{1}{\sqrt{2}}\int_0^\tau\frac{\cos\tau}{\sqrt{\tau}} d\tau \quad y = \int_0^l\sin\frac{l^2}{2} dl = \frac{1}{\sqrt{2}}\int_0^\tau\frac{\sin\tau}{\sqrt{\tau}} d\tau[/math]
For en vilkårlig klotoide gitt med parameter A, får vi:
- [math]\gt x = \int_0^l \cos\frac{l^2}{2A^2} dl = \frac{A}{\sqrt{2}}\int_0^\tau\frac{\cos\tau}{\sqrt{\tau}} d\tau \quad y = \int_0^l\sin\frac{l^2}{2A^2} dl = \frac{A}{\sqrt{2}}\int_0^\tau\frac{\sin\tau}{\sqrt{\tau}} d\tau[/math]
Men disse integralene lar seg ikke løse direkte, og må derfor løses gjennom rekkeutvikling.
Cosinus- og sinusfunksjonen er gitt ved:
- [math]\cos\frac{l^2}{2A^2} = 1 - \frac{l^4}{2^2 \cdot A^4 \cdot 2!} + \frac{l^8}{2^4 \cdot A^8 \cdot 4!} - \frac{l^{12}}{2^6 \cdot A^{12} \cdot 6!} + \dots[/math]
- [math]\sin\frac{l^2}{2A^2} = \frac{l^2}{2A^2} - \frac{l^6}{2^3 \cdot A^6 \cdot 3!} + \frac{l^{10}}{2^5 \cdot A^{10} \cdot 5!} - \frac{l^{14}}{2^7 \cdot A^{14} \cdot 7!} + \dots[/math]
Dermed kan integralene over løses:
- [math]x = l - \frac{l^5}{5\cdot 2^2 \cdot A^4 \cdot 2!} + \frac{l^9}{9\cdot 2^4 \cdot A^8 \cdot 4!} - \frac{l^{13}}{13\cdot 2^6 \cdot A^{12} \cdot 6!} + \dots[/math]
- [math]y = \frac{l^3}{3\cdot 2A^2} - \frac{l^7}{7\cdot 2^3 \cdot A^6 \cdot 3!} + \frac{l^{11}}{11\cdot 2^5 \cdot A^{10} \cdot 5!} - \frac{l^{15}}{15\cdot 2^7 \cdot A^{14} \cdot 7!} + \dots[/math]
Ønskes stigningsvinkelen τ i stedet for buelengden l som parameter i ligningene, kan vi sette inn for [math]l = \sqrt{2\tau}[/math]:
- [math]x = (2\tau)^{1/2} - \frac{(2\tau)^{5/2}}{5\cdot 2^2 \cdot A^4 \cdot 2!} + \frac{(2\tau)^{9/2}}{9\cdot 2^4 \cdot A^8 \cdot 4!} - \frac{(2\tau)^{13/2}}{13\cdot 2^6 \cdot A^{12} \cdot 6!} + \dots[/math]
- [math]x = \sqrt{2\tau} (1 - \frac{\tau^2}{10A^4} + \frac{\tau^4}{216A^8} - \frac{\tau^6}{9360A^{12}} + \dots)[/math]
- [math]y = \frac{(2\tau)^{3/2}}{3\cdot 2A^2} - \frac{(2\tau)^{7/2}}{7\cdot 2^3 \cdot A^6 \cdot 3!} + \frac{(2\tau)^{11/2}}{11\cdot 2^5 \cdot A^{10} \cdot 5!} - \frac{(2\tau)^{15/2}}{15\cdot 2^7 \cdot A^{14} \cdot 7!} + \dots[/math]
- [math]y = \sqrt{2\tau} (\frac{\tau}{3} - \frac{\tau^3}{42A^6} + \frac{\tau^5}{1320A^{10}} - \frac{\tau^7}{75600A^{14}} + \dots)[/math]
Ønskes summenotasjon, kan formlene over skrives som:
- [math]x = \sum_{n=1}^{\infty} (-1)^{n+1} \cdot\frac{l^{4n-3}}{(4n-3)\cdot(2n-2)! 2^{2n-2} \cdot A^{4n-4}}[/math]
- [math]x = \sqrt{2\tau}\sum_{n=1}^{\infty} (-1)^{n+1} \cdot\frac{\tau^{2n-2}}{(4n-3)\cdot(2n-2)! \cdot A^{4n-4}}[/math]
- [math]y = \sum_{n=1}^{\infty} (-1)^{n+1} \cdot\frac{l^{4n-1}}{(4n-1)\cdot(2n-1)! 2^{2n-1} \cdot A^{4n-2}}[/math]
5.3 Beregning av kurveradius på et punkt i en overgangskurve
I beregningene legges til grunn lineær horisontalrampe og lineær overhøyderampe i overgangskurven. Dette er den enkleste beregningsmetode hvor produktet av betraktet lengde på overgangskurve regnet fra OB med tilhørende radius i sirkelkurve er konstant:
[math]\frac{1}{R_{X}\cdot L_{X}}= \frac{1}{R_{OE}\cdot L}[/math]
Som regel er ROE og overgangskurvens lengde L fra OB til OE kjent.
5.3.1 Sporgeometri i kurvesegmentet
Et kurvesegment består normalt av overgangskurve, sirkelkurve og overgangskurve. Overgangskurvens begynnelse betegnes OB og tilsluttende sporelement er vanligvis en rett linje. Men også kurvepunkt FOB forekommer; dvs. at den ene overgangskurven går direkte inn i en ny overgangskurve som er motsatt rettet (for eksempel fra høyre til venstre eller omvendt).
Overgangskurvens ende betegnes OE og tilsluttende sporelement er den rene sirkelkurve.
Overgangskurven har vanligvis form som en klotoide, men kubisk parabel forekommer også. For små lengder av en overgangskurve er kubisk parabel i praksis identisk med klotoide. Det er enklere å regne med kubisk parabel. Det blir derfor i dette dokumentet tatt utgangspunkt i den kubiske parabel mht. beregning for tilordnet radius for det stedet som skal betraktes i overgangskurven. Radius tilhører en sirkel og beskriver derfor en parabel av annen grad. Sirkelen blir dermed tangent til den kubiske parabel og radius vil variere gjennom hele overgangskurven. Radius som tangent er lik radius til sirkelkurve i OE punktet og blir uendelig ved OB punktet ved overgang til den rette linje.
Med utgangspunkt i direkte overgang fra rett linje til sirkelkurve i KP punktet (punkt T i figur 1) vil sirkelkurvens radius være:
[math]R_{m}=R+m1[/math]
Termen m1 er innflyttingen av den opprinnelige sirkelkurve til ny sirkelkurve med radius R:
[math]m1=\frac{L^2}{24\cdot R}[/math]
Ved overgangskurvens ende OE (punkt C i figur 1) skal ordinaten være
[math]y_{OE}=\frac{1}{6}\cdot\frac{L^3}{R\cdot L}=\frac{1}{6}\cdot\frac{L^2}{R}=4m1[/math]
Det vises til figur 1.
Kontroll for beregning av radius i sirkelkurve ved OE punktet (punkt C i figur 1):
[math]4m1\cdot 6\cdot R=L^2[/math]
[math]R=\frac{1}{24}\cdot\frac{L^2}{m1}[/math]
Overgangskurvens lengde L (abscisse i figur 1) er symmetrisk om KP punktet (T – punktet i figur 1) med samme lengde til hver side (av KP punktet). Innrykket ved KP punktet for overgangskurve til sirkel med radius R skal være:
[math]y_{KP}=\frac{1}{6}\cdot\frac{\left ( \frac{L}{2} \right )^3}{R\cdot L}=\frac{1}{6}\cdot\frac{\frac{L^2}{8}}{R}=\frac{1}{48}\cdot\frac{L^2}{R}=\frac{1}{2}m1 [/math]
Figur 1: Overgangskurve med innrykk
Figur 2: Overgangskurve med krumning og overhøyderampe
Under antakelse om lineær rampe i horisontalplanet beregnes kurveradius i KP punktet under hensyntagen til innrykket:
[math]\frac{1}{R_{KP}}=\frac{\frac{L}{2}}{R\cdot L}[/math]
[math]R_{KP}\cdot\frac{1}{2}\cdot L=R\cdot L[/math]
[math]R_{KP}=2\cdot R[/math]
Radius som tangent til kubisk parabel i KP punktet er dobbelt så stor som radius ved OE punktet.
Ved et punkt x blir innrykket tilsvarende med utgangspunkt i sirkelkurve med radius R i OE:
[math]y_{X}=\frac{1}{6}\cdot\frac{{L^3}_X}{R\cdot L}[/math]
Tilhørende radius som er tangent for parabel i punktet i x:
[math]\frac{1}{R_{X}}=\frac{L_X}{R\cdot L}[/math]
Dette gir:
[math]R_{X}=\frac{R\cdot L}{L_X}[/math]
Det legges også til grunn en lineær betraktning av stigningen eller fallet i overhøyderampen i overgangskurven.
[math]h_{X}=h\cdot\frac{L_X}{L}[/math]
Med dette er grunnlaget utført for å kunne beregne parametere ved ønsket sted i overgangskurven.
Dette skal belyses ved et eksempel.
Overgangskurven har en lengde L = 58 m. Overhøyde i sirkelkurve er h = 145 mm. Radius i sirkelkurve er R = 295 m.
Stigningsgradienten er:
[math]s=\frac{145}{58}=2.5 ‰[/math], dvs. 2.5 mm/m
Innrykket ved OE punktet:
[math]y_{OE}=\frac{1}{6}\cdot\frac{L^3}{R\cdot L}=\frac{1}{6}\cdot\frac{L^2}{R}=4m1[/math]
[math]4m1=\frac{L^2}{6\cdot R}=\frac{58^2}{6\cdot 295}=1.90 m[/math]
I OE punktet er kurveradius:
[math]R_{OE}=295m[/math]
Innrykket i KP punktet til overgangskurven:
[math]\frac{1}{2}\cdot m1=0.24m[/math]
Kurveradius i KP punktet:
[math]R_{KP}=2\cdot R=2\cdot 295=590m[/math]
Overhøyde i KP punktet er:
[math]h_{KP}=h\cdot\frac{L_{KP}}{L} =145\cdot\frac{29.00}{58.00}=73mm[/math]
Det velges et sted fra OB punktet LX = 37.00 m.
Ved dette stedet er overhøyden i overhøyderampen:
[math]h_{X}=h\cdot\frac{L_{X}}{L} =145\cdot\frac{37.00}{58.00}=93mm[/math]
Kurveradius i dette punktet er:
[math]R_{X}=\frac{R\cdot L}{L_{X}} =\frac{295.00\cdot 58.00}{37.00}=463m[/math]
Innrykket er:
[math]y_{X}=\frac{L^3_{X}}{6\cdot R\cdot L} [/math]
[math]y_{X}=\frac{37.00^3}{6\cdot 295\cdot 58}=0.49m [/math]
5.3.2 Beregning av tilhørende radius på et hvert sted i overgagskurve mellom 2 sirkelkurver
Beregning av RX på et sted i overgangskurve mellom 2 sirkelkurver. Det vises til figur:
Mellom 2 ensrettede sirkelkurver med ulik radius kan parameteren A beregnes når følgende parametere er kjent:
- Overgangskurvens lengde:L12
- Radius i sirkelkurve 1: R1
- Radius i sirkelkurve 2: R2
Det legges til grunn at R2 < R1
Parameterverdiene kan hentes fra løfteskjema.
Generelt uttrykkes relasjon mellom A, RX og LX i en overgangskurve hvor A er en konstant faktor i en klotoide:
[math]A=\sqrt{R_{X}\cdot L_{X}}[/math]
LX er lengde fra OB punkt til betraktet sted i overgangskurven og RX er tilhørende radius. Formelen uttrykker at jo lengre LX er, jo mindre blir RX. Videre utledes:
[math]A^2=R_{X}\cdot L_{X}[/math]
[math]R_{X}=\frac{A^2}{ L_{X}}[/math]
For overgangskurve mellom 2 ensrettede kurver gjelder følgende relasjon:
[math]L_{12}=\frac{A^2}{R_{2}}-\frac{A^2}{R_{1}}[/math]
Det gjelder at
R2 < R1
I et løfteskjema er parameterne R1, R2 og L12 kjent. Formelen løses mht. A:
[math]L_{12}\cdot R_{1}\cdot R_{2}=A^2 \cdot (R_{1}-R_{2}) [/math]
[math]A^2=\frac{L_{12}\cdot R_{1}\cdot R_{2}}{R_{1}-R_{2}}[/math]
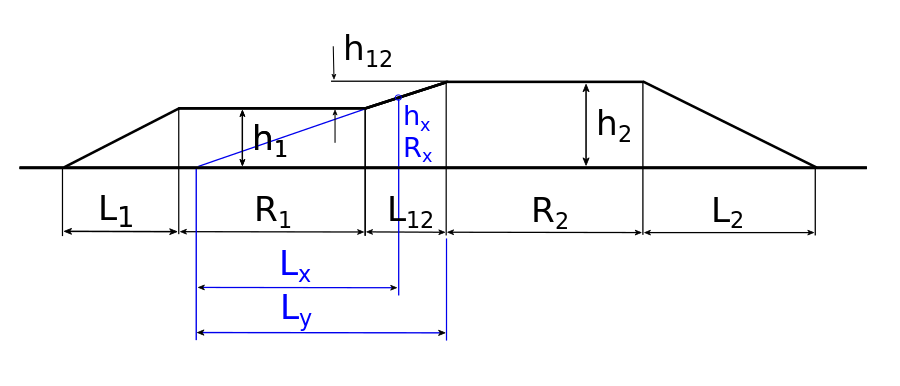
Det er ønskelig å beregne parameterne Lx og Ly med grunnlag i overhøydene i sirkelkurvene R1 og R2. Den blå stiplede linjen er forlengelse av overgangskurve L12 til nullinje. Gjennom parameterne h2, h1 og L12 er gradienten kjent. Forlengelse av gradienten til overgangskurven til nullpunktet beregnes, se figur på side 5:
[math] \frac{h_{2}-h_{1}}{L_{12}}=\frac{h_{2}}{L_{Y}}[/math]
Formel løses mht. LY:
[math]L_{Y}=\frac{L_{12}\cdot h_{2}}{h_{2}-h_{1}}[/math]
LX fastsettes ut fra hvor radius til den mellomliggende overgangskurve fra OB punktet til sirkelkurve med radius R1 skal beregnes.
Når parameter A2 er beregnet iht. ovennevnte formel, kan det være hensiktsmessig å utføre en kontroll ved å beregne L12:
[math]L_{12}=\frac{A^2}{R_{2}}-\frac{A^2}{R_{1}}[/math]
Det er nødvendig å beregne en fiktiv lengde av overgangskurve LY FIKTIV relatert til sirkelkurve med radius R1:
[math]{L_{Y}}_{FIKTIV}=\frac{A^2}{R_{1}}[/math]
LY FIKTIV må ikke forveksles med LY. LY er beregnet lengde fra OE punkt til sirkelkurve med radius R2 til antatt OB punkt for sirkelkurve med radius R1. LY FIKTIV er beregnet iht. formel over.
Det utføres en kontroll ved å beregne radius R1 i overgangspunktet til mellomliggende overgangskurve (begynnelse av overgangskurven):
[math]R_{1}=\frac{A^2}{{L_{Y}}_{FIKTIV}}[/math]
Det utføres også en kontroll ved å beregne radius R2 i ende av mellomliggende overgangskurve hvor R2 < R1. Den resulterende lengde av den fiktive overgangskurve for sirkelkurve med R2 blir:
[math]L_{RES,Y}={L_{Y}}_{FIKTIV}+L_{12}[/math]
Det legges merke til at LRES, Y er summen av den fiktive lengde LY FIKTIV og den reelle lengde L12.
Radius R2 i sirkelkurve blir:
[math]R_{2}=\frac{A^2}{L_{RES,Y}}[/math]
Dersom kontrollberegningene viser riktige resultat, kan radius til et vilkårlig sted på mellomliggende overgangskurve beregnes:
Avstand fra OE punktet til radius R2 til betraktet sted:
[math]\vartriangle L_{X}[/math]
Den fiktive lengde av overgangskurve til radius RX blir:
[math]L_{X}=L_{RES,Y}-\vartriangle L_{X}[/math]
Radius RX beregnes:
[math]R_{X}=\frac{A^2}{L_{X}}[/math]
Med beregnet A2 kan tilsluttende radius i et vilkårlig sted i den mellomliggende overgangskurve beregnes.
Metoden vil alltid fungere ved framgangsmåte som vist; dvs. at kurve med minste radius og kurve med største radius får plass i beregningshierarkiet som forklart.. I det etterfølgende utføres beregninger for 3 ulike kurvesegment som er hentet fra løfteskjemaer.
Følgende opplysninger foreligger:
OE ved km 119,2138 for minste kurveradius
OB ved km 119,2538 for minste kurveradius lik OE for største kurveradius
Lengde av mellomliggende overgangskurve [math]L_{12}= 40 m[/math]
[math]R_{2}= 248 m[/math]
[math]R_{1}= 400 m[/math]
Beregne A2:
[math]A^2=\frac{L_{12}\cdot R_{1}\cdot R_{2}}{R_{1}-R_{2}}=\frac{40\cdot 248\cdot 400}{400-248}=\frac{3968000}{152}=26105[/math]
Kontroll av overgangskurvens lengde:
[math]L_{12}=\frac{A^2}{R_{2}}-\frac{A^2}{R_{1}} [/math]
[math]L_{12}=\frac{26105}{248}-\frac{26105}{400}=105,26-65,26=40m [/math](er o.k.)
Beregning av fiktiv lengde av overhøyderampe LY:
[math]{L_{Y}}_{FIKTIV}=\frac{A^2}{R_{1}}[/math]
[math]{L_{Y}}_{FIKTIV}=\frac{26105}{400}=65,26m[/math]
Kontroll for sirkelkurve med radius R1 i overgang til mellomliggende overgangskurve:
[math]R_{1}=\frac{A^2}{{L_{Y}}_{FIKTIV}}=\frac{26105}{65,26}=400m[/math](er o.k.)
Kontroll for sirkelkurve med radius R2 i overgang til mellomliggende overgangskurve i OE2:
[math]L_{12}=119,2138-119,2538=\left |40\right |m[/math]
Resulterende lengde:
[math]L_{RES,Y}={L_{Y}}_{FIKTIV}+L_{12}[/math]
[math]L_{RES,Y}=65,26+40,00=105,26[/math]
[math]R_{2}=\frac{A^2}{L_{RES,Y}}=\frac{26105}{105,26}=248m[/math](er o.k.)
Beregning ved km 119,2338:
[math]\vartriangle L_{X}=119,2138-119,2158=\left |2\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{26105}{105,26-2,00}=252,80m[/math]
Kontroll:
[math]A^2=R\cdot (L_{RES,Y}-\vartriangle L_{X})=252,80\cdot 103,26=26105m[/math] (er o.k.)
Beregning ved km 119,2518:
[math]\vartriangle L_{X}=119,2138-119,2118=\left |38\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{26105}{105,26-38,00}=388,10m[/math]
Kontroll:
[math]A^2=R_{X}\cdot (L_{RES,Y}-\vartriangle L_{X})=388,10\cdot 67,26=26105m[/math] (er o.k.)
Beregning ved km 119,2338:
[math]\vartriangle L_{X}=119,2138-119,2338=\left |20\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{26105}{105,26-20,00}=306,20m[/math]
Kontroll:
[math]A^2=R_{X}\cdot (L_{RES,Y}-\vartriangle L_{X})=306,20\cdot 85,26=26105m[/math] (er o.k.)
OE2 ved km 12,5847
OB ved km 12,6287
L = 44 m
[math]h_{1} = 15 mm[/math]
[math]h_{2} = 110 mm[/math]
[math]R_{2} = 370 m[/math]
[math]R_{1} = 1500 m[/math]
[math]A^2=\frac{L_{12}\cdot R_{1}\cdot R_{2}}{R_{1}-R_{2}}=\frac{44\cdot 1500\cdot 370}{1500-370}=21611[/math]
Kontroll av overgangskurvens lengde:
[math]L_{12}=\frac{A^2}{R_{2}}-\frac{A^2}{R_{1}} [/math]
[math]L_{12}=\frac{21611}{370}-\frac{21611}{1500}=58,41-14,41=44m [/math](er o.k.)
Beregning av fiktiv lengde av overhøyderampe LY:
[math]{L_{Y}}_{FIKTIV}=\frac{A^2}{R_{1}}[/math]
[math]{L_{Y}}_{FIKTIV}=\frac{21611}{1500}=14,41m[/math]
[math]R_{1}=\frac{A^2}{{L_{Y}}_{FIKTIV}}=\frac{21611}{14,41}=1500m[/math](er o.k.)
Kontroll i OE2:
[math]L_{12}=112,5847-112,6287=\left |44\right |m[/math]
Resulterende lengde:
[math]L_{RES,Y}={L_{Y}}_{FIKTIV}+L_{12}[/math]
[math]L_{RES,Y}=14,41+44,00=58,41[/math]
[math]R_{2}=\frac{A^2}{L_{RES,Y}}=\frac{21611}{58,41}=370,00m[/math](er o.k.)
Beregning ved km 12,5837:
[math]\vartriangle L_{X}=12,5847-12,5857=\left |1\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{21611}{58,41-1,00}=376,43m[/math]
Kontroll:
[math]A^2=R\cdot (L_{RES,Y}-\vartriangle L_{X})=376,43\cdot 57,41=21611m[/math] (er o.k.)
Beregning ved km 12,6277:
[math]\vartriangle L_{X}=12,5847-12,6277=\left |43\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{21611}{58,41-43,00}=1402m[/math]
Kontroll:
[math]A^2=R_{X}\cdot (L_{RES,Y}-\vartriangle L_{X})=1402,40\cdot 15,41=21611[/math] (er o.k.)
Beregning ved km 12,6007:
[math]\vartriangle L_{X}=12,587-12,6007=\left |16\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{21611}{58,41-16,00}=509,60m[/math]
Kontroll:
[math]A^2=R_{X}\cdot (L_{RES,Y}-\vartriangle L_{X})=509,6\cdot 42,41=21611[/math] (er o.k.)
Fra banenummer 0630:
OE2 ved km 58,6390
OB ved km 58,6890
L = 50 m
h1 = 130 mm
h2 = 150 mm
R2 = 250 m
R1 = 500 m
Beregning av parameter A2:
[math]A^2=\frac{L_{12}\cdot R_{1}\cdot R_{2}}{R_{1}-R_{2}}=\frac{50\cdot 500\cdot 250}{1500-370}=25000[/math]
Kontroll av overgangskurvens lengde:
[math]L_{12}=\frac{A^2}{R_{2}}-\frac{A^2}{R_{1}} [/math]
[math]L_{12}=\frac{25000}{250}-\frac{25000}{500}=100,00-50,00=50,00m [/math](er o.k.)
Beregning av fiktiv lengde av overhøyderampe LY:
[math]{L_{Y}}_{FIKTIV}=\frac{A^2}{R_{1}}[/math]
[math]{L_{Y}}_{FIKTIV}=\frac{25000}{500}=50,00m[/math]
[math]R_{1}=\frac{A^2}{{L_{Y}}_{FIKTIV}}=\frac{25000}{50,00}=500m[/math](er o.k.)
Kontroll i OE2:
[math]L_{12}=58,6390-58,6890=\left |50\right |m[/math]
Resulterende lengde:
[math]L_{RES,Y}={L_{Y}}_{FIKTIV}+L_{12}[/math]
[math]L_{RES,Y}=50,00+50,00=100,00[/math]
[math]R_{2}=\frac{A^2}{L_{RES,Y}}=\frac{25000}{100,00}=250,00m[/math](er o.k.)
Beregning ved km 12,5837:
[math]\vartriangle L_{X}=58,6390-58,6400=\left |1\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{25000}{100,00-1,00}=252,53m[/math]
Kontroll:
[math]A^2=R\cdot (L_{RES,Y}-\vartriangle L_{X})=252,53\cdot 99,00=25000m[/math] (er o.k.)
Beregning ved km 58,688:
[math]\vartriangle L_{X}=58,6390-58,6880=\left |49\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{25000}{100,00-49,00}=490,20m[/math]
Kontroll:
[math]A^2=R_{X}\cdot (L_{RES,Y}-\vartriangle L_{X})=490,20\cdot 51,00=25000[/math] (er o.k.)
Beregning ved km 58,6550:
[math]\vartriangle L_{X}=58,6390-58,6550=\left |16\right |m [/math]
[math]R_{X}=\frac{A^2}{{L_{Y}}_{FIKTIV}-\vartriangle L_{X}}=\frac{25000}{100,00-16,00}=297,62m[/math]
Kontroll:
[math]A^2=R_{X}\cdot (L_{RES,Y}-\vartriangle L_{X})=297,62\cdot 84,00=25000[/math] (er o.k.)
6 LITTERATURHENVISNINGER
- Esveld, Coenraad, Dr. Modern Railway Track, (1989)
- Haacke, W. et al. Matematik für Bauingeniuere (1968)
- Heje, Kolbjørn Vei og jernbanebygging, Håndbok for undervisning og praksis, H. Aschehaug & CO, 837s. (1941)
- Holme, Jan Sporveksler, Fag 34045 Jernbaneteknikk VK, NTNU, notat nr. 856 (1993)
- Holom, Finn Kurs i baneteknikk; Sporets geometri, NSB Bane, Region Øst (1992)
- Skoglund, Kjell Arne & Våge, John Traseringsparametre og kjørekomfort, Fag 34045 Jernbaneteknikk VK, NTNU, notat nr. 1027 (jan. 1997)
- Skoglund, Kjell Arne Sporgeometri og kjøredynamikk, Fag 34045 Jernbaneteknikk VK, NTNU, notat nr. 955 (mars 1996)
- Jernbaneverket Overbygning-Prosjektering, Teknisk regelverk JD 530 (01.01.98)
- Jernbaneverket Overbygning-Bygging, Teknisk regelverk JD 531 (01.01.98)
- Jernbaneverket Overbygning-Vedlikehold, Teknisk regelverk JD 532 (01.01.98)
- Mathisen, Olav Kurvestikking, ILM-Ås (1987)
- NSB Lærebok for linjepersonalet, Trykk 383, Tjenesteskrifter NSB Hovedadministrasjonen, NSB Jernbaneskolen (1987)
- NSB Overbygningsnormaler, Trykk 380
- NSB Banetekniske forutsetninger for togfremføringen, Trykk 302.1 (01.09.85)
- Banverket Spårgeometrihandboken, BVH 586.40 (01.12.96)
- Banverket Växelprojekteringshandboken, BVH 586.45 (01.04.95)
- DSB Sporregler, tillæg 2A-2F (1987)