Dimensjoneringsmetoder

1 OVERBYGNINGENS KOMPONENTER

Sporets overbygning består av flere komponenter med ulike oppgaver:

1. Skinner hvor skjøter inkluderes. Skinnene har 2 oppgaver:

• Fungere som kjørevei for det rullende materiell
• Fungere som bærebjelke for det rullende materiell

2. Befestigelsen som omfatter :

• Klemfjærer
• Mellomleggsplate
• Isolatorer

Befestigelsessystemet som enhet skal sikre et forsvarlig feste av skinnen til svillen og hindre forskyvning (skinnevandring) og velting av skinnen når det rullende materiell passerer.

Klemfjærene skal feste skinnen til svillen ved utøvelse av en nominell klemkraft. Det er av betydning at klemfjærene er konstruert slik at de har en lang oppspenningsveg. Dette er nødvendig for at klemkraften også blir tilstrekkelig stor nok ved f. eks. slitte isolatorer.

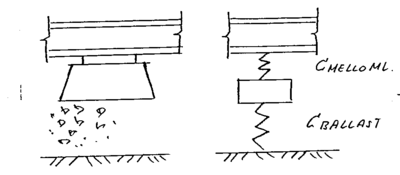
Mellomleggsplatene består av et elastisk materiale som har til oppgave å dempe spissbelastningene ved passering av det rullende materiell. Dette er spesielt nødvendig for betongsviller. Mellomleggsplatene skal også hindre skinnevandring

Isolatorene skal isolere signal- og kjørestrøm.

3. Sviller (betong- og tresviller), i svillene inngår :

• Innstøpte skuldre (ankere) i betongsviller
• Skrudde forbindelser i tresviller

Svillene må overføre krefter fra det rullende materiell til ballasten.

De innstøpte ankerne i betongsvillene og de skrudde forbindelsene i tresvillene utgjør forbindelsen mellom svillen og befestigelsen.

4. Ballast(pukk).

Ballasten skal overføre belastningene fra svillen til undergrunnen. Det må benyttes pukk og det stilles bestemte krav til dette materialet mht. fraksjonering og kornform. For å oppnå en jevn fordeling av belastningen og for å tilfredsstille kravet til ønsket sidemotstand i helsveist sporer det nødvendig at kornformen er mest mulig kubisk.

5. Sporveksler som er en spesiell overbygningskomponent med mange delkomponenter.

Sporveksler er en komponent som forbinder spor med hverandre slik at et rullende materiell uten avbrudd ved fremføring kan skifte fra et spor til et annet.

Hver av komponentene har iht. ovennevnte punkter spesielle oppgaver. Komponentene må være dimensjonert hver for seg og også i forhold til hverandre slik at sporet danner en pålitelig og sikker kjørevei for det rullende materiell. De må samlet kunne virke som en enhet.

I det etterfølgende skal de krefter som angriper sporet, belyses. Videre beskrives dimensjoneringen av de enkelte overbygningskomponentene hver for seg og samlet. Hensikten er å gi et bilde av de krav som må stilles til overbygningen for å oppnå tilstrekkelig sikkerhet og pålitelighet ved framføring av det rullende materiell.

2 KREFTER MOT SPORET

De krefter som virker mot sporet ved kjøring av det rullende materiell, er :

• De vertikale krefter på grunn av aksellaster.

• De laterale krefter(føringskrefter) som oppstår spesielt ved kjøring i kurver.

• Langsgående krefter som oppstår ved bremsing av det rullende materiell i

sporet.

• Langsgående krefter som forårsakes av temperaturendringer. Disse

kreftene kan i helsveist spor bli meget store.

I dette heftet behandles de vertikale og laterale krefter og hvordan disse påvirker overbygningen.

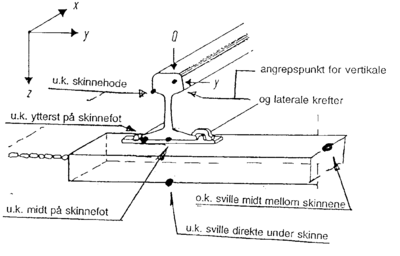
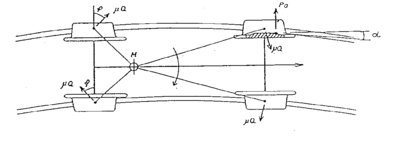
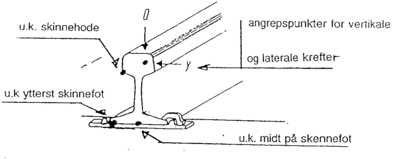
I figur 4.1 nedenfor er vist hvordan de vertikale og laterale krefter normalt angriper skinnehodet på skinnen. Videre er antydet steder på skinneprofilet og på svillen som blir utsatt for store påkjenninger ved belastning.

Figur 4.1 Vertikale og laterale krefter som angriper skinnehodet. Steder på skinneprofilet samt sville som blir utsatt for store påkjenninger.

3 TYPER AV VERTIKALE OG HORISONTALE KREFTER

De vertikale krefter inndeles i :

• Statiske krefter på grunn av aksellaster. Disse kreftene kan betraktes som

konstant for en gitt stillestående vogn eller et stillestående lokomotiv.

• Kvasistatiske krefter som for en gitt vogn eller et lokomotiv normalt øker

med økede hastigheter, idet vesentligste på grunn av sentrifugalkraften. Dessuten er sporgeometrienav betydning.

• Dynamiske krefter som forårsakes av ujevnheter i sporet. Disse kreftene er

impuls- og vibrasjonskrefter som stiger raskt med økede hastigheter.

De horisontale krefter inndeles i :

• Kvasistatiske krefter som øker med økede hastigheter. Sporgeometrien

influerer også på størrelsen av de kvasistatiske krefter.

• Dynamiske krefter som også forårsakes av ujevnheter i sporet. Disse

kreftene stiger med økede hastigheter.

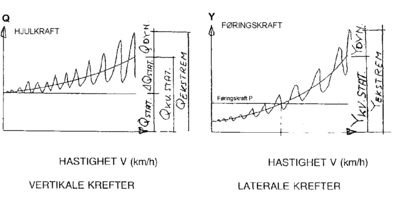
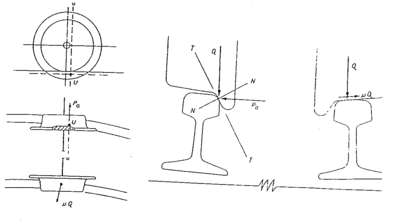
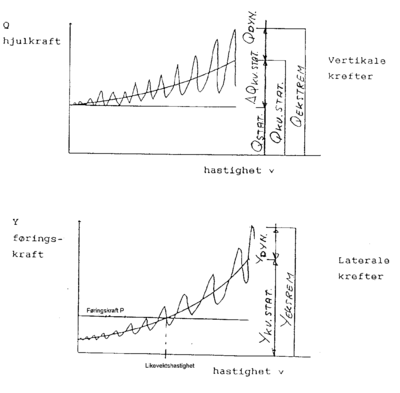
Av spesiell interesse er den såkalte styrekraft. Denne er en kvasistatisk friksjonskraft som normalt er konstant ved varierende hastigheter og er årsak til slitasje på skinnehodet.

De ulike kreftene er vist grafisk i figur 4.2.

Figur 4.2 De forskjellige krefter som funksjon av hastighet.

4 BEREGNING AV STATISKE KREFTER

4.1 Statisk hjulkraft

Med en gitt nominell aksellast P blir den vertikale statiske hjulkraftQ0under forutsetning av symmetri :

[math] Q_0 = {P \over 2} [kN] [/math]

(4.1)

4.2 Kvasistatisk tilleggskraft

Normalt inntreffer forhold som bevirker tilleggskrefter ved framføring av det rullende materiell i sporet :

• Tilleggskrefter forårsaket av forandring av hjultrykket på grunn av

overhøyde. Disse kreftene oppstår på grunn av sentrifugalkraften og skyldes bare sporet. Ved kjøring med hastighet som er større enn den såkalte likevektshastighet, virker tilleggskreftene på ytterstreng. Ved framføring med hastighet lavere enn likevektshastigheten er det innerstreng som blir utsatt for tilleggsbelastningen.

• Tilleggskrefter forårsaket av eksentrisk belastning. Det rullende materieller

i hovedsak konstruert slik at hjulsatsen fordeler belastningen fra egenvekten likt på begge hjulene. Den eksentriske belastning skyldes derfor i det vesentligste usymmetrisk lagret godslast.

• Tilleggskrefter forårsaket av forandring av hjultrykk i vindskjevt spor. Disse

kreftene skyldes sporets geometri og vognens konstruktive utførelse. Dette betyr at vognens samlede torsjonsstivhet får betydning.

Disse tilleggskreftene benevnes samlet det kvasistatiske tillegget og uttrykkes gjerne i forhold til den statiske hjulkraft Q₀. Det kvasistatiske tillegget ÄQ antas å være i området 0,10 x Q₀< ?Q < 0,30 x Q₀ og bør vurderes for hver banestrekning. I spor med kurverike strekninger med små radier og stor overhøydeantar ?Q større verdier enn på øvrige spor. Det kvasistatiske tillegget er også en funksjon av hastigheten uttrykt gjennom sentrifugalkraften og øker med økede hastigheter.

Den kvasistatiske hjulkraft kan derved uttrykkes ved :

[math] Q_{KV.STAT.} = (Q_0 + \Delta Q)[kN] [/math]

(4.2)

I tillegg opptrer vindkrefter som på fjellstrekningene kan bli meget store. I det etterfølgende vises den statiske hjulkraft og de forskjellige kvasistatiske tilleggene.

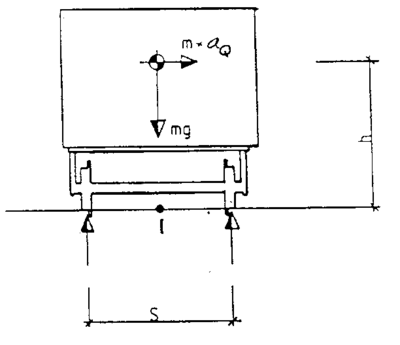
4.3 Kraftbilde ved kjøring av det rullende materiell mot sporet

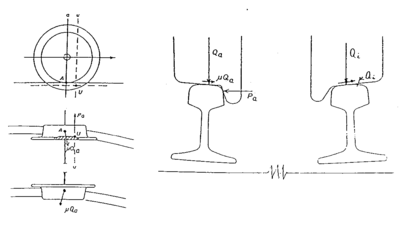
4.3.1 Statisk hjulkraft Q₀

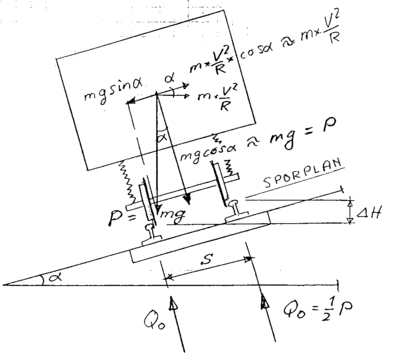
Under forutsetning av fremføring av det rullende materiell med likevektshastighet blir kraftbildet som vist under. Det utledes at denne tilstanden opptrer når :

[math] m \cdot g \cdot \sin \alpha = m \cdot \cos \alpha \cdot {V^2 \over R} \approx m \cdot {V^2 \over R} [/math]

(4.3)

hvor sin α= D/s

Da vinkelen α er meget liten, kan cos α settes lik 1,0.

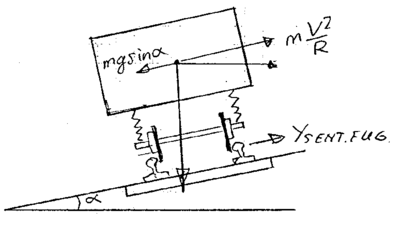
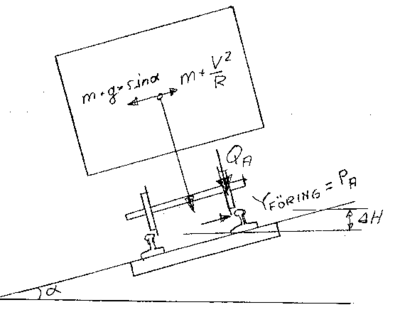
Det legges merke til at komponentene m·g·sinα og m·V²/R er parallelle med sporplanet.

Figur 4.3 Kraftbilde ved beregning av statisk hjulkraft Q_o ved fremføring med likevektshastighet.

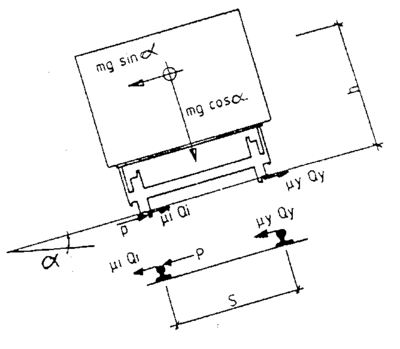
4.3.2 Sentrifugalkraftens innflytelse

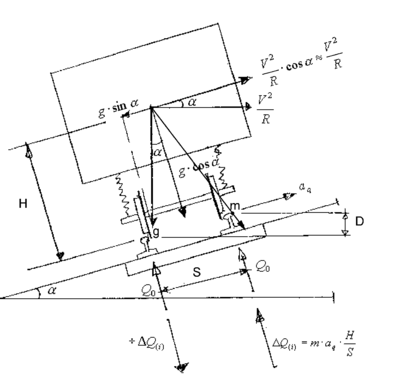
Ved fremføring med hastighet større enn likevektshastigheten dvs. når

[math] \Delta Q_{(i)} = m \cdot a_Q \cdot {H \over s} [/math]

(4.5)

hvor

[math] a_Q = \left( {v^2 \over R} \right)- g \cdot {D \over s} [/math]

(4.6)

a_Q er ukompensert sideakselerasjon i sporplanet. Samtidig blir det en tilsvarende avlastning på innerstreng.

Figur 4.4 Kraftbilde ved beregning av den kvasistatiske tilleggskraft ΔQ på grunn av sentrifugalkraftens innflytelse. Kurve med konstant overhøyde.

4.3.3 Kjøring i lav hastighet

Ved fremføring med hastighet < likevektshastigheten dvs. når

[math] m \cdot g \cdot \sin \alpha \gt m \cdot {v^2 \over R} [/math]

(4.7)

blir innerstreng belastet med en kvasistatisk tilleggskraft som beregnes til:

[math] \Delta Q_{(i)} = m \cdot a_Q \cdot {H \over s} [/math]

(4.8)

hvor

[math] a_Q = g \cdot { \Delta H \over s } - { v^2 \over R} [/math]

(4.9)

a_Q er ukompensert sideakselerasjon i sporplanet. Samtidig blir det en tilsvarende avlastning på ytterstreng.

Figur 4.5 Kraftbilde ved beregning av den kvasistatiske tilleggskraft ΔQ på grunn av lav hastighet. Kurve med konstant overhøyde.

4.3.4 Eksentrisk belastning

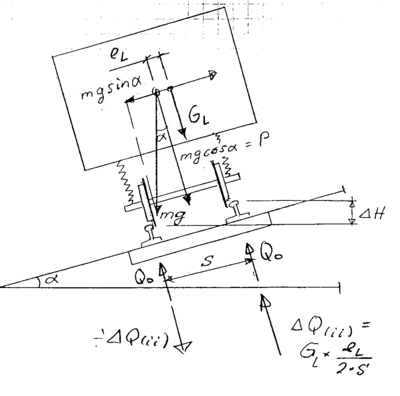
En skinnestreng kan bli belastet med en kvasistatisk tilleggskraft forårsaket av eksentrisk lagret godslast. Denne tilleggskraften beregnes til :

[math]\Delta Q_{ (ii)} = G_L \cdot { e_L \over (2 \cdot s)} [/math]

(4.10)

hvor G_L er eksentrisk plassert godslast og e_L avstand fra vognmidt til lastens angrepspunkt.

Tilleggsbelastning på en skinne vil føre til tilsvarende avlastning på den andre skinnen.

Ved symmetrisk lagret godslast blir belastningen på begge hjulene like store og beregnes til G_L/2.

Figur 4.6 Kraftbilde ved beregning av den kvasistatiske tilleggskraft ΔQ ved eksentrisk plassert godslast.

4.3.5 Vindskjevt spor

I vindskjevt sporoppstår tilleggskrefter på grunn av selve vindskjevheten og vognens torsjonsstivhet. Denne tilleggskraften kan uttrykkes ved:

[math]\Delta Q_{ (iii)} = stign \cdot C_{tA} [/math]

(4.11)

hvor C_tA er vognens totale torsjonsstivhet uttrykt i kN/‰ . Denne faktoren kan i stor grad influeres av vognbyggeren. I formelen over betyr stign. vindskjevheten i ‰.

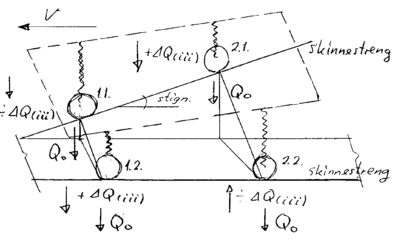
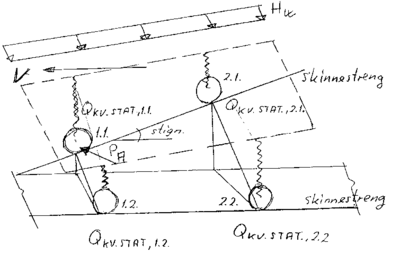
Det fremgår av nedenstående figur at ΔQ_(iii) forårsaker en avlastning av hjulkraften på ytre skinnestreng i det vindskjeve sporet av det hjulet som befinner seg på det laveste punktet på denne skinnestrengen. Det samme forholdet gjør seg gjeldende for hjul nr. 2.2. For øvrige hjul fører denne tilleggskraften til en økning av hjulkraften. Forholdet gjelder ved lav hastighet.

Figur 4.7 Kraftbilde ved beregning av den kvasistatiske tilleggskraft ΔQ i et vindskjevt spor. Vognens torsjonsstivhet har også betydning. Fortegnene for ΔQ angir avlastning( - ) og pålasting( + ) ved lav hastighet.

4.3.6 Vindkrefter

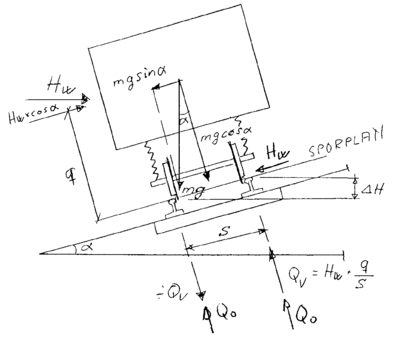
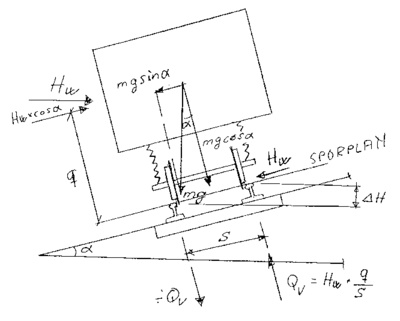
Vindkraftener en horisontal virkende kvasistatisk kraft som betyr pålasting for den ene skinnestrengen og tilsvarende avlastning for den andre skinnestrengen. Med betegnelsen H_W for vindkraft kan det for den kvasistatiske tilleggskraft mot den ene skinnestrengen utledes at:

[math]\Delta Q_{ (V)} = H_W \cdot \cos \alpha \cdot {q \over s} \approx H_W \cdot {q \over s} [/math]

(4.12)

da cosα kan settes lik 1,0. q er avstanden fra vognkassens tyngdepunkt til spormidt i sporplanet og s er sporvidden.

Samtidig vil den andre skinnestrengen få en tilsvarende avlastning.

Figur 4.8 Kraftbilde ved beregning av den kvasistatiske tilleggskraft Q_v på grunn av vindbelastning.

4.3.7 Samlet kraftbilde

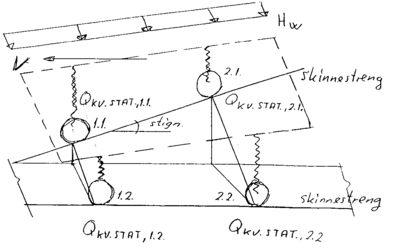
I figur 4.9 gis en oversikt over en mulig lastkombinasjon av de vertikale kvasistatiske krefter samt vindkraft sammen med den statiske hjulkraftQ0i et vindskjevt spor ved lav fremføringshastighet. Fremføringshastigheten i eksemplet forutsettes å være mindre enn likevektshastigheten. Eksentrisk lagret gods bevirker for de nedenstående ligningene pålasting på indre skinnestreng:

• Hjulkraft på ytre skinnestreng av det hjulet som befinner seg lavest : Q_KV.STAT.,1.1 = Q₀ - ΔQ_{( i )} - ΔQ_{( ii )} - ΔQ_{( iii )} - ΔQ_{(V )}

• Hjulkraft på ytre skinnestreng av det hjul som befinner seg høyest : Q_{KV.STAT. ,2.1} = Q₀ - ΔQ _{( i )} - ΔQ_{( ii )} + ΔQ_{( iii )} - ΔQ_{( V )}

• Hjulkraft på indre skinnestreng av det hjulet som befinner seg forrest : Q_{KV.STAT. , 1.2} = Q₀+ ΔQ_{( i )} + ΔQ_{( ii )} + ΔQ_{( iii )} + ΔQ_{( V )}

• Hjulkraft på indre skinnestreng av det hjulet som befinner seg bakerst: Q_{KV.STAT. , 2.2} = Q₀+ ΔQ_{( i )} + ΔQ_{( ii )} + ΔQ_{( iii )} + ΔQ_{( V )}

Figur 4.9 Samlet kraftbilde av den statiske hjulkraft samt alle kvasistatiske tilleggskrefter av alle hjul og vindkraft for en to-akslet vogn i et vindskjevt spor ved lav hastighet. Lastkombinasjonen er kun en av mange mulige kombinasjoner.

5 ZIMMERMANNS METODE (KVASISTATISK TILSTAND)

5.1 Innledning

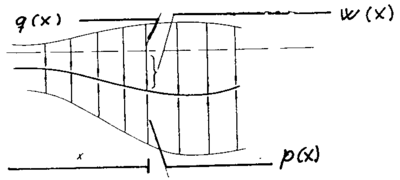
Mht. dimensjonering av overbygningen legges til grunn teorien for en bjelke som er kontinuerlig opplagret på et jevnt elastisk underlag og hvor bøyelinjen for denne bjelken beregnes under belastning. Bjelkens bøyelinje beskrives gjennom følgende differensialligning av 4. grad :

[math] E \cdot I_{X-X} \cdot \left( { d^4 w \over dx^4 } \right) + p(x) = q(x) [/math]

(4.13)

• E·I_{X - X} er stivheten til skinnen om den sterke akse

• w(x) er vertikal nedbøyning av skinnen ved stedet x

• q(x) er hjullasten betraktet som en jevnt fordelt last

• p(x) er det kontinuerlige kontakttrykket mellom sviller og ballastsengen

Det vises til figur 4.10.

Figur 4.10 Bjelkens bøyelinje.

For selve ballastlaget kan ifølge Winkler - hypotesen følgende relasjon dannes:

[math] p'(x)= C \cdot w(x) [/math]

(4.14)

hvor C er en proporsjonalitetskonstant og p’ er trykket pr. enhetsflate pr. halve sville.

Differensiallikningen beskriver forholdet pr. enhetslengde for den langsgående akse til skinnen. I en overbygning med sviller på tvers av sporets lengdeakse postulerte derfor Winkler følgende relasjon:

[math] p(x)= b \cdot p'(x,y)= b \cdot C \cdot w(x) [/math]

(4.15)

b er bredden av en tenkt langsvilleoverbygning.

Den endelige differensiallikningen kan derfor uttrykkes slik:

[math] E \cdot I_{X-X} \cdot \left( { d^4 w \over dx^4 } \right) b \cdot C \cdot w(x) = q(x) [/math]

(4.16)

Anvendelse av denne teorien medfører at overbygningens tverrsvillesystem må omvandles til en langsvilleoverbygning. Dette skal belyses nærmere i etterfølgende kapitler.

Det er allerede i innledningen pekt på at skinnen skal fungere som bærebjelke og som kjøreveg.

Mht. skinnen som bærebjelke skal i det etterfølgende beskrives en metode med utgangspunkt i grunnligningen for bøyelinjen til en bjelke som er opplagret kontinuerlig på et jevnt elastisk underlag, for dimensjonering av overbygningen. Metoden kalles "Zimmermanns metode" og den ble undersøkt ved det tekniske universitetet i München i Tyskland ved "Institut für Eisenbahnbau und Strassenbau" på oppdrag fra de tyske forbundsbaner. I avhengighet av forskjellige parametre muliggjør metoden beregning av spenninger i skinnen og deformasjoner (nedsenking) av skinnen ved passering av det rullende materiell. Dimensjoneringsmetoden er et meget nyttig verktøy for bestemmelse av tillatte aksellaster som funksjon av sporets tilstand. I forbindelse med den teoretiske verifisering av "Zimmermanns metode" ble det gjennomført omfangsrike forsøk. Disse forsøkene bekrefter den anvendte teori ut fra tilgjengelige overbygningskonstruksjoner og rullende materiell på 1950 - tallet da modellen var gjenstand for stor oppmerksomhet ved tyske tekniske universitet.

Siden den gang har det vært en stor utvikling av overbygningskonstruksjoner og av det rullende materiell. Men modellen er fremdeles vel egnet til dimensjonering av overbygningen for hastigheter opp til 200 km/h og skulle derfor kunne finne anvendelse ved JBV.

5.2 Grunnleggende teori

Beregningsmetoden for fastsettelse av de totale krefter settes sammen av:

• Zimmermanns metode

• Eisenmanns metode

Zimmermannutviklet en metode for beregning av de ytre kvasistatiske belastninger forårsaket av det rullende materiell når det står stille i sporet eller framføres med lav hastighet. Omlagring av hjullastene på grunn av sentrifugalkraftensom dog er hastighetsavhengig, inngår i begrepet kvasistatisk belastning. Sporet betraktes som en kontinuerlig bjelke som hviler på et elastisk underlag.

Eisenmann bygget på metoden til Zimmermann og utviklet en modell for beregning av de dynamiske belastninger som oppstår ved framføring av det rullende materiell.

De kvasistatiske og dynamiske belastningene adderes og summen gir den totale belastning. Denne belastningen gir grunnlaget for beregning av bøyemomenter og spenninger i skinnene samt den såkalte støttepunktkraften S som betongsvillen må dimensjoneres for. Støttepunktkraftens angrepspunkt er i skinneleiene.

Utgangspunktet er som nevnt at sporet betraktes som en kontinuerlig bjelke som hviler på et elastisk underlag med gitt stivhet. Avhengig av elastisitetsforholdene i sporet vil hjulkreftene fordele seg over flere sviller. Betongsvillene plasseres på tvers i sporets lengderetning og svillene med skinner danner således et tverrsvillespor. I utviklingen av beregningsmetoden forutsetter Zimmermannat dette tverrsvillesporet gjøres om til et langsvillespor.

Metoden er dermed en tilnærmet modell av virkeligheten da skinnene har opplager i diskrete opplegg gjennom svillene. Men på grunn av krav til større aksellaster og høyere hastigheter stilles det strengere krav til overbygningen. Dette medfører bl.a. at svillene må legges med mindre svilleavstand. Med senteravstand lik 600 mm kan overbygningskonstruksjonen med god nøyaktighet betraktes som en langsvilleoverbygning.

Forutsetningene i den matematiske modell er:

• Sporet betraktes som en uendelig lang bjelke som er opplagret på et homogent og jevnt elastisk underlag

• Den uendelig lange bjelke er vektløs

• Den uendelige lange bjelke er fast forbundet med det elastiske underlaget

Det kreves 2 betingelser som settes lik hverandre (likevektsbetingelse):

• Deformasjon av det elastiske underlaget ved belastning med enkeltlast

• Nedbøyning av den uendelige lange bjelke som hviler på det elastiske underlaget

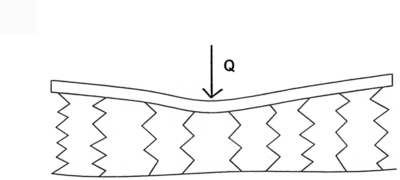
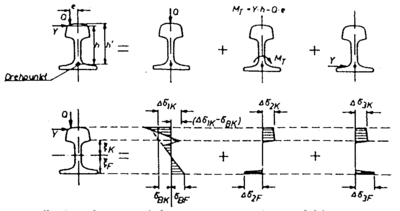
Det vises til figur 4.11.

Figur Figur 4.11 Likevektsbetingelse i Zimmermanns metode tilsier at deformasjonen av det elastiske underlaget ved belastning med enkeltlast er i likevekt med nedbøyningen av den uendelige lange bjelke som hviler på det elastiske underlaget.

5.2.1 Deformasjon av det elastiske underlaget ved enkeltlast Q

Utgangspunktet er Winklers hypotese om at trykket i det elastiske underlaget fra belastningen er proporsjonal med deformasjonen:

[math] \sigma (x) = C \cdot y(x) [/math]

(4.17)

C er proporsjonalitetskonstanten som uttrykker fjærstivheten i det elastiske underlaget.

y(x) er deformasjonen i det elastiske underlaget ved stedet x.

s(x) er trykket i det elastiske underlaget ved stedet x.

Det vises til figur 4.12.

Figur 4.12 Winklers hypotese om at trykket i det elastiske underlaget er proporsjonalt med deformasjonen.

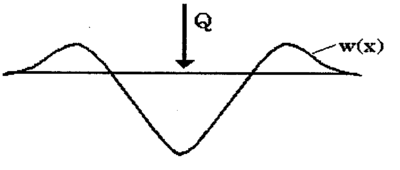
Det defineres en bredde b til den uendelige lange bjelke. Det forutsettes videre symmetrisk fordeling av belastningen på det elastiske underlaget for bøyelinje og momentforløp på grunn av enkeltlasten Q. Det vises til figur 4.13.

Figur 4.13 Symmetrisk deformasjonslinje til det elastiske underlaget om enkeltlast Q.

Det er dermed tilstrekkelig å betrakte den ene halvdelen av den uendelige lange bjelke mht. bøyelinje og momentlinje om enkeltlasten Q.

Dette medfører:

[math] {Q \over 2} = \int_0^ \infty \sigma (x) \cdot bdx = \int_0^ \infty C \cdot y(x) \cdot bdx [/math]

(4.18)

Det er ønskelig å betrakte stedet x for å kunne utlede en generell beskrivelse:

[math] {Q \over 2} = \int_0^ X C \cdot y(x) \cdot bdx + \int_X^ \infty C \cdot y(x) \cdot bdx [/math]

(4.19)

Skjærkraften ved stedet x kan dermed utledes:

[math] Q(x) = \int_X^ \infty C \cdot y(x) \cdot bdx = {Q \over 2} - \int_0^ X C \cdot y(x) \cdot dx [/math]

(4.20)

[math] Q(x) = {Q \over 2} - C \cdot b\int_0^ X y(x) dx [/math]

(4.21)

Forandring av skjærkraften over en lengdeenhet dx kan beregnes ved derivasjon:

[math] {dQ \over dx} = C \cdot b \cdot y(x) [/math]

(4.22)

5.2.2 Deformasjon av den uendelige lange bjelke

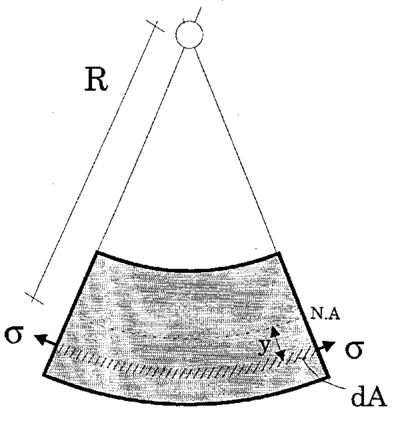
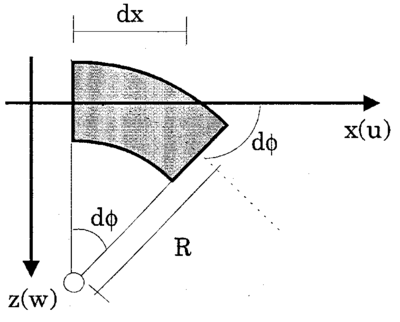
Den uendelige lange bjelke som er opplagret på det elastiske underlagt, blir utsatt for bøyning. Under forutsetning av at nøytralaksen faller sammen med arealaksen i krummningsforløpet, gjelder iht. anerkjente teorier i fasthetslæren:

[math] y '' = - {1 \over R} = - {M \over EI} [/math]

(4.23)

Dette gir:

[math] {d^2 y \over dx^2} = - {M \over EI} [/math]

(4.24)

y er deformasjonen av bjelken langs lengdeaksen x.

EI er stivheten til bjelken uttrykt som produktet av elastisitetsmodulen E (N/mm²) og treghetsmomentet I(mm⁴). Det vises til figur 4.14.

Figur 4.14 Krummningsforløpet til en bjelke med stivhet lik EI.

Ovenstående likning kan omskrives og løses mht. momentet:

[math] M = -E \cdot I \cdot {d^2 y \over dx^2} [/math]

(4.25)

Skjærkraften framkommer ved derivasjon:

[math] Q = {dM \over dx} = -E \cdot I \cdot {d^2 y \over dx^2} [/math]

(4.26)

Ved å derivere skjærkraften framkommer deformasjonen av bjelken:

[math] {dQ \over dx} = -E \cdot I \cdot {d^4 y \over dx^4} [/math]

(4.27)

5.2.3 Etablering av likevektsbetingelse

I dette avsnittet blir bøyelinjen og momentlinjen for den uendelig lange bjelke på det elastiske underlaget utledet.

De 2 uttrykkene for variasjon av skjærkraften over en lengdeenhet dx settes lik hverandre på grunn av betingelse for likevekt:

[math] {dQ \over dx} = C \cdot b \cdot y(x) = -E \cdot I \cdot {d^4 y \over dx^4} [/math]

(4.28)

Uttrykket til venstre for likhetstegnet er deformasjonen av det elastiske underlaget. Uttrykket til høyre beskriver nedbøyningen av den uendelige lange bjelke på det elastiske underlaget.

Det ble gjort den antakelse om at den uendelige lange bjelke hele tiden er fast forbundet med det elastiske underlaget.

Likevektsbetingelsen gir følgende differensiallikning av 4. grad:

[math] C \cdot b \cdot y(x) = -E \cdot I \cdot {d^4 y \over dx^4} [/math]

(4.29)

[math] C \cdot b \cdot y(x) \cdot { 1 \over E \cdot I} + {d^4 y \over dx^4} = 0 [/math]

(4.31)

Denne likningen er utgangspunktet for Zimmermanns metode. Den uttrykker hvordan den uendelige lange bjelke deformerer seg når den hviler på et elastisk underlag med jevn og homogen elastisitet. Det ideelle spor arbeider etter denne differensiallikningen.

Differensiallikningen har følgende randbetingelser:

[math] y( \infty ) = 0 [/math]

(4.32)

[math] y( 0 ) = 0 [/math]

(4.33)

[math] y'''( 0 ) = { Q \over 2 \cdot E \cdot I } [/math]

(4.34)

Med omskrivning gjelder:

[math] -C \cdot b \cdot y = E I \cdot {d^4 y \over dx^4} [/math]

(4.35)

[math] - y = {E I \over Cb} \cdot {d^4 y \over dx^4} [/math]

(4.36)

[math] - 4y = {4E I \over Cb} \cdot {d^4 y \over dx^4} [/math]

(4.37)

For den videre utledning er det hensiktsmessig å innføre nye begreper:

[math] L = \sqrt [4] { 4EI \over Cb} [/math]

(4.38)

dvs.

[math] L^4 = { 4EI \over Cb} [/math]

(4.39)

og

[math] {x \over L} = \xi \ \ \ og \ \ \ {dx \over L} = d \xi \ \ \ \rArr \ \ \ { d^4 x \over L^4} = d \xi^4 [/math]

(4.40)

Dette medfører:

[math] - 4y = L^4 \cdot {d^4 y \over dx^4} = L^4 \cdot {d^4 y \over L^4 \cdot d \xi^4} [/math]

(4.41)

Dette gir:

[math] - 4y = {d^4 y \over d \xi^4} [/math]

(4.42)

Det skal vises at denne differensiallikningen har løsningen:

[math] y = K \cdot { \sin \xi + \cos \xi \over e^\xi} [/math]

(4.43)

hvor

[math] \eta = { \sin \xi + \cos \xi \over e^\xi} [/math]

(4.44)

dvs.

[math] y = K \cdot \eta [/math]

(4.45)

Koeffisienten K må bestemmes.

Ovennevnte uttrykk kan beskrives generelt:

[math] f(x) \over g(x) [/math]

(4.46)

Den deriverte av en funksjonsbrøk er gitt ved uttrykket:

[math] {d \over dx} \left( { f(x) \over g(x)} \right) = { f'(x) \cdot g(x) - g'(x) \cdot f(x) \over g(x)^2} [/math]

(4.47)

Det er også kjent fra matematikken at den deriverte av en sum av 2 funksjoner er gitt ved:

[math] {d \over dx} (f(x) \plusmn g(x)) = {d \over dx} f(x) \plusmn {d \over dx} g(x] [/math]

(4.48)

hvor funksjonen er definert ved:

[math] f(x) \plusmn g(x) [/math]

(4.49)

Den 1. deriverte blir:

[math] y' = K \cdot \left( { ( cos \xi - sin \xi) \cdot e^\xi - (sin \xi + cos \xi ) \cdot e^\xi \over e^{2 \xi}} \right) [/math]

(4.50)

[math] y' = -2K \cdot {sin \ \xi \over e^\xi} [/math]

(4.51)

Av denne funksjonen utledes den 2. deriverte:

[math] y'' = -2K \cdot{ cos \xi \cdot e^\xi - sin \xi \cdot e^\xi \over e^{2 \xi}} [/math]

(4.52)

[math] y'' = 2K \cdot{ cos \xi - sin \xi \over e^{ \xi}} [/math]

(4.53)

Den 3. deriverte kan også utledes:

[math] y''' = 2K \cdot { ( cos \xi + sin \xi) \cdot e^\xi - (sin \xi - cos \xi ) \cdot e^\xi \over e^{2 \xi}} [/math]

(4.54)

[math] y''' = 4K \cdot { cos \xi \over e^\xi} [/math]

(4.55)

Endelig blir den 4. deriverte:

[math] y'' \ '' = 4K \cdot {-sin \xi \cdot e^\xi - cos \xi \cdot e^\xi \over e^{2 \xi}} [/math]

(4.56)

[math] y'' \ '' = -4K \cdot {sin \xi + cos \xi \over e^{ \xi}} [/math]

(4.57)

Vi ser at antakelsen er bevist:

[math] {d^4 y \over dx^4} = y'' \ '' = -4 \cdot y [/math]

(4.58)

Det er allerede innført hjelpefunksjonen:

[math] dx = L \cdot d \xi [/math]

(4.59)

På grunn av symmetri om enkeltlasten Q₀ gjelder som allerede nevnt følgende likevektsbetingelse:

[math] {Q_0 \over 2 } = b \cdot C \cdot \int_0^ \infty ydx [/math]

(4.60)

[math] {Q_0 \over 2 } = b \cdot C \cdot L \cdot \int_0^ \infty yd \xi [/math]

(4.61)

Det er allerede definert:

[math] y = K \cdot \eta [/math]

(4.62)

hvor

Dette gir:

[math] {Q_0 \over 2 \cdot b \cdot C \cdot L} = \int_0^ \infty K \cdot \eta d \xi = K \cdot \int_0^\infty \eta d \xi [/math]

(4.63)

Integralet skal løses ved delvis integrasjon:

[math] K \cdot \int_0^ \infty \eta d \xi = K \int_0^ \infty e^{-X} \cdot (sin(x) + cos(x)) dx [/math]

(4.64)

I matematikken er gitt regler for derivasjon av et produkt:

[math] {d \over dx} (f(x) \cdot g(x)) = g(x) \cdot {d \over dx} f(x) + f(x) \cdot {d \over dx}g(x) [/math]

(4.65)

Hvert ledd integreres:

[math] \int {d \over dx} (f(x) \cdot g(x)) = \int g(x) \cdot {d \over dx} f(x) + \int f(x) \cdot {d \over dx} g (x) [/math]

(4.66)

Regelen for delvis integrasjon benyttes:

[math] \int g(x) \cdot {d \over dx} f(x) = f(x) \cdot g(x) - \int f(x) \cdot {d \over dx} g (x) [/math]

(4.67)

Ved hjelp av denne regelen kan integralet løses:

[math] I = \int_0^ \infty e^{-X} \cdot (cos(x) + sin(x))dx [/math]

(4.68)

[math] I = \left[ -e^{-X} \cdot (cos(x) + sin(x)) \right]_0^ \infty - \int_0^ \infty -e^{-X} \cdot (-sin(x) + cos(x))dx [/math]

(4.69)

[math] I = 1+\int_0^ \infty e^{-X} \cdot (cos(x) - sin(x))=1+J [/math]

(4.70)

[math] J = \left[ -e^{-X} \cdot (cos(x) - sin(x)) \right]_0^ \infty - \int_0^ \infty -e^{-X} \cdot (-sin(x) - cos(x))dx [/math]

(4.71)

[math] J = 1-I [/math]

(4.72)

[math] I=1+1-I [/math]

(4.73)

[math] I=1 [/math]

(4.74)

Det er utledet:

[math] \int_0^ \infty { sin(x) + cos(x) \over e^X} dx = 1 [/math]

(4.75)

Altså gjelder også:

[math] \int_0^ \infty \eta d \xi = 1 [/math]

(4.76)

Følgende matematiske relasjon må gjelde:

[math] {Q_0 \over 2 \cdot b \cdot C \cdot L} = K \cdot \int_0^ \infty \eta d \xi = K \cdot 1 = K[/math]

(4.77)

[math] y = K \cdot \eta [/math]

(4.78)

Likningen for bøyelinjen blir:

[math] y = {Q_0 \over 2bCL} \cdot \eta [/math]

(4.79)

hvor

[math] \eta = { sin \xi +cos \xi \over e^ \xi} [/math]

(4.80)

Med relasjonen

[math] \xi = { x \over L} [/math]

(4.81)

blir likningen for bøyelinjen:

[math] y = {Q_0 \over 2bCL} \cdot e^{-{ \left \vert X \right \vert \over L}} \cdot ( cos \left( { \left \vert X \right \vert \over L} \right) + sin \left( { \left \vert X \right \vert \over L} \right) )[/math]

(4.82)

Bøyemomentets linje skal defineres:

[math] M = f(x)=EI \cdot \left( - { d^2 y \over dx^2} \right) [/math]

(4.83)

[math] { d^2 y \over dx^2} = 2K \cdot { sin \xi - cos \xi \over e^\xi} = 2K \cdot (- \mu ) [/math]

(4.84)

[math] { d^2 y \over dx^2} = { d^2 y \over d \xi^2} \cdot {1 \over L^2} = {2K \over L^2} \cdot ( - \mu ) [/math]

(4.85)

Det er allerede blitt definert:

[math] K= { Q_0 \over 2bCL} [/math]

(4.86)

[math] L^4 = {4EI \over bC} [/math]

(4.87)

Dette gir:

[math] M={Q_0 \cdot L \over 4} \cdot \mu [/math]

(4.88)

[math] \mu ={sin \xi -cos \xi \over e^\xi} [/math]

(4.89)

Dermed er utledet likningen for bøyelinjen:

[math] y(x)={Q \over 2 \cdot b \cdot C \cdot L} \cdot e^{-{ \left \vert X \right \vert \over L}} \cdot (cos \left( { \left \vert X \right \vert \over L} \right)+ sin \left( { \left \vert X \right \vert \over L} \right) ) [/math]

(4.90)

og tilsvarende likningen for bøyemomentet:

[math] M(x)={Q \cdot L \over 4} \cdot e^{-{ \left \vert X \right \vert \over L}} \cdot (sin \left( { \left \vert X \right \vert \over L} \right)- cos \left( { \left \vert X \right \vert \over L} \right) ) [/math]

(4.91)

5.3 Dimensjonerende forutsetninger

Med utgangspunkt i den nominelle aksellast P er det mulig med "Zimmermanns metode" å beregne :

• Bøyemoment i skinnen (skinnen fungerer som bærebjelke)
• Bøyespenningen i u.k. av skinne midt på skinnefoten
• Deformasjon (nedsenking) av skinnen
• Støttepunktkraftensom er den kraft som betongsvillendimensjoneres for

Ved behov kan naturligvis bøyespenninger på andre steder på skinneprofilet beregnes dersom tilsvarende treghetsmoment, evt. motstandsmoment er kjent.

Det gjøres følgende forutsetninger:

• Utgangspunktet er den kvasistatiske hjulkraft Q_{KV. STAT.} Dette betyr at dimensjoneringen foregår i kvasistatisk tilstand. Med kvasistatisk tilstand menes at det rullende materiellet er stillestående
• Det forutsettes at Q_{KV. STAT.} angriper sentrisk i skinnehodet
• Det tas ikke hensyn til langsgående krefter
• Normalt tas det ikke hensyn til laterale (horisontale) krefter
• Det forutsettes en ballasttykkelse på 300 mm under u.k. sville
• Det forutsettes belastningstrykk mot svillen som for nyjustert spor

5.4 Dimensjonerende parametre

Viktige parametre for dimensjoneringen av overbygningen er:

• Skinnens dvs. stålets elastisitetsmodul

• Skinneprofilets treghetsmoment

• Svillens (dvs. betongsville) flate

• Avstand mellom svillene

• Undergrunnens beskaffenhet (fjell, morene, leire etc.)

5.5 Beskrivelse av modellen

Iht. grunnligningen for bøyelinjen til en kontinuerlig opplagret bjelke på jevnt elastisk underlag tenkes skinnen opplagret på et fjærsystem som vist i figur 4.15. Denne modellen er utgangspunktet for dimensjoneringsmetoden til Zimmermann. Metoden muliggjør beregning av middelverdier av spenninger og nedsenking av skinnen i kvasistatisk tilstand. De beregnede middelverdier stemmer godt overens med måleverdi er som er fremkommet ved omfangsrike forsøk i sporet. Det forutsettes kjennskap til skinnens stivhet uttrykt ved elastisitetsmodulen E og treghetsmomentet I_XX og til fjærbetingelsene for skinnens opplagring. Videre representerer modellen en ideell tilstand med konstant kontinuerlig og elastisk opplagring av skinnen. Men med grunnlag i denne modellen kan det ikke gjøres noen utsagn over spredningen av måleverdiene.

4.15 Teoretisk modell for dimensjonering av overbygningen. Modellen muliggjør beregning av middelverdier av spenninger i skinnen og nedsenking av skinnen i kvasistatisk tilstand.

I figur 4.16er vist en modell som tar hensyn til den virkelige tilstanden i sporet. Det fremgår at skinnen er opplagret uregelmessig og at sporets elastisitet derved er variabel. Dette har sammenheng med at fjærbetingelsene for opplagringen av skinnen forandrer seg og at denne opplagringen på det faste underlaget dvs. undergrunnen varierer. Som funksjon av hastigheten og uregelmessigheter på skinnehodet samt på hjulene til det rullende materieller det mulig å beregne spredningene dvs. de maksimale og minimale verdier av skinnespenninger og nedsenking av skinnen i dynamisk tilstand. Utgangspunktet er Zimmermanns metode.

Det forutsettes dermed en kontinuerlig elastisk opplagring av skinnen hvor elastisiteten er variabel. Varierende elastisitet skyldes at det i ballasten er hulrom som opptrer i forskjellige størrelser i det vesentligste under svillen. Dette har sin årsak i pukkens geometriske form. Skinnens stivhet er konstant.

Figur 4.16 Modell som viser den virkelige tilstand i sporet. Modellen tar utgangspunkt i variabel elastisitet i sporet og uregelmessigheter i o.k. skinne og i hjul. Skinnens stivhet forutsettes konstant. Ved anvendelse av Zimmermanns metode muliggjør modellen beregning av minste og største verdier av spenninger i skinnen og nedsenking av skinnen.

5.6 Ballastsifferet

Vesentlig for den anvendte teori er introduksjonen av ballastsifferet C (N/mm³) som beskriver undergrunnens beskaffenhet og hvordan ballastlaget gir etter for undergrunnens egenskaper ved belastning fra det rullende materiell. Ballastsifferet kan derfor variere mht. til hvilket materiale undergrunnen består av og også mht. årstiden.

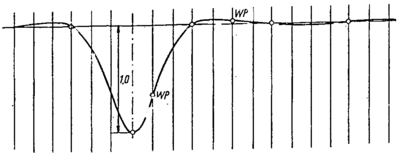
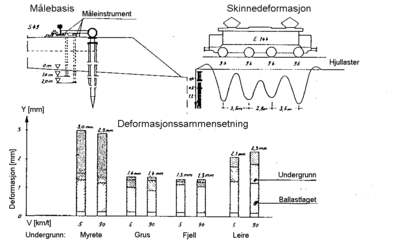
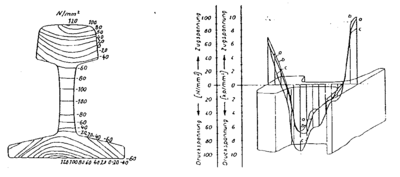
I figur 4.17 er anskueliggjort måleresultatene av nedsenkingen under et tysk lokomotiv (E 144) ved forskjellige undergrunnsarter som:

• myr
• leire
• grus
• fjell

Det er i forsøksserien forutsatt en ballasttykkelse på 30 cm under u.k. av svillen.

Figur 4.17 Bildet viser målinger avnedsenkingen av skinnen under det tyske lokomotivet E 144 ved forskjellige typer undergrunn. Tykkelsen av ballasten under u.k. av sville er i alle tilfellene 300 mm.

Det er meget interessant å legge merke til at nedsenkingen av skinnen i ballastlaget under lokomotivet er tilnærmet den samme for alle typer undergrunn.

Nedsenkingen av ballastlaget i undergrunnen varierer derimot meget. Ved bløt undergrunner nedsenkingen vesentlig større enn ved f.eks. undergrunn av fjell. Undergrunnen får også en nedsenking på grunn av ovenforliggende masser. Dette gjør seg spesielt gjeldende ved bløte masser. I det omtalte forsøket ovenfor ble det registrert nedsenking av myrete undergrunn i en dybde av 3 m under o.k. skinnehode.

Ballastsifferet kan også få varierende verdier avhengig av årstiden og ved økende belastning. Denne forandringen forårsakes av værforhold som frost og regn samt at de enkelte korn omlagres og knuses over tid på grunn av belastningen. Om vinteren kan både ballastlaget og enkelte typer jordarter i undergrunnen bli utsatt for frost. Dette fører til forandring av ballastsifferet. I Tabell 4.1er angitt den typiske forandring av ballastsifferet gjennom året. Figuren viser at under forutsetning av ballastrenset spor i oktober antar ballastsifferet en høyere verdi i november etter at 0,5 x 10⁶ tonn har passert over sporet. I desember inntreffer frost som medfører enda en økning av ballastsifferet etter at 1,0 x 10⁶ tonn har passert. I mars etterfølgende år har frosten forsvunnet og ballastlaget med undergrunnen er blitt bløtere. Dette fører til en lavere verdi for ballastsifferet. Utover sommeren synker ballastsifferet og i november antar C sin laveste verdi på grunn av mye nedbør. årsaken til den lave verdien er sannsynligvis manglende drenering.

Tabell 4.1 Tabellen angir variasjonen av ballastsifferet(Bettungszahl) gjennom årstiden. F.eks. antar ballastsifferet en høyere verdi ved frost enn i en periode med rikelig nedbør. Videre er angitt nedsenkingen av sporet. Tallene i parentes er innerstreng i en kurve.

	Nedsenking			Ballastmodul
Målinger etter a x 106 tonn ved passering (måned)	Middelverdi med mer	Standardavvik med mer	Skjevhet mm	Middelverdi N/mm3	Standardavvik N/mm3	Skjevhet N/mm3
Justering av sporet i oktober	0.08 (0.10)	0.11 (0.12)	1.46 (1.67)	0.132	0.026	0.010
a = 0,5 november	0.09 (0.07)	0.13 (0.12)	2.55 (1.97)	0.184	0.050	0.014
a = 1,0 desember (frost)	0.12 (0.15)	0.14 (0.19)	2.31 (2.23)	0.202	0.054	0.020
a = 3,3 mars (frost forsvinner)	0.09 (0.15)	0.19 (0.23)	3.30 (1.85)	0.140	0.046	0.060
a = 5,5 juli	0.16 (0.17)	0.20 (0.27)	3.27 (2.35)	0.145	0.043	0.060
a = 8,3 november	0.11 (0.13)	0.22 (0.21)	3.84 (2.58)	0.117	0.027	0.015

Ballastsifferet antar altså forskjellige verdier. Det kan variere i området fra 0,01 - 0,4 N/mm³ . I ekstreme tilfeller kan C bli enda høyere, helt opp til 0,5 N/mm³. Lav C betyr bløt undergrunnog høy C betyr hard undergrunn. Nedenfor er listet opp noen eksempler :

* C < 0,05 N/mm3	meget bløt undergrunnf. eks. myrete
* 0,05 < C < 0,15 N/mm3	fra bløt til fast leire
* 0,15 < C < 0,30 N/mm3	fast leiretil grus
* C > 0,30 N/mm3	fjell(også fjellskjæring)

Ballastsifferet er en meget viktig parameter som utøver betydelig innflytelse på de faktiske forhold i sporet og også på resultatet av dimensjoneringen ved belastning. Det er derfor meget viktig å fastsette riktig verdi av C ved å studere undergrunnen. Ballastsifferet lar seg selvfølgelig også bestemme ved eksperimentelle forsøk.

Ballastsifferet beskrives på følgende måte :

[math] C= tg \beta = {p \over y} [N/mm^3] [/math]

(4.92)

hvor

• p = ballasttrykketved belastning fra det rullende materiell [N/mm²]
• y = nedsenking av skinnen [mm]

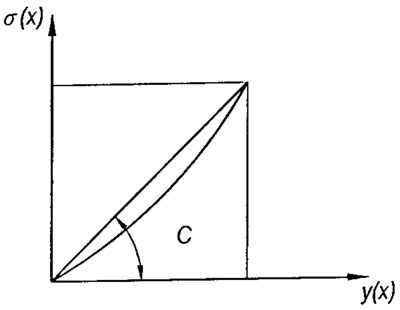
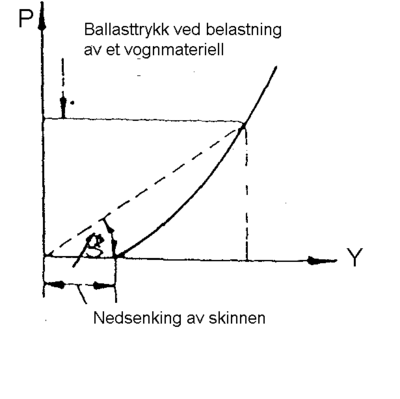
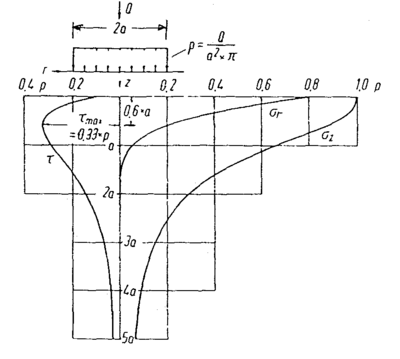
I figur 4.18 er C vist som vinkelkoeffisienten i et p/y - aksesystem. Det er verdt å legge merke til at ballasttrykket i sin helhet først blir virksom etter litt nedsenking av svillen, vesentlig på grunn av hulrom under sville.

Figur 4.18 Bildet angir sammenhengen mellom ballasttrykket ved belastning av et vognmateriell og nedsenking av skinnen.

Ballastsifferet er vinkelkoeffisienten i koordinatsystemet. Med utgangspunkt i figur 4.18kan den statiske stivheten eller ballastsifferet i det lineære området til fjærlinjen beregnes etter følgende formel:

[math] C_{STAT.} = {P \over y \cdot A} [N/mm^3] [/math]

(4.93)

Her betyr:

• P er trykkraften [N]
• A er den medvirkende lastflate [mm²]
• y er nedsenkingen [mm]

I det ikke lineære området må det benyttes en differensiell betraktningsmåte:

[math] C_{STAT.} = { \Delta P \over \Delta y \cdot A} [/math]

(4.94)

5.6.1 Beregning av det resulterende ballastsifferet

I nyere overbygningskonstruksjoner har mellomleggsplaten mellom skinne og sville gjennomgått forbedringer mht. evnen til å redusere spissbelastningene ved passering av det rullende materiell. For eksempel har mellomleggsplaten i 10 mm gummi i knottet utførelse en sterkt forbedret evne til å ta opp støtbelastningene enn den eldre mellomleggsplaten 5 mm EVA. Begge mellomleggsplater er i bruk ved Jernbaneverket i dag.

Det er av betydning å kunne bestemme den dynamisk virksomme stivhet til den elastiske mellomleggsplaten. Iht. studier gjort i regi av ERRIi ” Study of chatacteristics of rail fastening systems – final recommendations for test methodes, ERRI D 170/RP 5 mars 1994” er vibrasjonene i lavfrekvente områder bestemmende. I rapporten anbefales å multiplisere den statiske stivhet med en faktor lik 1,5. Dette betyr at den dynamisk virksomme stivhet til Pandrol10 mm mellomleggsplate i gummi i knottet utførelse for det rullende materiell kan settes lik:

[math] c_{PANDROL \ GUMMI \ 10MM} = 1,5 \cdot 45 = 70kN/mm [/math]

(4.95)

Til sammenligning er den tilsvarende dynamisk virksomme stivheten til PANDROL EVA5 mm plast lik:

[math] c_{PANDROL \ EVA \ PLAST} = 700kN/mm [/math]

(4.96)

Til sammenligning har den nye mellomleggsplaten til Vosslohsom benyttes på høyhastighetsbanene på konvensjonelt spor i Tyskland, en dynamisk fjærstivhetlik:

[math] c_{VOSSLOH} = 100kN/mm [/math]

(4.97)

Denne mellomleggsplaten er altså noe stivere enn mellomleggsplaten til Pandrol.

Det skal beregnes den resulterende stivhet og det resulterende ballastsiffer til overbygningskonstruksjonen under medvirkning av en høyelastisk mellomleggsplate i skinnebefestigelsen.

Med utgangspunkt i ballastsifferet C_BALLAST til overbygningen kan ballastlagets fjærstivhet beregnes uten å ta hensyn til mellomleggsplatens stivhet:

[math] c_{BALLAST} = C_{BALLAST} \cdot {F \over 2} \ (kN/mm) [/math]

(4.98)

F er svillens belastede flate i mm². Denne flaten blir beregnet i neste avsnitt.

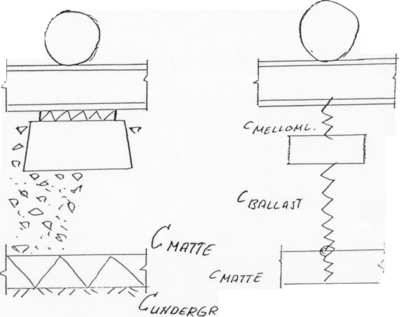
Overbygningskonstruksjonens resulterende stivhet c_RES. (kN/mm) under medvirkning av en høyelastisk mellomleggsplate kan beregnes. De 2 elastiske lagene – mellomleggsplaten og ballasten– kan tenkes koblet etter hverandre i en kjede. Det vises til figur 4.19.

Figur 4.19 Prinsipp for seriekobling av fjærer.

Under forutsetning av udempede og frie vibrasjoneran gir litteraturen den resulterende stivhet for overbygningskonstruksjonen til å være:

[math] { 1 \over c_{RES.}} = { 1 \over C_{BALLAST}} + { 1 \over C_{MELLOMLEGGSPLATE}} [/math]

(4.99)

Vibrasjonene ved passering av et rullende hjul er ikke udempede iht. den strenge teori på grunn av mellomleggsplatens materiale som er gummi. Gummi demper vibrasjonene. Imidlertid bekrefter forsøk for ICE-tog i Tyskland at ovenstående formel kan benyttes med stor grad av nøyaktighet.

Den resulterende stivhet til overbygningskonstruksjonen kan omskrives til:

[math] c_{RES.} = { c_{MELLOMLEGGSPLATE} \cdot c_{BALLAST} \over c_{MELLOMLEGGSPLATE} + c_{BALLAST} } [/math]

(4.100)

I ovenstående formel må den dynamiske stivheten til mellomleggsplaten benyttes. For ballasten gjelder den statiske verdi.

Overbygningskonstruksjonens resulterende ballastsiffer kan dermed beregnes:

[math] c_{RES.} = { c_{RES.} \over {F \over2} } = 2 \cdot {c_{RES.} \over F} [N/mm^3] [/math]

(4.101)

Mellomleggsplatens karakteristiske egenskaper får dermed betydning. Spesielt ved hard undergrunn med C_BALLAST> 0,30 -–0,40 N/mm³ blir overbygningskonstruksjonen mykere med et resulterende ballastsiffer som er betydelig mindre enn ballastens ballastsiffer ved bruk av 10 mm mellomleggsplate i gummi i knottet utførelse.

EVA Pandrol plast 5 mm med dynamisk virkende stivhet lik 700 kN/mm har nesten ingen betydning for det resulterende ballastsiffer til overbygningskonstruksjonen. Ved bruk av denne mellomleggsplaten blir i praksis:

[math] C_{RES.} = C_{BALLAST} [/math]

(4.102)

5.6.2 Eksempel på beregning av resulterende ballastsiffer

Det skal vises ved et eksempel hvordan det resulterende ballastsiffer beregnes for en overbygningskonstruksjon med høyelastisk mellomleggsplate av type Pandrol10 mm i gummi i knottet utførelse og med ballast med tykkelse 300 mm under u.k. sville lagt på hardt underlag.

Det tas utgangspunkt i kjent teori i litteraturen med seriekobling av fjærstivheter. Kjente parametre er:

• c_{MELLOMLEGGSPLATE} = 70 kN/mm
• C_BALLAST = 0,40 N/mm³
• F = 570.000 mm²

Ballastens stivhet over belastet flate beregnes:

[math] c_{BALLAST} = {C_{BALLAST} \over {F \over 2 } } = { 0.40 \over{570000 \over 2}} \cdot 10^{-3} = 114 kN/mm [/math]

(4.103)

Overbygningskonstruksjonens resulterende stivhet beregnes:

[math] c_{RES.} = { c_{MELLOMLEGGSPLATE} \cdot c_{BALLAST} \over c_{MELLOMLEGGSPLATE} + c_{BALLAST} } [/math]

(4.104)

[math] c_{RES.} = { 70 \cdot 114 \over 70 + 114 } = 43.4 kN/mm [/math]

(4.105)

Dette gir følgende resulterende ballastsiffer:

[math] C_{RES.} = {c_{RES.} \over {F \over 2 } } = { 43.4 \over{570000 \over 2}} \cdot 10^{-3} = 0.15 kN/mm^3 [/math]

(4.106)

Overbygningskonstruksjonen er blitt vesentlig mykere. Derav følger også at nedsenkingen av skinnen og bøyepåkjenningen på skinnen er blitt større. Men med et ballastsiffer på 0.15 N/mm³ er det ingen fare for at grenseverdier mht. disse parametrene blir overskredet. Grenseverdiene er påkrevet for å sikre god kjøredynamikk og tilfredsstillende sporstabilitet samt at skinnespenningeneikke skal komme opp på et nivå som tilsvarer spenningene i utmattingstilstanden.

5.7 Langsvilleoverbygning

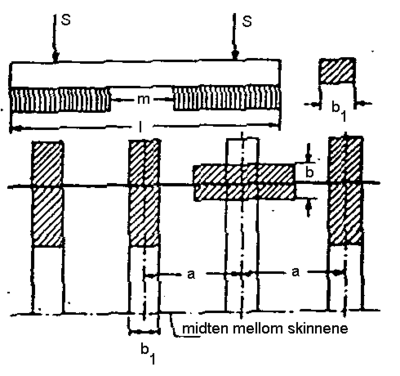
Dimensjoneringsmetoden forutsetter at tverrsvilleoverbygningen (svillene er lagt på tvers av skinnestrengen) gjøres om til en langsvilleoverbygning med tenkt bredde b. Med dette menes et tenkt system hvor svillene er lagt langs med skinnestrengen og at dette systemet har samme lastflate som svillenes lastflate i en tverrsvilleoverbygning. Videre forutsettes at skinnen da blir kontinuerlig opplagret på det tenkte systemet. Det vises til figur 15. Det antas at midtre del av betongsvillener opplagerfri. Forholdet tilsvarer et nyjustert spor.

Følgende betegnelser innføres :

• F = Belastet opplagerflate til svillen (mm²)
• l = Svillens lengde (mm)
• m = Lengde av ubelastet midtdel av svillen (mm)
• a = Svilleavstand (mm)
• b₁= Svillens bredde (mm)
• b = Bredde av tenkt langsvilleoverbygning (mm)

Med ovennevnte betegnelser blir den belastede opplagerflate til betongsvillen:

[math] F=(l-m) \cdot b_1 [mm^2] [/math]

(4.107)

Den tenkte bredde av langsvillen blir da :

[math] b={F \over (2 \cdot a)} [mm] [/math]

(4.108)

Figur 4.20 Beregning av belastet flate i en tenkt langsvilleoverbygning.

5.8 Beregning av grunnverdi L

For den videre dimensjonering er det nødvendig å innføre følgende parametre:

• I_X-X = Skinneprofilets treghetsmomentom den sterke akse (mm⁴)
• E = Elastisitetsmodulen til skinnestålet (N/mm²)
• C_RES. = Resulterende ballastsiffer (N/mm³)
• b = Bredde i langsvilleoverbygning (mm)

Med disse parametrene kan den såkalte grunnverdi L i langsvilleoverbygningen beregnes:

[math] L = \left( {4 \cdot E \cdot I_{X-X} \over b \cdot C_{RES.}} \right)^{1 \over 4} [/math]

(4.109)

Figur 4.21 Bøyelinje og momentlinje for enkeltlast Q_KV.STAT.

5.9 Beregning av spenning, moment og deformasjon

Nedsenkingen av skinnen i avstand x fra lastens angrepspunkt kan uttrykkes ved følgende ligning:

[math] y(x) = {Q_{KV.STAT.} \over 2 \cdot b \cdot C_{RES.} \cdot L} \cdot \eta [/math]

(4.110)

hvor

[math] \eta = { sin \xi + cos \xi \over e^ \xi} [/math]

(4.111)

Likeledes kan momentet i skinnen i avstand x fra angrepspunktet uttrykkes ved:

[math] M(x) = Q_{KV.STAT.} \cdot {L \over 4} \cdot \mu [/math]

(4.112)

hvor

[math] \mu = {- sin \xi + cos \xi \over e^ \xi} [/math]

(4.113)

I tillegg kan spenningen i u.k. midt på skinnefoten i avstand x beregnes under forutsetning av kjent motstandsmoment for skinnen

[math] \sigma (x)_{U.K.MIDT \ PA \ FOT} = { M(x) \over W_{U.K. FOT}} [/math]

(4.114)

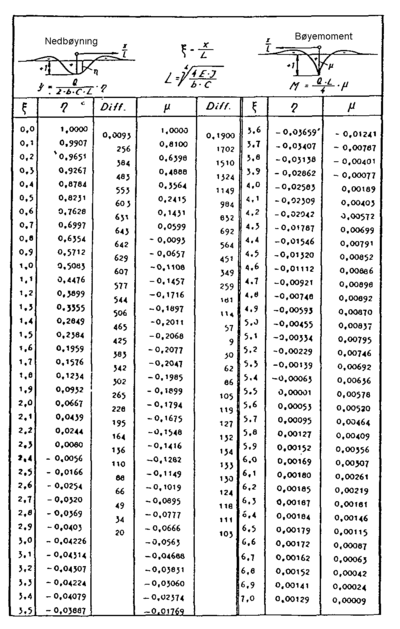
Det kan synes noe komplisert å bruke disse formlene. Det er imidlertid utarbeidet ferdige tabeller for verdiene η og μ som funksjon av ? = x/L. Med hjelp av verdiene for disse faktorene kan bøyelinjen i 4.110 og momentlinjen i 4.112 dermed relativt lett beregnes. Tabellen er vist i avsnitt 5.11.

Støttepunktkraftensom belaster betongsvillen, kan beregnes til :

[math] S(x)=b \cdot sv \cdot p(x) = b \cdot sv \cdot C_{RES.} \cdot y(x) [/math]

(4.115)

Dette under forutsetning av at lasten angriper overbygningen i en avstand x fra svillen.

Direkte under enkeltlast antar hog m verdien 1. Dette gir følgende enkle formler for:

• Nedsenkning av skinnen under enkeltlast :

[math] y_0= {Q_{KV.STAT.} \over 2 \cdot b \cdot C_{RES.} \cdot L} [/math]

(4.116)

• Bøyemoment i skinnen under enkeltlast :

[math] M_0 = Q_{KV.STAT.} \cdot {L \over 4} [/math]

(4.117)

• Spenning i u.k. midt på foten til skinneprofilet under enkellast :

[math] \sigma_{0O.K.MIDTPAFOT} = {M_0 \over W_{U.K.FOT} } [/math]

(4.118)

Endelig kan den såkalte støttepunktkraften S beregnes som er den kraft som forårsaker belastningen på svillene :

[math] S_0 = b \cdot sv \cdot p_0 = b \cdot sv \cdot C_{RES.} \cdot y_0 [/math]

(4.119)

Den beregnede grunnverdi som uttrykkes ved

[math] L= \left( {4 \cdot E \cdot I_{X-X} \over b \cdot C_{RES.}} \right)^{1 \over 4} [/math]

(4.120)

er en funksjon av ballastsifferet C_RES. , treghetsmomentet I _X-X til skinnen, skinnestålets elastisitetsmodul E og bredden b i den tenkte langsvilleoverbygning. E og I _X-X er konstanter for et bestemt skinneprofil. Videre er b en funksjon av den belastede flate til svillen samt svilleavstanden og kan dermed enkelt beregnes. Ballastsifferet beskriver undergrunnens beskaffenhet og hvordan ballastlagetreagerer på undergrunnens egenskaper. Denne faktoren er derfor den eneste parameter som må vurderes visuelt evt. fastsettes ved undersøkelser i undergrunnen. Da ballastsifferet har meget stor innflytelse på resultatet av dimensjoneringen, er det absolutt helt avgjørende at C_RES. (egentlig C _BALLAST) blir vurdert riktig. Dette krever geotekniske kunnskaper om undergrunnen.

Foruten C_RES. utøver også skinnens treghetsmoment I _{X -X} stor innflytelse.

Med hensyn til den beregnede grunnverdi L kan følgende interessante observasjoner gjøres :

• L er identisk med spennvidden for en frittbærende bjelke
• eller 2 x L er identisk med lengden av en stiv bjelke

Figur 4.22 Bildene viser hva grunnverdi L uttrykker.

Parametrene C_RES. og I_X-X påvirker deformasjonen av skinnen på følgende måte :

• Ballastsifferet C_RES.:

Liten verdi av ballastsifferet som indikerer myk undergrunn, betyr lang bøyelinje. Skinnen blir dermed hardt belastet.

Høy verdi av ballastsifferet som indikerer hard undergrunn, betyr kort bøyelinje. Dette medfører at svillen blir utsatt for store påkjenninger.

• Treghetsmomentet I_X-X

om den stive akse til skinneprofilet :

Skinne med stor bærekapasitet forårsaker lengre bøyelinje enn skinne med lavere treghetsmoment .

En kombinasjon av myk undergrunn og skinne med stor bærekapasitet gir en lang bøyelinje. Dette er illustrert i figur 4.23 under. Tilsvarende vil en kombinasjon av hard undergrunn og skinne med liten bærekapasitet bevirke liten bøyelinje. I det første tilfelle blir skinnen hardt belastet og i det andre tilfellet blir svillen utsatt for den største belastningen.

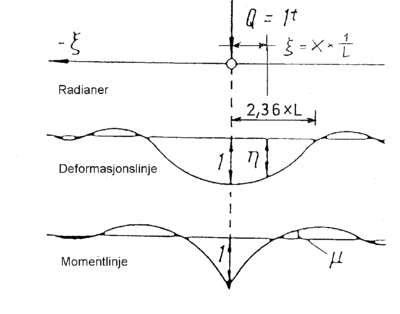
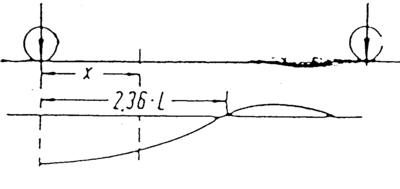
Ved å sette nedbøyningen lik 0 i ligning 4.110 blir ? lik 0. Ved å løse ligning 4.111 med Z= 0 kan det utledes at η antar verdien 2,36. Dette betyr at for η= X/L blir:

• X = 2,36 x L

som er stedet hvor bøyelinjen er lik 0.

Figur 4.23 Illustrasjon av hvordan ballastsifferet og skinneprofilets treghetsmoment influerer på bøyelinjen under belastning. Bøyelinjens nullpunkt er også vist.

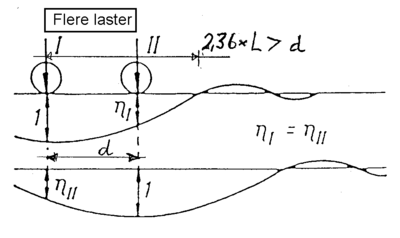
Ved bløt undergrunn og stort skinneprofil kan hjullastf ra nabohjulet bidra til økt belastning og deformasjon for stedet rett under det hjulet som blir betraktet. Dette vil skje når 2,36 x L som er avstanden fra stedet for den betraktede hjullast til nullpunktet for hjullastens bøyelinje, er større enn avstanden til nabohjulet i f.eks. en boggikonstruksjon. De samlede deformasjoner og belastninger ved et slikt lastbilde må beregnes ved superposisjon, dvs. ved addisjon av lasttilfellene. Lastbilde er vist i figur 4.24.

Figur 4.24 Situasjon hvor last 2 innvirker på deformasjonen av skinnen på stedet for last 1. Tilfellet fører til økt belastning på skinnen for dette stedet.

Bøyelinjen eller nedsenkingen av skinnen for 2 laster kan da uttrykkes ved :

[math] y_{(X)KV.STAT.} = {Q_{KV.STAT.1} \over 2 \cdot b \cdot C_{RES.} \cdot L} \cdot \eta_1 + {Q_{KV.STAT.2} \over 2 \cdot b \cdot C_{RES.} \cdot L} \cdot \eta_2 [/math]

(4.121)

Dersom deformasjonen under enkeltlast Q_{KV.STAT. 1} skal beregnes, blir ?₁ lik 1.

Tilsvarende blir momentet eller momentlinjen:

[math] M_{(X)KV.STAT.} = Q_{KV.STAT.1} \cdot L \cdot { \mu_1 \over4} + Q_{KV.STAT.2} \cdot L \cdot {\mu_2 \over4} [/math]

(4.122)

Dersom deformasjonen under enkeltlast Q _{KV.STAT. 1} skal beregnes, blir μ₁ lik 1.

Spenningen i u.k. midt på skinnefoten blir:

[math] \sigma_{(X)} = { M_{(X)KV.STAT.} \over W_{U.K.FOT}} [/math]

(4.123)

Støttepunktkraften S kan beregnes til:

[math] S_{(X)} = b \cdot sv \cdot C_{RES.} \cdot y_{(X)KV.STAT.} [/math]

(4.124)

Det er denne kraften som benyttes til dimensjonering av betongsvillen og som forårsaker bøyemomentene i svillen.

Generelt gjelder for flere laster:

Nedbøyning:

[math] y_{(X)KV.STAT.} = { 1 \over 2 \cdot b \cdot C_{RES.} \cdot L} \cdot \sum_{i=1}^n Q_{KV.STAT.(i)} \cdot \eta_i [/math]

(4.125)

hvor

[math] \eta_i = f( \xi_i ) = f \left( {X_i \over L} \right) [/math]

(4.126)

Momentet:

[math] M_{(X)KV.STAT.} = {L\over 4} \cdot \sum_{i=1}^n Q_{KV.STAT.(i)} \cdot \mu_i [/math]

(4.127)

hvor

[math] \mu_i = f( \xi_i ) = f \left( {X_i \over L} \right) [/math]

(4.128)

Spenningen midt på skinnefot i u.k. :

[math] \sigma_{(X)KV.STAT.} = {M_{(X)KV.STAT.} \over W_{U.K.FOT}} [/math]

(4.129)

Støttepunktkraften blir:

[math] S_{(X)KV.STAT.} = b \cdot sv \cdot C_{RES.} \cdot y_{(X)KV.STAT.} [/math]

(4.130)

Av formlene ovenfor fremgår at faktoren (2 x b x C_RES. x L) kan betraktes som en konstant ved samling av flere krefter over en strekning. Det er i uttrykkene ovenfor også forutsett at den kvasistatiske kraft og dermed også hjullasten varierer. Som regel vil hjullastene i en boggikonstruksjonvære like store og det kan derfor synes unødvendig å innføre Q_KV.STAT. som variabel.

Det er meget sjeldent at det må tas hensyn til flere hjullaster enn 2 i et definert lastbilde for å bestemme de maksimale belastninger. En 3-akslet boggikonstruksjon eksisterer på noen typer av lokomotiv (El14, El15, Di3, Di4) som er i bruk ved NSB i dag. Ved konstruksjon av nye lokomotiv er imidlertid trenden å lage boggikonstruksjoner med 2 aksler.

Videre forekommer det ytterst sjelden at nærmeste aksel fra nabovognen influerer på belastningene i lastbildet til boggikonstruksjonen for den vogn som blir betraktet.

Med den undergrunnen som eksisterer på banenettet til Jernbaneverket og med den avstand som finnes mellom hjulsatsenes senterlinjer i en boggikonstruksjon, vil avstanden fra hjulkraftens angrepspunkt til bøyelinjens nullpunkt (2,36 x L) som regel være mindre enn avstanden mellom hjulsatsenes senterlinjer i en boggikonstruksjon. I de overveiende fleste situasjoner er det altså tilstrekkelig å beregne deformasjoner og spenninger ved å betrakte bare enkeltlasten (ikke ta med nabolaster).

Figur 4.25 Normaltilfelle ved Jernbaneverket hvor det bare er nødvendig å betrakte en last ved deformasjonsberegninger da avstanden mellom hjulsatsene er > 2,36 L.

5.10 Sammendrag og forutsetninger

Ved utvikling av Zimmermanns metode er følgende forutsetninger lagt til grunn:

• Utgangspunktet er den nominelle aksellast P

• Den statiske hjulkraft Q₀ beregnes etter 4.1

• Den kvasistatiske hjulkraft Q_KV.STAT. beregnes etter 4.2

• Dimensjoneringen foregår i kvasistatisk tilstand. Med kvasistatisk tilstand menes at det rullende materieller stillestående, dvs. ikke i bevegelse

• Det er lagt til grunn en ballasttykkelse lik 300 mm mellom u.k. sville og formasjonsplanet

• Det forutsettes ensartet ballastlag

• Det forutsettes at den kvasistatiske hjulkraft Q_{KV. STAT.} angriper sentrisk i skinnehodet

• Det tas ikke hensyn til langsgående krefter

• Det tas ikke hensyn til laterale krefter

• Det forutsettes belastning på svillens underside som for nyjustert spor

Ved dimensjonering betraktes skinnen som en bærebjelke og følgende snittstørrelser beregnes:

• Nedsenking av skinnen

• Momentet i skinnen

• Spenningen i u. k. midt på skinnefoten

• Trykket mot ballasten

• Støttepunktkraftensom er den dimensjonerende kraft for dimensjonering av svillen

5.11 Ballastmatter i ballasten

Ballastmatter i gummi til bruk i overbygningen i den hensikt å dempe strukturstøy fra jernbane er en metode som vinner stadig mer anvendelse. Mattene legges i formasjonsplanet og produseres med forskjellige hardheter.

5.11.1 Grunnleggende prinsipper

Teorien mht. bruk av ballastmatter er meget enkel. Strukturstøy skyldes vibrasjoner som forplanter seg ned gjennom overbygningen og videre ned i undergrunnen ved at det rullende materiell påfører overbygningen dynamiske laster. Disse vibrasjonene må kunne isoleres.

Ved innføring av en tilleggskomponent av elastisk materiale i gummi i formasjonsplanet oppstår det et masse-fjær system som er svingningsdyktig. Gummilaget i formasjonsplanet forårsaker demping av vibrasjonene ved å introdusere bevegelse av selve massen i ballastlaget. Prinsippet er at demping skal kunne skje i et masse – fjær system ved vertikal bevegelse av ballastlaget da dette laget har relativt stor vekt. Det svingningsdyktige masse – fjær systemet tenkes lagt i et betongtrau eller på fjel

Det svingningsdyktige systemet består av vognens boggikonstruksjon (uavfjæret masse), skinner, mellomleggsplater, sviller og ballast av pukk. Det blir antatt at disse komponentene danner et felles svingende system hvor den svingende masse er summen av hjulmasse (uavfjæret masse) og ekvivalent medsvingende spormasse. Denne svingende masse betraktes som et system som blir understøttet av en fjærkraft og en dempekraft som tilsvarer ballastmattens karakteristikker.

Det er påvist at en og samme komponent i sporet blir utsatt for ulik påkjenning fra samme dynamiske kraft mot skinnens kjøreflate. Denne påførte kraften kan beskrives gjennom funksjonen:

[math] F_{PAFORT} = F_0 \cdot sin( \omega t) [/math]

(4.131)

hvor F₀ er amplituden i et kraftforløp. På grunn av bevegelse av det rullende materiell beskrives den påførte kraften som en funksjon av F0uttrykt ved en sinusfunksjon over tid.

Fjærkraften som går gjennom overbygningen og ned til ballastmattene er den kraften som skal isoleres.

Denne kan betegnes ved:

[math] F_T [/math]

(4.132)

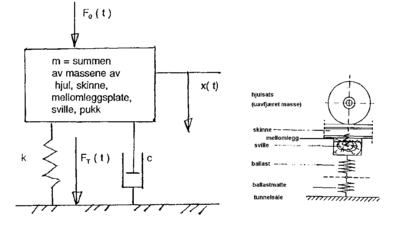
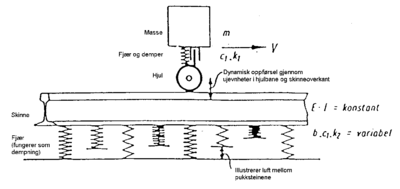
Figur 4.26 viser en modell av overbygningen hvor vognmateriellets hjulsats er inkludert. Modellen beskriver et svingningsdyktig system som består av hjulmasse og ekvivalent spormasse. Systemet betraktes som en enhet hvor alle komponentene er samlet.

Figur 4.26 Svingningsdyktig system som består av hjulsettets uavfjærede masse og ekvivalent spormasse.

Den totale påførte kraft kan beskrives ved:

[math] F_0 = \sqrt {(k - m \cdot \omega^2)^2 + (c \cdot \omega)^2 } \cdot x [/math]

(4.133)

Den overførte kraften settes sammen av fjærkraft og dempekraft:

[math] F_T = \sqrt {k^2 + (c \cdot \omega)^2 } \cdot x [/math]

(4.134)

Her betyr:

• k er ballastmattens fjærstivhet
• m er ekvivalent medsvingende spormasse inkludert uavfjæret masse til boggiens hjulsett
• ? settes lik 2p f
• f er påført frekvens til systemets ekvivalente masse
• c er dempekonstant til ballastmatten
• x er den vertikale bevegelse til det svingningsdyktige systemet

Det blir nå viktig å sammenligne den overførte kraften F_T med den totale påførte kraften F₀:

[math] Q={F_T \over F_0} = {\sqrt {k^2 + (c \cdot \omega)^2} \over \sqrt {(k-m \cdot \omega^2)^2 +(c \cdot \omega)^2 }} [/math]

(4.135)

Det innføres dempingsforholdet D mellom dempingen c i gummimatten og kritisk demping c_KR:

[math] D={c \over (2 \cdot \sqrt{m \cdot k})} [/math]

(4.136)

Videre innføres forholdet ß mellom påført frekvens f i overbygningen ved belastning og overbygningens egenfrekvens f₀:

[math] \beta = {\omega \over \omega_0} ={f \over f_0} [/math]

(4.137)

hvor

[math] \omega = 2 \cdot \pi \cdot f [/math]

(4.138)

og

[math] \omega_0 = 2 \cdot \pi \cdot f_0 [/math]

(4.139)

Med innføring av D og ß kan forholdet mellom den overførte kraften F_T og den påførte kraften F₀ skrives som:

[math] Q={F_T \over F_0} = {\sqrt {1 + (2 \cdot D \cdot \beta)^2} \over \sqrt {(1- \beta^2)^2 +(2 \cdot D \cdot \beta)^2 }} [/math]

(4.140)

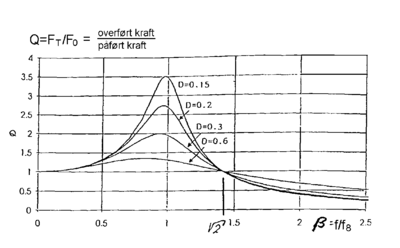
D er som nevnt dempingsforholdet og ß er forholdet mellom påført frekvens og overbygningens egenfrekvens. Dempingsforholdet D representerer forholdet mellom dempingen c i ballastmatten og den kritiske demping. Figur 4.27 viser hvordan Q varierer som funksjon av ß og D.

Figur 4.27 Forholdet mellom den overførte kraft og den totale påførte kraft som funksjon av forholdet mellom påført frekvens og egenfrekvens til overbygningen samt dempingsegenskapene til ballastmatten uttrykt i forhold til kritisk demping.

Figur 4.27 viser at amplitudefunksjonen som er gitt ved forholdet mellom den overførte kraften F_T og den påførte kraften F₀, øker inntil

[math] \sqrt 2 \cdot f_0 [/math]

(4.141)

hvor f₀ er systemets egenfrekvens. Dette betyr at den overførte kraften øker opp til overbygningens egenfrekvens. Den maksimale verdien oppnås ved forholdet ß = f/f₀ = 1. For større verdier enn

[math] \sqrt 2 \cdot f_0 [/math]

(4.142)

blir F_T mindre enn den påførte kraft F₀. Dermed blir det en forbedring mht. strukturstøyen. Derimot ved lave frekvenser blir det en forsterkning av strukturstøyen. Det framgår også at dempingsforholdet D til ballastmattene er av betydning for evnen til å redusere strukturstøyen. En stor verdi av D vil være ønskelig, dvs. en økning av dempeleddet c. Systemets egenfrekvens blir også påvirket av fjærstivheten til mattene og til ballastmassen.

Det er ønskelig å få egenfrekvensen til overbygningen så lav som mulig. Dermed oppnås det en forbedring i strukturstøyen også ved lave frekvenser. Dette gjøres ved å lage ballastmattene så myke som mulig. Av den grunn er en systemfrekvens i området 15 – 20 Hz ønskelig.

For å begrense belastningen på skinnene (spenninger) og for å ivareta tilstrekkelig sikkerhet mht. sporstabilitet bør den totale nedsenkingen i overbygningskonstruksjonen begrenses til 3 – 4 mm i kjøredynamisk tilstand. Det settes derfor krav til ballastmattenes stivhet. Bestemmende parametre er aksellast og hastighet ved framføring av det rullende materiell.

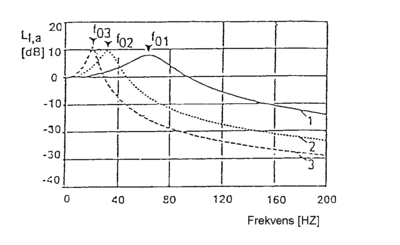
Figur 4.28 viser teoretisk innskuddsdemping for forskjellige konstruksjoner av overbygningen, dvs. støyreduksjoner.

Figur 4.28 Teoretisk innskuddsdemping ved ulike sporkonstruksjoner.

I figur 4.28 viser linjen f₀ 1 at et tradisjonelt spor med tilstrekkelig ballast også har mykhet og dermed gir vibrasjonsisolering, dog ved høye frekvenser.

Linjen f₀₂ viser at et vanlig spor med ballast, men med tillegg av høyelastisk skinnebefestigelse gir en vesentlig bedre innskuddsdemping ved de samme frekvenser.

Linjen f₀₃ viser at konvensjonelt ballastspor med ballastmatte i formasjonsplanetgir vesentlige forbedringer mht. vibrasjonsisolering. Det framgår tydelig at innskuddsdempingen selv ved lave frekvenser er betydelig.

5.11.2 Ballastmattenes innvirkning på ballastsifferet

Ballastmattene legges i overbygningens formasjonsplan på et utjevnende underlag i betong i tunneler. Mattene kan også anvendes på brukonstruksjoner med betongtrau og legges da på et plant underlag av betongdekke. Det forutsettes et ballastlag i pukk mellom mattene og underkant sville på minimum 300 mm.

Ballastmattene har karakteristikker som gjør at overbygningens resulterende ballastsifferendres. Dette har sammenheng med at mattene gjøres så myke som mulig.

Det skal redegjøres for hvordan det resulterende ballastsifferet i overbygningen kan beregnes. Framgangsmåten blir tilsvarende som for beregning av det resulterende ballastsiffer i en overbygning med mellomleggsplate mellom skinne og sville og vanlig ballast i pukklagt direkte på undergrunn. Med innføring av ballastmatten vil det bli et nytt element i overbygningen. Det vises til figur 4.29.

Figur 4.29 Ballastmatte lagt i formasjonsplanet.

Under forutsetning av hard undergrunn dvs. avrettet betonglag på fjelli tunneler eller brukonstruksjon med bærende betongplate, antar overbygnings ballastsiffer en høy verdi:

[math] C_{UNDERGRUNN} \gt 0.40-0.50N/mm^3 [/math]

(4.143)

Ballastmattens statiske siffer må angis:

[math] C_{STAT.MATTE} (N/mm^3) [/math]

(4.144)

Den bestemmes ut fra parametrene aksellast og hastighet til det rullende materiell. For aksellast større enn 160 kN og hastighet større enn 200 km/h settes:

[math] C_{STAT.MATTE} \ge 0.10 N/mm^3 [/math]

(4.145)

Ballasten dvs. pukken lagt på ballastmatten antar også et ballastsiffer:

[math] C_{BALLAST} (N/mm^3) [/math]

(4.146)

Endelig kan mellomleggsplaten angis med et siffer:

[math] C_{MELLOML.} (N/mm^3) [/math]

(4.147)

For å kunne beregne overbygningskonstruksjonens resulterende ballastsiffer er det nødvendig å ha kunnskap om stivhetene til de forskjellige elastiske lagene.

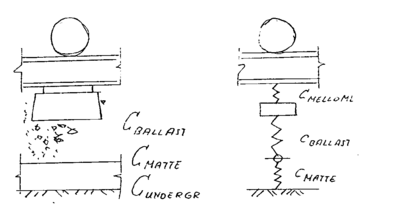
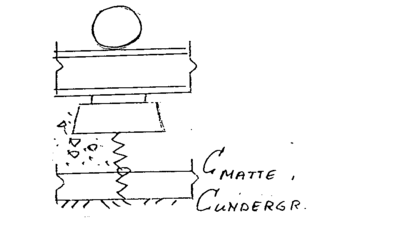
Først betraktes ballastkonstruksjonen, dvs. ballast og ballastmatte lagt på hardt underlag. De 2 lagenes stivheter kan tenkes koblet etter hverandre i en kjede. Det vises til figur 4.30.

Figur 4.30 Seriekobling av stivhetene til ballast og ballastmatte.

Under forutsetning av udempede og frie vibrasjoner angir litteraturen den resulterende stivhet til å være:

[math] {1 \over c_{RES.}} = {1 \over c_{STAT.MATTE}} + {1 \over c_{BALLAST}} [/math]

(4.148)

Nedsenkingen til de enkelte fjærene (ballast og ballastmatte i modellen) påvirkes imidlertid av hardheten til lagene under uttrykt gjennom elastisitetssifferet C. Jo høyere dette sifferet er, jo mindre blir nedsenkingen. Det antas at svillenes belastningsflate er F₁. På grunn av lastfordelingen i ballasten under sville antas ballastmattens belastningsflate å være:

[math] F_2 = 4F_1 [/math]

(4.149)

De enkelte stivheter kan beregnes:

[math] c_{STAT.MATTE} = C_{UNDERG.} \cdot {F_2 \over 2} \ (kN/mm) [/math]

(4.150)

[math] c_{BALLAST} = C_{STAT.MATTE } \cdot {F_1 \over 2} \ (kN/mm) [/math]

(4.151)

Den resulterende fjærstivhet i ballastkonstruksjonen beregnes:

[math] c_{RES.} = { (c_{STAT.MATTE} \cdot c_{BALLAST}) \over (c_{STAT.MATTE} + c_{BALLAST})} \ (kN/mm) [/math]

(4.152)

Dette gir følgende resulterende ballastsiffer i konstruksjonen:

[math] C_{RES.} = {c_{RES.} \over {F_1 \over2}} \ (kN/mm^3) [/math]

(4.153)

Mellomleggsplaten mellom skinne og sville har gitt dynamisk fjærstivhet:

[math] c_{MELLOML. } \ (kN/mm) [/math]

(4.154)

For Pandrol 10 mm gummi mellomlegg i knottet utførelse er denne verdien lik 70 kN/mm.

Dette gir overbygningens totale resulterende stivhet:

[math] {1 \over c_{TOTAL \ STIVHET }} = {1 \over c_{RES.}} + {1 \over c_{MELLOML.}} [/math]

(4.155)

Dette kan omskrives til:

[math] c_{TOTAL \ STIVHET } = { c_{RES.} \cdot c_{MELLOML.} \over c_{RES.} + c_{MELLOML.}} \ (kN/mm) [/math]

(4.156)

Overbygningens resulterende ballastsiffer blir:

[math] C_{TOTAL \ STIVHET } = { c_{TOTAL \ STIVHET } \over {F_1 \over 2}} [/math]

(4.157)

5.11.3 Nødvendige stivheter i ballastmattene

Det stilles krav til den statiske og dynamiske stivhet til ballastmattene. På den ene siden må mattenes statiske stivhet gjøres så lav som mulig da en myk matte demper strukturstøyen effektivt. På den annen side må det settes nedre grenser for den statiske stivhet da en for myk matte fører til større spenninger i skinnene i utmattingstilstanden. Dessuten vil krav til sporstabiliteten og kjøredynamikken kreve en hardere matte. Det er allment akseptert at den samlede nedsenking (summen av statisk og dynamisk nedsenking) fra det rullende materiell ved framføring ikke skal overstige 3 mm.

Det er overbygningens totale ballastsiffer C_{TOTAL STIVHET} som må benyttes for beregning av den opptredende nedsenking. Dette betyr at det er summen av nedsenkingen av hver elastisk komponent (mellomleggsplate, pukk, ballastmatte) i sporet uttrykt ved deres stivheter som blir bestemmende. Aksellasten og hastigheten gir det dimensjonerende grunnlaget for den nødvendige stivhet i overbygningskonstruksjonen. Det er ikke hensiktsmessig å forandre på stivheten til mellomleggsplaten i befestigelsessystemet da denne stivheten må passe inn i befestigelsessystemet. Dette for å unngå bl.a. utmatting av fjærer. Stivheten i ballastlaget kan heller ikke forandres. Dermed må ballastmatten tilpasses den opptredende belastning. Kompromisset består i ikke å gjøre den dynamiske stivhet mykere enn tillatt.

De avgjørende parametre for bestemmelse av den statiske stivhet(det statiske ballastsiffer) er altså aksellasten og hastigheten. Det settes opp følgende tabell :

• Aksellast = 160 kN og hastighet = 120 km/h:

C_STAT.MATTE = 0,02 N/mm³

• Aksellast > 160 kN og hastighet = 120 km/h:

C_STAT.MATTE = 0,03 N/mm³

• Aksellast > 160 kN og 120 < hastighet < 200 km/h:

C_{STAT. MATTE.} = 0,06 N/mm³

• Aksellast > 160 kN og hastighet = 200 km/h:

C_STAT.MATTE = 0,10 N/mm³

Ballastmattene har ved disse egenskaper som ved maksimale belastninger sikrer at summen av nedbøyningen dvs. summen den statiske og dynamiske nedbøyning ikke blir større 3 mm. 3 mm anses å være grenseverdi mht. sikker togfremføring.

Ballastmattene legges på hardt underlag dvs. avrettingslag i betong eller magerbetong i formasjonsplanet . Ballasthøydenfra u.k. sville ned til formasjonsplanet er som normalt 300 mm. Konstruksjonen kan da dimensjoneres etter metoden til Zimmermann med de ballastsiffer som er angitt over.

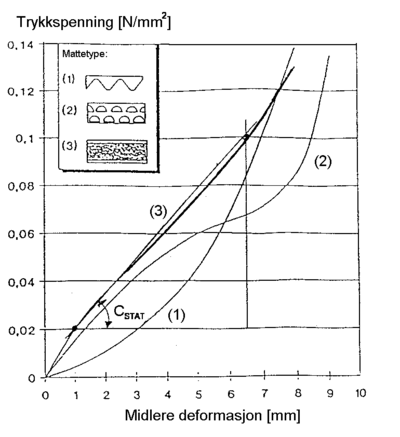
I figur 4.31 er tegnet 3 mulige kurver for den for den karakteristiske fjærlinje.

Figur 4.31 Sammenligning av fjærkarakteristikken for forskjellige typer av ballastmatter. Ballastmatte av type 3 utøver de beste egenskaper.

Kurve 1 fører til progressiv nedsenking for ballastmatte av type 1. Forholdet medfører en massiv sammentrykking. Ballastmatte av type 2 har en s – formet karakteristisk fjærlinje som i vendepunktet for kurven får en økende nedsenking ved konstant trykk. Ut fra kjøredynamisk synspunkt er kurvenes forløp for ballastmattene av type 1 og type 2 meget ugunstige da sporstabiliteten blir forstyrret. Kurve 3 for ballastmatte av type 3 har et homogent deformasjonsforløp og er derfor gunstig for kjøredynamikken til det rullende materiell.

5.11.4 Eksempel på beregning av resulterende ballastsiffer

Det skal vises hvordan det resulterende ballastsiffer for en overbygningskonstruksjon som består av en høyelastisk mellomleggsplate av type Pandrol 10 mm i knottet utførelse og ballast med pukk og tykkelse lik 300mm under u.k. sville samt ballastmatte lagt i formasjonsplanet kan beregnes. Det skal tas utgangspunkt i fjærstivhetene i til de forskjellige elastiske lagene og det forutsettes at fjærene er koblet i serie.

Parametrene er:

• c_MELLOML. = 70 kN/mm

• Aksellast > 160 km/h og hastighet > 200 km/h som medfører at nødvendig stivhet til ballastmatten må være >= 0,10 N/mm³

• Ballastmatten forutsettes lagt på et utjevnende lag av betong på hard undergrunntilsvarende statisk ballastsiffer lik 0,40 N/mm³

• Virksom belastningsflate til betongsville er 570.000 mm²

I figur 4.32 konstruksjonsprinsippet vist.

Figur 4.32 Konstruksjon av overbygningen med ballastmatte.

Den statiske fjærstivhet til ballastmatten:

[math] c_{STAT.MATTE } = C_{UNDERGR. } \cdot { 4F \over 2} \cdot 10^{-3} [/math]

(4.158)

[math] c_{STAT.MATTE } = 0,40 \cdot { 4 \cdot 570000 \over 2} \cdot 10^{-3} = 456 \ kN/mm [/math]

(4.159)

Den statiske fjærstivheten til pukklaget uttrykt som funksjon av stivhetsegenskapene til ballastmatten:

[math] c_{BALLAST } = C_{STAT.MATTE } \cdot { F \over 2} [/math]

(4.160)

[math] c_{BALLAST } = 0,10 \cdot { 570000 \over 2} \cdot 10^{-3} = 28,5 \ kN/mm [/math]

(4.161)

Den resulterende fjærstivhet kan beregnes:

[math] c_{RES.} = { c_{STAT.MATTE} \cdot c_{BALLAST} \over c_{STAT.MATTE} + c_{BALLAST}} \ [/math]

(4.162)

[math] c_{RES.} = { 456 \cdot 28,5 \over 456 +28,5} = 26,8 \ kN/mm [/math]

(4.163)

Dette gir følgende resulterende ballastsiffer i ballastkonstruksjonen:

[math] C_{RES.} = {c_{RES.} \over {F \over 2 } } = { 26,8 \over{570000 \over 2}} \cdot 10^{+3} = 0.094 kN/mm^3 [/math]

(4.164)

Resultatet viser virkningen av ballastmattens innvirkning på ballastsifferet ved bruk av gummimatte. Konstruksjonens totale fjærstivhet blir under forutsetning av seriekobling av fjærene:

[math] c_{TOTAL \ STIVHET } = { c_{RES.} \cdot c_{MELLOML.} \over c_{RES.} + c_{MELLOML.}} \ [/math]

(4.165)

[math] c_{TOTAL \ STIVHET } = { 26,8 \cdot 70 \over 26,8 + 70 } = 19,4 \ kN/mm [/math]

(4.166)

Dermed kan systemets totale ballastsiffer beregnes:

[math] c_{TOTAL \ STIVHET } = { C_{TOTAL \ STIVHET } \over {F \over 2}} [/math]

(4.167)

[math] c_{TOTAL \ STIVHET } = { 19,4 \over {570000 \over 2}} \cdot 10^3 = 0,067 \ N/mm^3 [/math]

(4.168)

Resultatet viser at den totale overbygningskonstruksjonen er blitt meget myk og systemet er vel egnet til å dempe strukturstøy ved lave frekvenser.

5.12 Tabell for η og μ verdier

For å forenkle beregningsmetoden er det utarbeidet tabeller over variablene µ og ? som funksjon av ? . Variabelen µ benyttes i beregningsformelen for bøyemomentet for skinnen og variabelen ? settes inn i formelen for nedsenkingen av skinnen. Variabelen ? er en funksjon av uttrykket x/L, dvs. avstand fra lastens angrepspunkt til det stedet som skal betraktes.

Figur 4.33 Utregnede verdier for variabler i Zimmermanns metode.

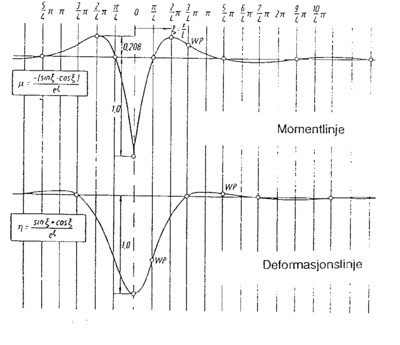
5.13 Eksempel på momentlinje og bøyelinje under enkeltlast

Figur 4.34 viser et eksempel på momentlinje for moment og bøyelinje for deformasjon under enkeltlast. Eksemplet er hentet fra boken "Die Eisenbahnschiene" av Fritz Fastenrath.

Nedsenking:

[math] y={Q \over 2 \cdot b \cdot C \cdot L} \cdot \eta [/math]

(4.169)

Bøyemoment:

[math] M={Q \cdot L \over 4} \cdot \mu [/math]

(4.170)

Grunnverdi:

[math] L= \sqrt[4] {4 \cdot E \cdot I_{X-X} \over b \cdot C} [/math]

(4.171)

[math] \xi={X \over L} [/math]

(4.172)

Figur 4.34 Moment- og deformasjonslinje under enkeltlast.

Figur 4.35 Eksempel på deformasjonslinjen til skinne UIC 60 belastet av en tysk intercity - vogn med aksellast lik 120 kN. Ballastsifferet har verdien C = 0,10 N/mm³.

6 DYNAMISKE LASTER

6.1 Innledning

I de foregående avsnitt er beskrevet hvordan deformasjoner av skinnen samt momenter og spenninger i skinnen kan beregnes med utgangspunkt i den vertikale kvasistatiske hjulkraft Q_KV.STAT. forårsaket av det stillestående materiell i sporet. Det ble forutsatt at kraften angriper sentrisk i skinnehodet.

På grunnlag av omfangsrike målinger i trafikkert spor med pukkballast og drevne aksler er det utviklet en belastnings- og deformasjonsmodell i dynamisk tilstand. Dette betyr at denne modellen tar utgangspunkt i hastigheten til det rullende materiell samt ujevnheter i sporet og på hjulene til det rullende materiell. Modellen bygger på det prinsipp at belastningsverdiene fordeler seg iht. normalfordelingen. Normalfordelingen anvendes som beregningsmodell for å fange opp de maksimale spenninger og deformasjoner som opptrer i kjøredynamisk tilstand. Det forutsettes en statistisk sikkerhet på 99,85 %, dvs. at bare i 0,15 % av lasttilfellene skal beregnede grenseverdier overskrides. Modellen er verifisert ved forsøk i sporet med hastigheter opp til 200 km/h til det rullende materiell.

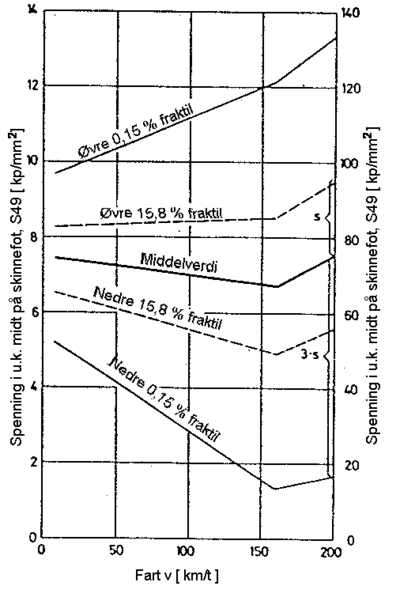
I figur 4.36 er vist resultatet av spenningsmålinger i u.k. midt på skinnefoten ved belastning av 1. aksel til et tysk elektrisk lokomotiv. Det fremgår at det er gjort målinger med hastigheter opp til 200 km/h. Middelverdien samt spredningen av spenningene er beregnet og inntegnet.

Figur 4.36 Resultatet av spenningsmålinger i u.k. midt på skinnefot til skinne S49 under 1. aksel til et elektrisk hurtiglokomotiv til DB AG. Middelverdi til 7 målepunkter samt spredningsområdet er inntegnet. Skinnene er lagt på tresviller.</.

Figur 4.37 Viser normalfordelingen med statistisk sikkerhet P = 68,3 % og P = 99,7 %. Det fremgår av formlene beregningen av middelverdien x og standardavviket s .

Figur 4.38 Viser anvendelse av normalfordelingen for beregning av de største og minste verdier mht. spenninger og deformasjoner som funksjon av hastighet.

Omfangsrike målinger viser at modellen har gyldighet for hastigheter på sporet opp til 200 km/h. Modellen er derfor godt egnet til å dimensjonere overbygningen for norske forhold. Dette gjelder for eksisterende baner og for de nye høyhastighetsbanene (Dobbeltsporet Ski-Moss, Gardermobanen).

Figuren gir følgende opplysninger :

• For hastigheter opp til 200 km/h er middelverdien av spenninger og deformasjoner tilnærmet konstant
• Spredningen av verdiene som uttrykkes ved standardavviket øker med økede hastigheter

Spredningen og dermed størrelsen av de dynamiske krefter skyldes flere forhold:

• Ballastens variable elastisitet på grunn av ulike hulrom under svillen
• Ujevnheter i sporets overflate (bølger, rifler)
• Ujevn overflate i hjulet dvs. ikke helt sirkelformet (hjulslag)
• Ved lasket spor også ujevnheter i laskeskjøten
• De elastiske egenskaper til mellomleggsplaten mellom skinne og sville

6.2 Fremgangsmåte for beregning av de dynamiske krefter

Fremgangsmåten for dimensjonering av de dynamiske krefter blir :

1. Velge dimensjonerende hastighet : V (km/h)

2. Beregne en hastighetsavhengig faktor:

For godstog benyttes formelen:

[math] \nu = 1,0 + {V-60 \over 140} \ge 1,0 [/math]

(4.173)

• for hastigheter i intervallet 60 < V < 200 km/h
• for V ≤ 60 km/h fastsettes L = 1,0

For passasjertog benyttes formelen:

[math] \nu = 1,0 + {V-60 \over 380} \ge 1,0 [/math]

(4.174)

Grunnen til forskjellen i de to formlene er at boggiene i passasjervogner er mye bedre enn i godsvogner.

3. Velge faktor for sporstandard:

k = 0,10 for meget god sporstandard

k = 0,20 for middels god sporstandard

k = 0,30 for dårlig sporstandard

4. Beregne standardavviket:

[math] s= k \cdot \nu [/math]

(4.175)

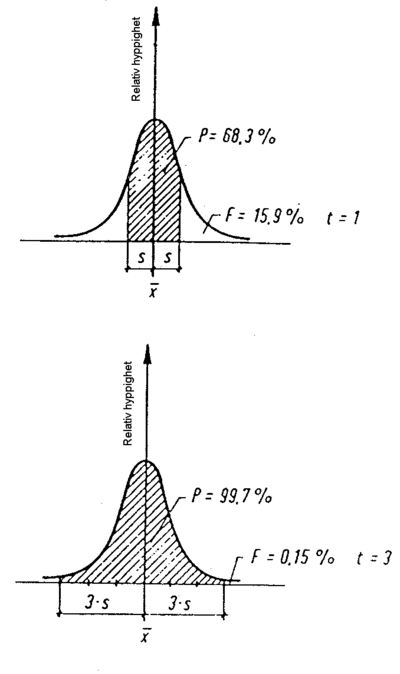
5. Velge statistisk sikkerhet :

t = 3 som betyr en statistisk sikkerhet lik (99,70 + 0,15) % = 99,85 %

t = 2 som betyr en statistisk sikkerhet lik (95,00 + 2,50) % = 97,50 %

t = 1 som betyr en statistisk sikkerhet lik (68,30 + 15,85) % = 84,15 %

6. Beregne ekstremfaktor:

[math] d=(1,0 + t \cdot s) [/math]

(4.176)

Med ekstremfaktor d kan følgende snittstørrelser beregnes i dynamisk tilstand, dvs. summen av kvasistatisk og dynamisk tilstand:

• Den vertikale dynamiske hjulkraft:

[math] Q_{EKSTREM} = Q_{KV.STAT.} \cdot d [/math]

(4.177)

• Moment i skinnen:

[math] M_{EKSTREM} = M_{KV.STAT.} \cdot d [/math]

(4.178)

• Spenning i u.k. midt på skinnefoten:

[math] \sigma_{U.K.MIDTPAFOT,EKSTREMT} = \sigma_{U.K.MIDTPAFOT,KV.STAT.} \cdot d = {M_{EKSTREM} \over W_{U.K.FOT}} [/math]

(4.179)

Evt. kan med kjent motstandsmoment også spenninger på andre steder på skinnetverrsnittet beregnes, f.eks. i o.k. skinnehode.

• Ballasttrykket:

[math] p_{EKSTREM} = p_{KV.STAT.} \cdot d = C_{RES.} \cdot y_{KV.STAT.} \cdot d [/math]

(4.180)

• Støttepunktkraftenfor dimensjonering av svillen:

[math] S_{EKSTREM} = S_{KV.STAT.} \cdot d= b \cdot sv \cdot p_{KV.STAT.}\cdot d = b \cdot sv \cdot C_{RES.} \cdot y_{KV.STAT.} \cdot d [/math]

(4.181)

6.3 Tilleggsspenninger

I tillegg til ovennevnte spenninger grunnet fremføring av det rullende materiell på sporet vil det alltid opptre egenspenninger i skinnetverrsnittet. Disse spenningene fremkommer under produksjonsprosessen av skinnene. I u.k. midt på skinnefoten vil disse egenspenningene være strekkspenninger og de kan fastsettes til:

[math] \sigma_{EGENSPENNING} = 100-200 \ [N/mm^2] [/math]

(4.182)

På grunn av temperaturendringer vil det spesielt i helsveist spor oppstå store spenninger. Disse vil variere alt etter hvor store temperaturendringene er i forhold nøytraltemperaturensom er den temperatur hvor skinnene skal være spenningsfrie. Særlig om vinteren kan strekkspenningene bli til dels meget store ved lave temperaturer med fare for skinnebrudd. Mht. dimensjonering av skinneprofilet kan spenningene beregnes til:

[math] \sigma_{TEMPERATUR} = \alpha_{TH} \cdot \Delta T \cdot E = 1,15 \cdot 10^{-5} \cdot 50 \cdot 2,10 \cdot 10^5 = 120 \ [N/mm^2] [/math]

(4.183)

Det fremgår at det er antatt en maksimal temperaturendring på 50⁰ C ved Jernbaneverket.

6.4 Diskusjon av fremgangsmåten i avsnitt 6.2

Noen av parametrene må bestemmes ved visuell betraktning.

Først må hastigheten bestemmes. Utgangspunktet kan være å velge hastigheten i samsvar med den tillatte hastighet iht. sporgeometrien.

Dimensjoneringen gjennomføres og dersom belastningen ved denne hastigheten blir for stor på grunn av de dynamiske krefter må beregningen gjennomføres en gang til med lavere hastighet. Dimensjoneringen bygger på iterasjonsmetoden. Dette betyr at det er nødvendig å prøve seg frem til resultatene "stemmer".

Dimensjoneringsmetoden forutsetter valg av sporstandarden k. Denne kan som påpekt variere på følgende måte :

• k = 0,1 for meget god overbygningsstandard
• k = 0,2 for middels god overbygningsstandard
• k = 0,3 for dårlig overbygningsstandard

Evt. kan det interpoleres.

For å fastsette riktig k kreves at det gjøres en helhetsvurdering av overbygningen:

• Skinnehodets beskaffenhet (ujevne skjøter samt rifler og bølger på skinneoverflaten)

• Mht. befestigelse er valg av mellomleggsplate avgjørende. F.eks. har Pandrols mellomleggsplate i gummi med knottet utførelse (tykkelse 10 mm) særdeles gode egenskaper mht. å dempe spissbelastningene. Mellomleggsplateav type EVAplast er langt dårligere

• Riktig ballast og ballasttykkelse samt pakningsgrad i sammenheng med type undergrunn for å oppnå en fjærende evne i svillen

Der er viktig å velge den riktige statistiske sikkerhet for den overbygningskomponent som skal dimensjoneres. Følgende regler kan gjøres:

• Mht. til skinner, befestigelse og sviller (betongsviller) må den strengeste statistiske sikkerhet velges. Det er altså nødvendig å sette t = 3, dvs. en statistisk sikkerhet lik 99,85 %. Dette begrunnes med den nære kontakten til det rullende materiell(berøring hjul/skinne). De dynamiske krefter vil derfor gjøre seg gjeldende i særlig stor grad for disse komponentene. Mht. sikkerhet og pålitelighet må det derfor fastsettes de strengeste krav til dimensjonering

• Mht. dimensjonering av ballasten og videre overføring av krefter ned i undergrunnen anbefaler litteraturen at det velges en statistisk sikkerhet lik t = 1, dvs. statistisk sikkerhet = 84,15 %. Dette anses for å være tilstrekkelig da nabosvillene vil sørge for en spredning av den konsentrerte kraften fra hjul/skinne

Det bør bemerkes at dimensjoneringsmetoden ved konstant sporstandard k og konstant statistisk sikkerhet t for en gitt nominell aksellast P gir til resultat at de beregnede momentene i skinnen, spenningene i skinnetverrsnittet samt den samlede nedsenking av skinnen er en funksjon av hastigheten. Dette betyr at modellen ved disse antakelsene forutsetter at det eksisterer en lineær sammenheng mellom belastning/nedsenking og hastighet. Det er høyst usikkert om dette har gyldighet fordi:

• Impulslastene som skyldes skjøter, kan variere

• Vibrasjonslastene som skyldes ujevn skinneoverflate (rifler, bølger), varierer

Men metoden er et meget nyttig verktøy for å kunne beregne de maksimale belastninger i skinnen og nedsenking av skinnen i dynamisk tilstand for hastigheter opp til 200 km/h. Metoden er også verifisert ved omfangsrike målinger i sporet.

7 DIMENSJONERING AV BETONGSVILLEN

7.1 Generelt

Betongsviller stiller strenge krav til ballastens tykkelse og renhet dersom nedknusing av ballasten og svillen skal unngås. Dette gjelder spesielt på hard undergrunn. Nedknusingen skyldes i første rekke betongens manglende elastisitet som medfører høye spenninger i ballasten og i kontaktpunktene mellom hver enkelt stein og svillens underside. Tresviller kan svært ofte være gunstigere enn betongsviller da tresvillene har en viss egen elastisitet. De kan derfor klare seg med f. eks. tynnere ballastlag eller dårligere ballastkvalitet uten at problemer med nedknusing oppstår.

Betongsviller foretrekkes imidlertid på grunn av den store motstandsevnen som disse svillene har mot sideforskyvning. Risikoen for solslyng blir dermed redusert.

7.2 Dimensjoneringsforutsetning

På grunn av betongens manglende elastiske egenskaper og at det opptrer kryp samt svinn i betongen er det meget viktig å dimensjonere betongsvillen for de belastninger som oppstår. Belastningene er den ytre last som skyldes passering av det rullende materiell og indre laster som skyldes at betongen kryper og svinner. Det må også tas hensyn til stålets relaksjon dvs. tap av spennkraft da betongsvillene forspennes. Med forspenning menes at spennkraften opprettholdes ved heft til betongen.

For betongsvillen legges til grunn ved dimensjoneringen et statisk system som er en uendelig stiv bjelke fritt opplagt på 2 støtter. Disse støttene er skinnene. På svillens underside antas ballastspenninger med gitte lastfordelinger.

I avsnitt 6 er redegjort for hvordan støttepunktkraften S_EKSTREM er beregnet. Det er denne kraften som legges til grunn for dimensjonering av betongsvillen. Den virker som opplagerkraft i de 2 støttene dvs. skinnene.

Alt etter undergrunnens beskaffenhet og ballastens tilstand kan fordelingen av ballastspenningene i betongsvillens underside variere mye. For et nyjustert spor vil f. eks. midtpartiet av svillens underside ikke være belastet. Dersom sporet er gammelt dvs. ikke justert på en god stund og sporet i tillegg er blitt utsatt for sterk trafikk vil hele svillens underside bli utsatt for ballastspenninger. Mellom disse ytterpunkter finnes alle tilstander av konsolideringsfaser. Betongsvillene må derfor dimensjoneres for flere opptredende lasttilfeller. Svillene dimensjoneres imidlertid ikke for ballastspenninger som bare opptrer lokalt under svillemidt dvs. at det forutsettes at svillene ikke skal kunne ri under midten. Det er derfor viktig at svillene ikke blir pakket opp under midten. Skulle de få et opplager under midtpartiet er det stor mulighet for at svillene knekker.

7.3 Dimensjonering

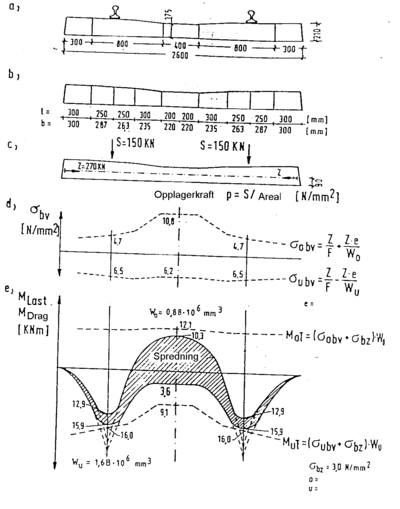
Under er vist dimensjoneringen av den tyske betongsvillen B 70 som benyttes på høyhastighetsbanene til DB AG. I beregningene til DB AG er støttepunktkraften satt til S_EKSTREM = 150 kN. Forspenningskraften er 270 kN. Det er verdt å legge merke til at det forutsettes at betongen kan ta 3 N/mm² strekkspenning. Videre er ved dimensjoneringen de teoretiske støttemomentene over skinnene redusert iht. gitt regelverk.

Figur 4.39 Prinsipp for dimensjonering av betongsville B 70 til DB AG.

Forspenningskraften Z lik 270 kN har 2 oppgaver:

• Den skal hindre riss i den delen av betongtverrsnittet til svillen som blir utsatt for strekkpåkjenninger

• Den skal øke kapasiteten til svillen mht. lastpåkjenninger

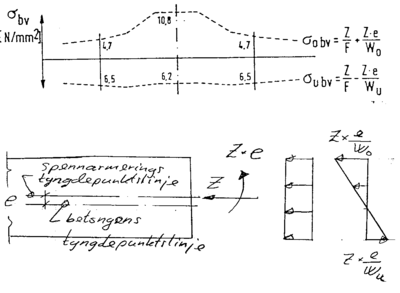
Dette er uttrykt ved spenningene F_BV. Fordi tyngdepunktslinjen til forspenningsarmeringen ikke faller sammen med tyngdepunktslinjen til betongtverrsnittet til svillen, blir kapasitetene over og under tverrsnittets tyngdepunktslinje forskjellig. Dette er vist ved formlene for F_{O BV} og F_{U BV}. Betongtverrsnittets tyngdepunktslinje ligger lavere enn tyngdepunktslinjen til forspenningsarmeringen.

Reduksjonen av de teoretiske støttemomentene over skinnen skyldes at støttepunktkraften har en lastutbredelse lik skinnefotens bredde i o.k. sville. Dessuten forventes en videre lastutbredelse ned gjennom svillen som vist i figur 4.40. Iht. figuren kan støttemomentet reduseres med :

• M = (S/2) x (e/4) = S x e/8

Figur 4.40 Lastutbredelse gjennom svillen.

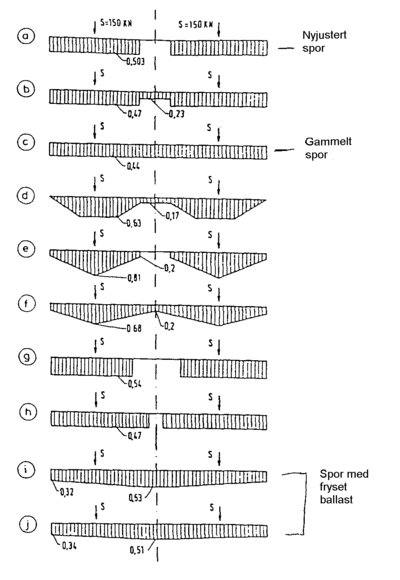
7.4 Mulige ballastspenninger

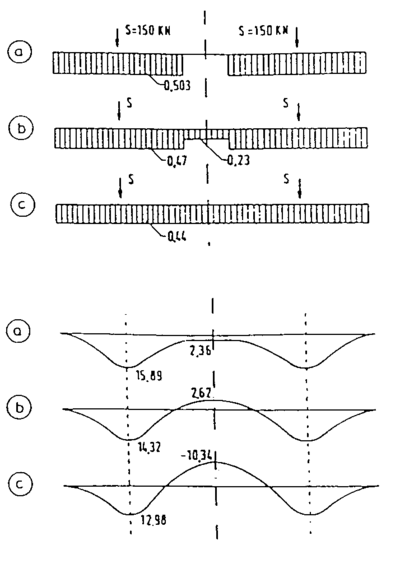
Under er vist mulige fordelinger av ballastspenningene under svillen. Svillene av type B 70 dimensjoneres etter lasttilfellene a, b og c. Lasttilfellene d, e og f dekkes egentlig av de 3 første tilfellene selv om det kan opptre lokale høyere ballastspenninger. Lasttilfelle g er det mulig å unngå ved fornuftig innstilling av pakkaggregatene. Lasttilfelle h er dekket opp av tilfellene a, b og c. Lastbildene i og j må unngås.

Figur 4.41 Mulige lasttilfeller for ballastspenningene under betongsville.

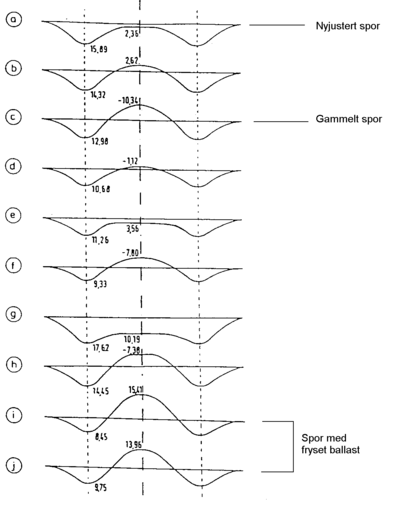
7.5 Tilhørende momentdiagram

Under er vist momentdiagrammer som tilsvarer lasttilfellene i avsnitt 7.4.

Figur 4.42 Tilhørende momentdiagrammer.

7.6 Mulige lastvekslinger ved de forskjellige lasttilfellene

I samsvar med lasttilfellene og tilhørende momentdiagrammerer det foretatt beregninger for antall mulige lastvekslinger på betongsvillene før brudd. Det fremgår med all tydelighet at tilfellene g, i og j absolutt må unngås.

Figur 4.43 Bildet angir antall beregnede lastvekslinger før brudd for betongsville B 70.

7.7 Betongsvillens betydning mht vekten

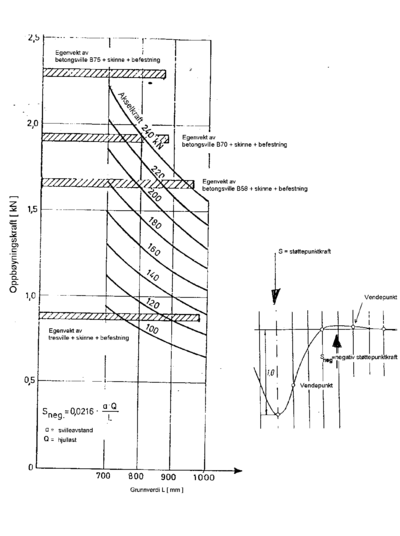
Iht. beregningsmetoden til Zimmermann blir det en heving av sporet foran og bak enkeltaksler og også foran og bak boggier. Dette er påvist både teoretisk og praktisk. Denne oppbøyningen er på ca. 0,10 - 0,30 mm og er nok til at sporet mister sidemotstand. Avgjørende for oppbøyningen av sporet er sporets tyngde. Spesielt er tyngden av betongsvillenen viktig faktor. Figur på neste side illustrerer dette. Figur 4.44 viser hvordan oppbøyningskraften S_NEG. beregnes som funksjon av ballastsifferet C og aksellasten P (angitt med Q på figuren). S_NEG. sammenlignes så med sporets tyngde. Bemerkelsesverdig er det at det er bare betongsville B 75 med lengde 2,80 m som reduserer oppbøyningen ved aksellasterover 200 kN.

Figur 4.44 Sammenligning mellom oppbøyningskraft og sporets vekt.

7.8 NORSKE SVILLER

Ut fra erfaringer og beregninger iht. Zimmermanns modell er det for den nye betongsvillen NSB 93/95 som skal brukes på høyhastighetsbanene, benyttet en støttepunktkraft S_EKSTREM = 150 kN ved dimensjoneringen. Betongsvillen er dimensjonert og forspent for å kunne ta opp ballastspenninger i 3 ulike lastsituasjoner. Disse lasttilfellene samsvarer med lastbildene til den tyske svillen B 70. Oppspenningskraften er 315 kN. Det vises til lasttilfellene med tilhørende momentdiagram under. NSB 95 har en vekt på ca. 270 kg mens B 70 har en vekt på ca. 300 kg. Sville NSB 90 er dimensjonert for S_EKSTREM= 130 kN. Denne svillen har en vekt på ca. 230 kg.

Figur 4.45 Lasttilfeller for ballastspenninger og tilhørende momentdiagram som er benyttet for dimensjonering av den nye betongsvillen.

8 ANSKUELSESBILDE TIL SMITH

8.1 Generelt

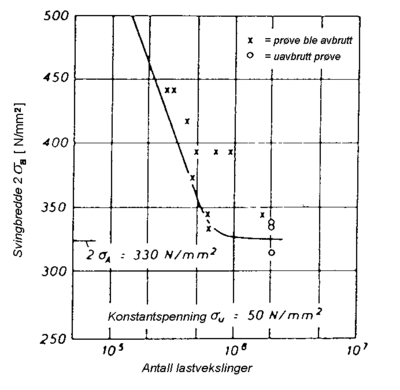
Anskuelsesbilde til Smither et resultat av omfangsrike forsøk som er gjennomført i laboratoriet ved det tekniske universitetet i München, Institut für Eisenbahnwesen. Skinnene er i denne sammenheng blitt utsatt for et stort antall belastninger. Formålet med forsøkene har vært å undersøke de tillatte spenninger på skinnen forårsaket av bøyning ved et stort antall lastvekslinger med varierende belastninger. Med dette som grunnlag er de såkalte Wöhlerkurvene blitt trukket opp for å fastsette utmattingsgrensen for skinner av en bestemt stålkvalitet.

Anskuelsesbilde til Smith har gyldighet for en skinne som blir belastet sentrisk på skinnehodet med en vertikal hjulkraft. Tabellen under viser strekkfasthet, flytegrensen(yield stress) samt tilgjengelige trafikkspenninger(admissible F_d) for skinner med stålkvalitet 700 og 900.

Det er i avsnitt 6.2 påpekt at det eksisterer egenspenninger i skinnen. Egenspenningene fremkommer under produksjonsprosessen og kan settes til 100 N/mm² i u.k. midt på skinnefot.

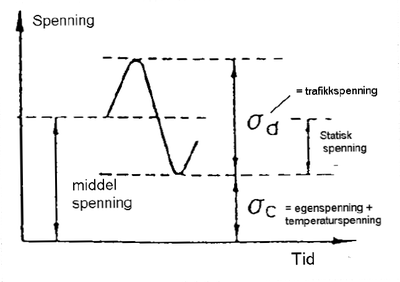
I tillegg opptrer temperaturspenninger som varierer med årstiden og værforhold forøvrig. Spesielt kan strekkspenningene i skinnen ved lave temperaturer om vinteren i helsveiste spor bli til dels meget store. Med økende såkalte konstantspenninger som settes sammen av egenspenningene og temperaturspenningene, avtar den tillatte spenning på grunn av trafikkbelastning. Dette betyr at den såkalte svingbreddefor trafikkbelastningene minker med økende konstantspenninger.

Denne svingbredden for trafikkspenningene sammenlignes så med den beregnede spenning i u.k.midt på skinnefoten F_{U.K. MIDT PC FOT, EKSTREM} i dynamisk tilstand beregnet i avsnitt 6.2. Dersom denne spenningen blir større enn den tillatte svingbredde, må den tillatte hjullastreduseres.

Tabell 4.2 Grenseverdier for forskjellige typer spenninger for skinner av ulik stålkvalitet 700 og 900.

Bruddspenning s U [N/mm2]	Flytespenning s Y [N/mm2]	Tilgjengelige trafikkspenninger
		Lasket spor sC = 80 N/mm2	Helsveist spor sC = 180 N/mm2
700	450	280	230
900	580	320	280

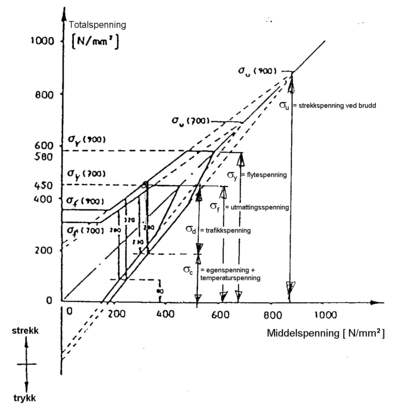
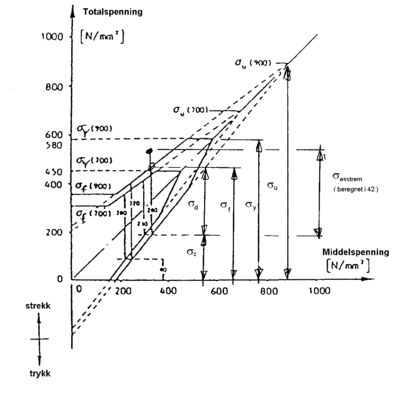
8.2 Anskuelsesbilde til Smith

Figur 4.46 Anskuelsesbilde til Smith.

8.3 Dimensjoneringsprinsipp

I anskuelsesbilde til Smither det en del spenningsbegrep som trenger forklaring:

• F_U er skinnestålets strekkspenning ved brudd (strekkfasthet). Denne spenningen er konstant for en bestemt stålkvalitet

• s_Y er skinnestålets flytegrense. Denne spenningen er også konstant for en bestemt stålkvalitet

• F_EGENSPENNING er skinnestålets egenspenning som oppstår på grunn av produksjonsprosessen. Denne spenningen varierer over tverrsnittet, men kan antas å være 100 N/mm² i u.k. midt på skinnefot

• F_TEMPERATUR er opptredende spenninger i skinnestålet grunnet temperaturendringer

• F_C er konstantspenningen og er summen av egenspenningen og temperaturspenningen, dvs.:

[math] \sigma_{C} = \sigma_{EGENSPENING} + \sigma_{TEMPERATURSPENING} [/math]

(4.184)

• F Der de tillatte dynamiske spenninger på grunn av trafikkbelastning og

tilsvarer svingbredden i Smiths anskuelsesbilde

• F Fer den tillatte utmattingsspenning for en bestemt stålkvalitet:

[math] \sigma_{F} = \sigma_{C} + \sigma_{D} [/math]

(4.185)

Denne spenningen varierer med sammensetningen av F_C og F_D . F.eks. øker F_F med økende konstantspenning og tilsvarende mindre tillatt dynamisk spenning på grunn av trafikkbelastningene. Omvendt vil ved mindre konstantspenninger den tillatte dynamiske spenning kunne økes tilsvarende.

Formel 4.185 kan også skrives:

[math] \sigma_{D} = \sigma_{F} - \sigma_{C} [/math]

(4.186)

Dette betyr at ved gitt konstantspenning F_C kan den tillatte dynamiske trafikkspenning beregnes ved bruk av anskuelsesbilde til Smith.

For den beregnede dynamiske spenning i u.k. midt på skinnefot gjelder :

[math] \sigma_{U.K.MIDTPAFOT,EKSTREM} \le \sigma_{D} [/math]

(4.187)

[math] \sigma_{U.K.MIDTPAFOT,EKSTREM}+\sigma_{C} \le \sigma_{F} [/math]

(4.188)

[math] \sigma_{F} \le \sigma_{Y} [/math]

(4.189)

8.3.1 Tillatt kjøredynamisk spenning

Spenningen σ_{U.K.MIDT PC FOT, EKSTREM} skal diskuteres.

Smiths anskuelsesbilde er utviklet ved omfattende forsøk i laboratoriet under "ideelle" forhold. Dette betyr at innflytelse av værforhold som f.eks. regnvær og fuktighet ikke er tatt inn i utarbeidelsen av bildet. Innflytelsen av egenspenninger i stålet og av temperaturendringer er medtatt gjennom kontantspenningen F_C . Ved å se på spenningen i 4.190 kan det utledes følgende ulikheter dersom utmattingskal unngås under "ideelle" forhold :

[math] \sigma_{U.K.MIDTPAFOT, EKSTREM} \le \sigma_{D} [/math]

(4.190)

[math] \sigma_{U.K.MIDTPAFOT,EKSTREM}+\sigma_{C} \le \sigma_{F} [/math]

(4.191)

[math] \sigma_{F} \le \sigma_{Y} [/math]

(4.192)

Imidlertid må den beregnede kjøredynamiske spenning i 42 reduseres med en faktor for å fange opp innflytelsen av værforhold. Det kan nevnes at DB AG konsekvent for sine Neubaustrecken reduserer de kjøredynamiske spenninger med 50 %. Og det anbefales å benytte samme faktor for alle strekninger til DB AG:

[math] \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot 1,50 \le \sigma_{D} [/math]

(4.193)

[math] \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot 1,50 + \sigma_{C} \le \sigma_{F} [/math]

(4.194)

[math] \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot \nu \le \sigma_{D} [/math]

(4.195)

[math] \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot \nu + \sigma_{C} \le \sigma_{F} [/math]

(4.196)

På grunn av værforholdene i Norge bør også Jernbaneverketbenytte faktor ? = 1,50

I tillegg forlanges en sikkerhetsfaktor. Denne må være høyere jo større hastigheten er. DB AG forlanger for sine Neubaustrecken en sikkerhetsfaktor lik 1,50. For disse strekningene vil da uttrykket bli:

[math] 1,50 \cdot \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot 1,50 \le \sigma_{D} [/math]

(4.197)

[math] 1,50 \cdot \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot 1,50 + \sigma_{C} \le \sigma_{F} [/math]

(4.198)

Generelt kan skrives:

[math] \xi \cdot \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot \nu \le \sigma_{D} [/math]

(4.199)

[math] \xi \cdot \sigma_{U.K.MIDTPAFOT,EKSTREM} \cdot \nu + \sigma_{C} \le \sigma_{F} [/math]

(4.200)

På grunn av lavere hastighet i Norge bør Jernbaneverket benytte faktoren ξ = 1,20.

9 UTMATTING

Det er vel kjent at det kan oppstå utmattingsbrudd i konstruksjoner som blir utsatt for dynamiske påkjenninger. Spenningsamplitudene forårsaket av trafikkbelastningene kan variere mye og bli til dels meget store. Ved overskridelse av skinnestålets utmattingsspenning inntreffer utmatting. Det er da av betydning å kunne beregne skinneprofilets antatte levetid.

9.1 Beskrivelse av N-S kurver

I praksis beskrives utmattingsstyrken for et materiale ved de såkalte Wöhler - kurver eller N - S kurver. Generelt kan dette uttrykkes slik:

[math] N=C \cdot S^{- \beta} , \ \ nar \ \ S \ge S_{UG} [/math]

(4.201)

[math] N= \infty , \ \ nar \ \ S \lt S_{UG} [/math]

(4.202)

Her betyr:

• N = Antall svingninger inntil det oppstår utmattingsbrudd
• S = Spenningsamplituden eller svingbredden i spenningene forårsaket av trafikkbelastningene
• C og $ er materialkonstanter
• S_UG= den såkalte utmattingsgrense eller den tillatte dynamiske spenning på grunn av trafikkbelastningen

Wöhler - kurvene bestemmes eksperimentelt ved anvendelse som regel av sinusbelastninger med konstant amplitude.

En utmattingsskade ΔD_S som induseres av n_S svingninger med konstant amplitude S ≥ S_UG beregnes til:

[math] \Delta D_S = {n_S \over N_S} = {n_s \over C \cdot D^{-S}} = C^{-1} \cdot n_S \cdot S^{-S}, \ \ \ for \ \ n_S \lt N_S [/math]

(4.203)

Her betyr:

• NS= Antall svingninger inntil utmattingsbrudd inntreffer

Det er verdt å legge merke til at utmattingsskaden ΔD_S= 0 dersom S < S_UG .

Den såkalte Palmgren - Minerhypotesensier at utmattingsskader fra svingninger med forskjellige amplitudenivå kan adderes lineært. Den totale utmattingsskade beregnes til:

[math] D= \sum_S \Delta D_S = \sum_S {n_S \over N_S} [/math]

(4.204)

9.2 Utmatting ved bruk av anskuelsesbilde til Smith

Det er allerede nevnt de såkalte Wöhler - kurvene som er et resultat av forsøk med gjentatte lastvekslinger i laboratoriet. I figur under er vist slike forsøk med en UIC 60 skinne av kvalitet 900. Det fremgår at ved få lastvekslinger (10⁵ ) kan spenningsamplitudene dvs. den tillatte svingbredde på grunn av trafikkspenningene være meget store før utmatting inntreffer. Ved stadig lavere verdier for spenningsamplitudene økes antall lastvekslinger før total utmattingsskade inntreffer. For å oppnå lang levetid for en skinne er det derfor nødvendig å holde svingbredden innenfor fastsatte grenseverdier.

Figur 4.47 Bildet viser at ved konstantspenning FC lik 50 N/mm2 kan den tillatte svingbreddeanta meget store verdier ved et begrenset antall lastvekslinger (10⁵ ) før utmattingfinner sted. Ved stadig lavere verdier for den tillatte svingbredde øker antall lastvekslinger før utmatting inntreffer.

Det er interessant å gå tilbake til anskuelsesbilde til Smith. Dersom trafikkspenningene ligger innenfor den tillatte svingbredde F_D ved gitt konstantspenning F_C i anskuelsesbildet betyr dette at utmatting ikke vil skje, dvs. at ΔD_S = 0. Skinnen kan altså bli belastet med et uendelig antall lastvekslinger og skinnen antas å ha svært lang levetid mht. lastvekslinger.

Interessant blir det å undersøke hva som skjer når spenningsamplitudene på grunn av trafikkbelastningene blir større enn den tillatte svingbredde i anskuelsesbilde til Smith ved gitt konstantspenning. Dette kan uttrykkes på følgende måte under hensyntagen til de spenningsbegreper som gjelder i figuren under:

[math] \sigma_{EKSTREM} \gt {\sigma_D \over v \cdot \varsigma } [/math]

(4.205)

[math] \sigma_{EKSTREM} + \sigma_C \gt \sigma_F [/math]

(4.206)

Dessuten bør gjelde:

[math] \sigma_F \le \sigma_ \gamma [/math]

(4.207)

Dette betyr at spenningene under ingen omstendigheter må overskride flytegrensen.

Figur 4.48 Når trafikkspenningene blir større enn σ_D inntreffer utmattingsskader.

9.3 Hypotese til Miner

I hypotesen til Miner arbeides det med begrepene:

• Den tillatte dynamiske spenning i skinnen forårsaket av trafikkbelastningene i en bestemt tidsperiode

• Den tillatte dynamiske spenning i skinnen forårsaket av trafikkbelastningene i en periode av uendelig varighet

Med dette som utgangspunkt kan det beskrives 3 områder mht. levetiden for en skinne. Det tidsbestemte området er nedover bestemt til 10⁵ lastvekslinger. Ved et så lite antall lastvekslinger tas det utgangspunkt i stålets flytegrense for dimensjonering av de tidsbestemte dynamiske spenninger. Disse dynamiske spenningene er mye større enn den tillatte svingbredde i anskuelsesbilde til Smith.

Ved lavere dynamiske spenninger vil levetiden til skinnen øke og det tidsbestemte område vil da bli større.

Dersom lastvekslingene blir større enn 2 x 10⁶ kan det antas en konstant svingbredde i de dynamiske spenningene uten at utmattingsskade inntreffer. Denne svingbredden er den samme som den dynamiske spenningen F_D i anskuelsesbilde til Smith. Det vises til figur 4.49.

Figur 4.49 Diagram som beskriver hypotese til Miner.

Her betyr:

[math] \sigma_D = \sigma_ F - \sigma_ C [/math]

(4.208)

dvs. den tillatte dynamiske spenning i anskuelsesbilde til Smith og

[math] \sigma_T = \sigma_ \gamma - \sigma_ C [/math]

(4.209)

dvs. dynamisk spenning større enn den tillatte spenning i anskuelsesbilde. Diagrammet til Miner viser tydelig at det ut i fra jernbaneteknisk drift er helt nødvendig å tilstrebe at de dynamiske spenninger F_D i skinnen forårsaket av trafikken ikke blir større enn de tillatte spenninger iht. anskuelsesbilde til Smith.

10 SKINNEHODE OG HJULPROFIL

10.1 Generelt

I de foregående avsnitt er skinnen behandlet som bærebjelke for det rullende materiell. Under forutsetning av en vertikal hjulkraft som angriper sentrisk på skinnehode, er opptredende spenninger i u.k. skinne midt på skinnefoten beregnet i kvasistatisk og dynamisk tilstand. Skinnens deformasjon er også blitt betraktet. Videre er utmattingen av skinnene ved dynamisk belasting belyst.

I det etterfølgende skal skinnen betraktes som kjøreveg for det rullende materiell. Ved Jernbaneverket har skinnene en helning med sporplanet på 1:20. Mange land benytter en helning lik 1:40. I berøringspunktet mellom hjul og skinne oppstår det meget store konsentrerte spenninger. Alt etter hvor stor den laterale føringskraft er, betyr denne kraften en økning av spenningene i berøringspunktet mellom hjul og skinne. 3 typer av berøring kan forekomme. Det skilles mellom

• Ettpunktberøring uten anløp.
• Ettpunktberøring med anløp.
• Topunktberøring med anløp.

Figur 4.50 De 3 forskjellige tilfellene ved berøring hjul/skinne.

I trafikkert spor ved høye aksellaster kan det forekomme avskallinger (shelling) på skinnehodet. Dette er sprekker som begynner i en dybde av 5-10 mm under overflaten. Materialet vil etterhvert løsrive seg fra selve skinnehodet. Fenomenet kan tilbakeføres til overskridelse av den varige dynamiske spenningen F_D forårsaket ved trafikkbelastninger i anskuelsesbilde til Smith.

Figur 4.51 Resultat av overskridelse av den varige dynamiske spenningen .

Kjørekantsprekker(head-checks) er en annen type skinnefeil som skyldes høye kontaktspenninger. I motsetning til avskalling initieres sprekkene på overflaten. Kjørekantssprekker kan utvikle seg slik at materialbiter faller av skinnehodet(spalling)

10.2 Belastning av skinnehode

Det er altså nødvendig å undersøke spenningstilstanden i skinnehodet på grunn av hjulbelastningen. Generelt gjelder at ved konstant hjulkraft blir skjærspenningen i skinnehodet større for hjul med mindre radius enn for hjul som har større radier. Ved kombinasjon av små radier og høy hjulbelastning består faren for at skinnematerialet blir overbelastet ved lengre tids bruk. Dette kan føre til kontaktutmattingsskader. Det er gjort omfangsrike forsøk ved universitetet i München som viser spenningstilstanden i det indre av skinnehodet i nærheten av berøringsstedet for hjul og skinne. Ved analyse av resultatene er det tatt utgangspunkt i den såkalte halvromsteori. Denne teorien belyses i figur 4.52:

.

Figur 4.52 Spenningsfordeling i et halvrom langs lastaksen ved sirkelformet berøringsflate og konstant flatespenning for et tverrkontraksjonstall lik 0,30 for stålet.

Figur 4.52 viser at for en sirkelformet belastningsflate med radius a og med konstant trykk p på belastningsflaten utøves det et spenningsforløp i det indre av materialet langs lastaksen som vist. Det forutsettes at stålet har et tverrkontraksjonstall lik 0,3. På figuren er :

• tau = Skjærspenning.
• s_Z = Vertikal trykkspenning.
• s_R = Trykkspenning i radialretningen.

Det kan observeres at den vertikale trykkspenningen s_Z først avtar meget langsomt og deretter hurtigere med økende dybde i materialet. Radialspenningen F_R derimot avtar vesentlig langsommere. Ved hjelp av spenningssirkelen til Mohrkan med utgangspunkt i de 2 hovedspenningene s_Z og s_R den virksomme spenningen under en vinkel på 45⁰ beregnes. Denne resulterende spenningen settes sammen av spenningen i hydrostatisk tilstand og den rene skjærspenningen. Som kjent kjennetegnes den hydrostatiske tilstand av at et legeme blir utsatt for likt trykk på alle sideflater. Det er nok å tenke på et kubisk legeme i en definert høyde under vannets overflate. Dette legeme vil bli utsatt for likt trykk på alle sideflatene. Imidlertid kan for materialet stål den hydrostatiske tilstand neglisjeres når belastningen skal analyseres. Tilbake blir altså den rene skjærbelastning som fører til en vridning. Denne skjærbelastningen må sees i sammenheng med den rene belastning fra selve materialet. Figuren på forrige side viser at hovedskjærspenningen blir 33 % av kontakttrykket p mellom hjul og skinne.

Iht. den anerkjente teori kan hovedskjærspenningene i den videre dimensjoneringen settes til

[math] \tau = 0,30 \cdot p [/math]

(4.210)

Stedet for den maksimale hovedskjærspenning er avhengig av den geometriske formen til berøringsflaten. For et konstant flatetrykk er hovedskjærspenningen lokalisert til en dybde av 0,6 - 1,0 x a. a er radien til den sirkelformede belastningsflate.

Med bakgrunn i ovenstående teori betyr dette for skinneprofilet følgende idet det vises figur 4.53:

Figur 4.53 Antatt belastning av hjul på skinne i berøringspunktet.

Det antas en rektangulær belastningsflate med lengde 2 x a og bredde 2 x b som gir et areal lik 4 x a x b. Det antas videre at

• 2 x b = 12 mm.

Det kan utledes at et jevnt fordelt flatetrykk mellom hjul og skinne kan beskrives ved følgende formel :

[math] \sigma = \sigma_{middel} = 1380 \cdot \left( { Q_{KV.STAT.} \over r} \right)^{1 \over 2} [N/mm^2] [/math]

(4.211)

I ovenstående formler betyr :

• r = Vognens hjulradius i (mm)
• Q_KV.STAT. = Kvasistatisk hjulkraft i (kN) beregnet i (2)

Ovenstående formler gjør det mulig å beregne det jevnt fordelte flatetrykket p mellom hjul og skinne samt hovedskjærspenningen ó_MAX som funksjon av kvasistatisk hjulkraftog hjulradius. Formlene er forenklede i forhold til den strenge teori, men de kan brukes for hjulradier i området 300 < r < 600 mm. Formlene utøver en tilstrekkelig nøyaktighet i dette området.

Imidlertid gir formlene 4.211 og 4.212 ingen informasjon om tillatte grenseverdier. Men med bakgrunn i ovennevnte forhold er det utviklet formler som setter grenseverdier for tillatt hjullast som funksjon av hjulradius. Videre er også den omvendte problemstilling belyst, dvs. at hjulradius kan beregnes som funksjon av hjullast. Skinnestålets strekkfasthet kommer meget sterkt inn i bildet. Skinner med strekkfasthet i brudd lik 880 N/mm² (dvs. skinnekvalitet 900) tåler ved samme hjulradius en langt høyere belastning enn skinner med strekkfasthet i brudd lik 680 N/mm 2 (dvs. skinnekvalitet 700).

10.3 Tillatt aksellast og skjærspenning

Med utgangspunkt i den tillatte skjærspenning kan ved en sammenligning med den opptredende hovedskjærspenning i det indre av skinnehodet(dvs. 5 -10 mm under o.k. av skinnehodet) den tillatte aksellastberegnes. Den nødvendige hjulradius kan også bestemmes.

Det er vanlig å uttrykke den tillatte skjærspenning i forhold til stålets flytegrense. Dette er da også nedfelt i NS 3472 som gir regler for dimensjonering og beregning av stålkonstruksjoner. Dette betyr :

[math] \tau = { f_V \over \sqrt 3} [/math]

(4.213)

Tilsvarende gjelder for skinnestålet :

[math] \tau_{ \ TILLATT} = { \sigma_U \over \sqrt 3} \ [N/mm^2] [/math]

(4.214)

I stedet for stålets flytegrense benyttes skinnens strekkfasthet i brudd. For en skinne med stålkvalitet lik 900 er denne spenningen 880 N/mm² . Da skinnehodetblir utsatt for lastvekslinger, er det nødvendig å fastsette tillatt grenseverdi for skjærspenningen som sikrer lang levetid for skinnen. Omfangsrike forsøk viser at den tillatte spenning i tverretningen i skinnehodet må reduseres med 50 %. Den tillatte skjærspenning kan da beregnes til :

[math] \tau_{ \ TILLATT} = 0,50 \cdot { \sigma_U \over \sqrt 3} \cdot {1 \over \nu} \ [N/mm^2] [/math]

(4.215)

L er en sikkerhetskonstant som skal ta hensyn til spredningen i skinnekvalitet. Denne spredningen er ikke til å unngå ved produksjon av skinner. Det kan nå utledes en formel for den tillatte hjullast som funksjon av hjulradius ved gitt stålkvalitet til skinnen under antagelse av et konstant rektangulært flatetrykk mellom hjul og skinne ved valseberøring. Denne formelen kan skrives som :

[math] Q_{TILLATT,KV.STAT.} = 5,26 \cdot r \cdot \left( { \sigma_U \over \nu} \right)^2 \cdot 10^{-7} \ [kN] [/math]

(4.216)

Tilsvarende gjelder for den minste tillatte hjulradius:

[math] r_{TILLATT} = 1,90 \cdot Q_{KV.STAT.} \cdot \left( { \nu \over \sigma_U} \right)^2 \cdot 10^{6} \ [mm] [/math]

(4.217)

Her betyr :

• s_U = Skinnestålets strekkfasthetved brudd i (N/mm²)
• r = Hjulradius i (mm)
• L = Sikkerhetsfaktor lik 1,10.
• Q_KV.STAT. = Den kvasistatiske hjulkrafti (kN) beregnet i (2).

I formel 4.216 må den beregnede hjullast Q_{TILLATT, KV.STAT.} reduseres med det kvasistatiske tillegget )Q for å beregne hjullasten Q₀. Som det i avsnitt 1 allerede er redegjort for, ligger )Q i området : 0,10 x Q₀ < )Q < 0,30 x Q₀.

Dette betyr at den tillatte hjullast blir :

[math] Q_{0} = Q_{TILLATT,KV.STAT.} - \Delta Q [/math]

(4.218)

Ovenstående formler gjelder for kurver med radius > 500 m. For mindre kurveradier anbefales det å redusere den tillatte hjullasten med 20%. Dette begrunnes med at ved mindre kurveradier og ved bruk av skinnesmøring (for å hindre friksjon mellom hjul og skinner i trangt spor da et slikt spor kan føre til avsporing) vil kontaktfordelingsflaten anta en elliptisk flate. Utgangspunktet for utledningen av formlene var antagelsen om en rektangulær flate.

11 HORISONTALE KREFTER

11.1 Innledning

Den klassiske teori for føring av hjulsatsene beskjeftiger seg med de ideelle krefter uten å ta hensyn til de dynamiske tilleggskrefter som oppstår på grunn av unøyaktigheter i sporet. Tradisjonelt er utgangspunktet for betraktningene for kraftforholdet en boggikonstruksjon som er utformet som en stiv ramme. Hjulsatsene (akslene) er lagret parallelt i denne rammen. Eventuelt gjelder de samme betraktninger for en 2 - akslet vogn. Mellom hjulflens og skinne er det en viss klaring på rett linje. I kurver er klaringen noe større enn forøvrig.

Det er konstruert boggier hvor hjulene er radialinnstilt. Dette gjelder bl.a. for det svenske motorvognsettet X 2000 som er et krengetog. Toget er i regulær trafikk i Sverige. Et sveitsisk lokomotiv LOK 2000 som produseres ved SLM i Winterthur utenfor Zürich, er også satt inn i vanlig kommersiell trafikk. Både X 2000 og LOK 2000 er med stor suksess prøvekjørt på banenettet til Jernbaneverket.

11.2 Bevegelser av vognmateriellet i sporet

Av de kvasistatiske krefterer det spesielt 2 begrep som har interesse. Den ene kraften er den såkalte styringskraften P_A som har betydning for vurdering av slitasjepå skinnehode. Den andre kraften er føringskraften Y_{Fq RING} som har betydning for vurdering av sporets føringsevne samt faren for avsporing. Spesielt føringskraften utledes av friksjonskreftene.

Det skal først kort beskrives hvordan materiellet beveger seg i sporet.

På den rette linje vil hjulkransens konisitetsentrere hjullasten slik at ingen av hjulflensene i alminnelighet berører skinnehodet. Hjulsatsen vil dermed innta en sinusformet bevegelse i horisontalplanet som er ønskelig kjøredynamisk.

I slake kurver gjør omtrent de samme forholdene seg gjeldende. Hjulsatsen sentreres fortsatt ved hjelp av konisiteten til hjulkransen og av overhøyden i kurven. Hjulflensene trer generelt ikke i funksjon og det er bare kontakt mellom hjul og skinne i hjulprofilets indre deler som er hjulkransen og hulkilen. En moderne jernbane med slake kurver trenger teoretisk ingen hjulflenser. Flensene er en sikkerhetsanordning ved feil i sporet.

Under vognens løp i en kurve utøver hjulsatsen en rettlinjet rullebevegelse i vognens lengderetning. Samtidig blir hjulsatsen utsatt for en dreining i horisontalplanet om en pol M som er friksjonsmiddelpunktet. Dette punktet ligger i vognens senterlinje i alminnelighet mellom vognens midtpunkt og bakre aksel. Denne dreiningen forårsaker en glidning som gir friksjonskrefter i anleggspunktene fra hjul mot skinne. Dette er illustrert i figur 4.54. Den horisontale friksjonskraften uttrykkes i forhold til den vertikale hjulkraft Q gjennom friksjonskoeffisienten µ dvs. µ x Q. Friksjonskreftene antas å virke i o.k. av skinnehodet.

Figur 4.54 Horisontale friksjonskrefter i anleggspunktene fra hjul mot skinne ved kjøring i slake kurver.

I de skarpe kurvene ligger hjulflensen eller hulkilen an mot skinnehodet med en horisontalt rettet styringskraft P_A . Samtidig vil vognens dreining fortsatt forårsake en glidning som også i skarpe kurver gir friksjonskrefter, dvs. µ x Q. Disse kreftene virker i o.k. av skinnehodet. Dette er illustrert i figur under. Vinkelen "mellom rulleretningen og tangenten i anløpspunktet kalles anløpsvinkelen.

Figur 4.55 Horisontale friksjonskrefter i anleggspunktene fra hjul mot skinne samt styringskraften ved kjøring i skarpe kurver.

Det er nødvendig å skjelne mellom topunktsberøring og ettpunktsberøring.

Ved topunktsberøring ligger flensen på det ledende hjul an mot skinnehodet i et punkt U som ligger foran og under tangeringspunktet A for rullesirkelen. I berøringspunktet U virker styringskraften P_A . Vertikalkraften Q fordeles egentlig mellom de 2 berøringspunktene, men kan tilnærmet antas å virke i sin helhet i A. Forholdene er skissert i figur . Friksjonskraften µ x Q forutsettes derved å virke horisontalt i o.k. av skinnehodet.

Figur 4.56 Bilde ved topunktsberøring.

Kraftvirkningen i horisontalplanet fra det ledende hjul på skinnehodet settes sammen av styringskraften P_A og friksjonskraften : x Q. For en topunktsberøringgjelder tilnærmet for horisontalkreftene på de enkelte hjul :

Fremre aksel, ytre hjul, dvs. førende hjul :

[math] Y_{FORING} = P_{A} - \mu \cdot Q [/math]

(4.219)

Fremre aksel, indre hjul :

[math] Y_{I} = \mu \cdot Q [/math]

(4.220)

Bakre aksel, ytre hjul :

[math] Y_{A} = Q \cdot cos \phi [/math]

(4.221)

Bakre aksel, indre hjul :

[math] Y_{I} = Q \cdot cos \phi [/math]

(4.221)

Det legges merke til at for fremre aksel er vinkelen n til retningen for friksjonskraften så liten at cosinus-leddet kan sløyfes, dvs. cosφ = 1,00.

Styringskraften P_A bevirker slitasje på skinnehodets vertikale sideflate og på hjulflensen. Den resulterende horisontale føringskraft Y _{Fq RING} mot ytre skinne blir bestemmende for bøyningspåkjenningen i skinnesteget og har betydning for faren for avsporing.

Den samlede horisontalkraft S fra begge skinnehoder ved berøring hjul/skinne overføres til svillene og er bestemmende for sideforskyvning av sporet :

Disse kreftene kan tilnærmet settes til :

Fra fremre aksel :

[math] S_{F} = P_{A} - 2 \cdot Q \cdot cos \phi [/math]

(4.223)

Fra bakre aksel :

[math] S_{B} = 2 \cdot Q \cdot cos \phi [/math]

(4.224)

Friksjonskreftene utgjør en betydelig del av horisontalkreftene.

Ettpunktsberøring oppnås ved å minke anløpsvinkelen "mellom rulleretningen og tangenten i anløpspunktet for berøringen mellom skinne og hjulprofil. Dette oppnås ved slake kurver, elastisk spill i lengderetningen, lenkeaksler og radialinnstilling av hjul. Videre kan friksjonskoeffisienten µ reduseres ved flenssmøring. Styringskraften P_A og vertikalkraften Q angriper i samme punkt. Dette er vist i figur 4.57.

Figur 4.57 Bilde ved ettpunktsberøring.

Ved denne type berøring får det ledende hjul tilnærmet ren rulling. Vertikalkraften Q får en friksjonsvirkning i tangentialplanet T -T, mens horisontalvirkningen av Q blir helt minimal. Horisontalkreftene ved forreste aksel blir tilnærmet :

Fremre aksel, ytre hjul :

[math] Y_{FORING} = P_A [/math]

(4.225)

Fremre aksel, indre hjul .

[math] Y_{I} = - \mu \cdot Q [/math]

(4.226)

Den samlede horisontalkraft beregnes til :

Svillekraft :

[math] S = P_A - \mu \cdot Q [/math]

(4.227)

Det negativet bidraget fra friksjonskreftene reduseres ved ettpunktsberøring. Dette betyr at den samlede horisontale kraft kan bli ganske stor.

11.3 Sentrifugalkraft

Denne kraften opptrer i ytre skinnestreng utover når toget gjennomkjører en kurve med hastighet som er større enn likevektshastigheten. Det vises til figur under.

Figur 4.58 Sentrifugalkraftens betydning.

Sentrifugalkraftener rettet parallelt med horisontalplanet. Men fordi vinkelen " mellom horisontalplanet og sporplanet er meget liten, kan det tilnærmet skrives :

[math] m \cdot cos \alpha \cdot {V^2 \over R} \approx m \cdot {V^2 \over R} [/math]

(4.228)

Ved likevektshastighet i en kurve gjelder :

[math] {V^2 \over R} = m \cdot g \cdot sin \alpha [/math]

(4.229)

hvor uttrykket

[math] m \cdot g \cdot sin \alpha [/math]

(4.230)

er komponenten av vognen parallelt med sporplanet.

Den resulterende horisontalkraft i sporplanet opptrer når :

[math] {V^2 \over R} \gt m \cdot g \cdot sin \alpha [/math]

(4.231)

Dette betyr at den laterale kraft parallelt med sporplanet blir :

[math] Y_{SENT.FUG} = m \cdot \left( {V^2 \over R } - g \cdot { \Delta H \over s} \right) [/math]

(4.232)

Her betyr :

• m = Massen til togmateriellet.
• R = Kurvens radius.

11.4 Vindkraft

Vindkraften settes lik H_W

Figur 4.59 Vindkraft H_W i sporplanet.

11.5 Avsporingsfare

De fleste avsporinger oppstår ved at føringskraften Y_{Fq RING} fra ledende hjul mot ytre skinne i kurve blir for stor i forhold til hjulkraften Q_A. Hjulflensen vil da begynne å klatre opp langs skinnehodet.

Ved avsporinger det alltid snakk om ettpunktsberøring. For å belyse problemet dekomponeres resultanten av de 2 kreftene Q_A og Y_{Fq RING} i en tangentialkraft T langs tangenten mellom hjul og skinne og i en normalkraft N vertikalt på tangenten i berøringspunktet.

Det roterende hjulet kan bare løfte seg dersom hjulflensen finner tilstrekkelig friksjon mot skinnens kjørekant. dvs. når :

[math] \mu \cdot N \ge T [/math]

(4.233)

hvor : er friksjonskoeffisient mellom hjulflens og kjørekant på skinnehodet

Dersom:

[math] \mu \cdot N \lt T [/math]

(4.234)

Den kritiske grenseverdi oppnås ved

[math] \mu \cdot N = T [/math]

(4.235)

eller uttrykt ved friksjonsvinkelen:

[math] \mu = tg \psi = {T \over N} [/math]

(4.236)

Figur 4.60 Avsporingsfare.

Iht. figur 4.60 kan det kritiske forholdet Y_{Fq RING}/Q_A utledes til :

[math] {Y_{FORING} \over Q_A} = tg ( \gamma_A - \rho )= {tg \gamma_A - tg \rho \over 1 + tg \rho \cdot \gamma_A} [/math]

(4.237)

[math] tg ( \gamma_A - \rho )= { tg \gamma_A - \mu \over 1 + \mu \cdot tg \gamma_A} [/math]

(4.238)

hvor µ er hjulets flensvinkel. Denne vinkelen defineres som vinkelen mellom fellestangenten i berøringspunktet og sporplanet. Formelen kalles NADALS formel.

Ovenstående viser at stor friksjon mellom hjul og skinne begunstiger faren for avsporing. Stor friksjon oppstår i trange spor, ved tørre og nye , rustede skinner og ved liten flensvinkel.

Flenssmøring vil motvirke denne situasjonen.

Det fremgår at faren for avsporing oppstår ved et for stort forhold mellom føringskraften Y_{Fq RING} og hjulkraften Q_A. Når dette forholdet overskrider en bestemt verdi, kan hjulflensen klatre opp mot skinnens kjørekant. Det er vognens eller boggiens ledende hjul som kan få denne tendensen. Dette betyr at hjulet i forreste aksel ruller på ytterstrengen i en kurve.

2 situasjoner skal betraktes :

1. Lav hastighet i kurver med konstant overhøyde

Ved lav hastighet i et spor med konstant overhøyde ?H kan hjulkraften Q_A bli meget liten, mens føringskraften Y_A blir relativt stor. Dette fører til at forholdet Y_{Fq RING}/Q_A blir meget stort.

Spesielt kan 2 - akslede godsvogner være utsatt for avsporingsfare ved særlig små hastigheter i skarpe kurver fordi vertikalkraften Q_A på ytre hjul avlastes. Dette har sammenheng med at sentrifugalkraftener mindre enn vognens kraftkomponent parallelt med sporplanet, dvs. at

[math] m \cdot {V^2 \over R} \lt m \cdot g \cdot sin \alpha [/math]

(4.239)

Dessuten vil ugunstig retning på vindkraften forsterke avsporingsfaren.

Figur 4.61 Avsporingsfare i kurve med konstant overhøyde ved framføring av det rullende materiell med lav hastighet.

Faren for avsporinger imidlertid størst i kurver med vindskjevheter fordi avlastningen på førende hjul i ytterstreng her blir ekstra stor :

• Avlastning på grunn av overhøyden ved lav hastighet :

[math] \Delta Q_{(i)} = m \cdot a_Q \cdot {H \over s} [/math]

(4.240)

• Avlastning på grunn av eksentrisk ugunstig plassert godslast

[math] \Delta Q_{(ii)} = G_L \cdot {e_L \over 2s} [/math]

(4.241)

• Avlastning på grunn av sporets vindskjevhet og vognens torsjonsstivhet:

[math] \Delta Q_{(iii)} = stign. \cdot C_{tA} [/math]

(4.242)

• Avlastning på grunn av ugunstig vindretning av vindkraften :

[math] \Delta Q_{(IV)} = H_W \cdot {q \over s} [/math]

(4.243)

Figur 4.62 Avsporingsfare i spor med vindskjevhet ved fremføring av det rullende materiell med lav hastighet.

Den kvasistatiske kraften Q_KV.STAT.,1.1 kan anta svært lave verdier samtidig som de laterale kreftene på grunn av styringskraften P_A kan bli meget store. Dette gjelder spesielt ved lave hastigheter.

11.6 Fare for velting

Ved kjøring i en sirkelkurve i hastigheter større enn likevektshastigheten omlagres hjullastene mellom ytre og indre hjul. For et enkelt, stivt system som vist på figur under skjer velting når den ukompenserte sideakselerasjon

[math] a_Q \ge g \cdot {s \over 2h} [/math]

(4.244)

Det forutsettes at systemet på figuren er stivt. I virkeligheten fjærer vognkassen i forhold til boggirammen. Boggirammen fjærer igjen i forhold til hjulsatsen. Dette betyr at tyngdepunktene for de enkelte legemene forskyver seg og beregningene for veltinger derfor langt mer komplisert enn antydet.

Figur 4.63 Fare for velting i kurve ved for stor hastighet.

Velting kan også inntreffe når det rullende materiell står stille i kurver med for stor overhøyde. Dette har sammenheng med at det opptrer laterale krefter på grunn av tyngdens akselerasjon.

Velting inntreffer når :

[math] \alpha \gt arctan \left( {s \over 2h} \right) [/math]

(4.245)

Figur 4.64 Fare for velting i kurver med for stor overhøyde.

11.7 Kvasistatiske laterale krefter

Summen av de kvasistatiske laterale krefter kan beregnes til :

[math] Y_{KV.STAT.} = Y_{FORING} + Y_ {SENT.FUG} + H_W [/math]

(4.246)

Her betyr :

• Y_{Fq RING} er føringskraften beregnet i 4.219 eller i 4.225.
• Y _SENT.FUG. er sentrifugalkraften beregnet i 4.232.
• H_W er vindkraften.

11.8 Dynamiske laterale krefter

De dynamisk laterale føringskrefteroppstår hovedsaklig på grunn av

• justeringsfeil i sporet
• egengenererte svingninger av det rullende materiell
• ujevn lastfordeling mellom akslene

Det dynamiske tillegget for den kvasistatiske laterale kraft beregnes på samme måte som for det dynamiske tillegget til den kvasistatiske vertikalkraft.

Det tas hensyn til

• statistisk sikkerhet t = 3
• standardavviket s = k x ?

hvor

[math] \nu = 1,0 + { V - 60 \over 180} \ge 1,0 [/math]

(4.247)

for godstog.

For passasjertoggjelder tilsvarende

[math] \nu = 1,0 + { V - 60 \over 380} \ge 1,0 [/math]

(4.248)

Som for de vertikale kreftersettes :

• k = 0,1 for meget god sporstandard
• k = 0,2 for middels god sporstandard
• k = 0,3 for dårlig sporstandard

Den dynamiske føringskraft kan derved uttrykkes ved :

[math] Y_{DYNAMISK} = Y_{KV.STAT.} \cdot (1 + t \cdot s) [/math]

(4.249)

11.9 Beregning av den laterale føringskraft

I praksis er det meget vanskelig å beregne de forskjellige komponentene for den samlede Y - kraft.

Imidlertid er det blitt gjennomført omfangsrike målinger i sporet på Y - kreftene og Q - kreftene ved kjøring av vognmateriell. Med de erfaringer som da er gjort ved disse målingene kan Y - kreftene uttrykkes som funksjon av Q - kreftene. Forholdet mellom de to kreftene beskrives ved et forholdstall k. I figur 4.65 er vist hvordan Y - kraften øker med stadig mindre kurveradier for et tysk lokomotiv samt for godsvogner.

Figur 4.65 Figuren beskriver forløpet av de horisontale krefter som funksjon av kurveradius for lokomotiv og godsvogner.

Målingene viser at k kan variere fra 0,8 til 1,2 ved kjøring i kurver med små radier.

Ved dimensjonering av Y - kreftene er det vanlig å benytte k = 0,6 - 0,8. For kurverike baner med små radier mindre enn 500 m må det brukes en høyere k - faktor enn for øvrige baner.

Med utgangspunkt i det ovenstående kan det skrives generelt :

[math] Y_{KV.SYTAT.} = k \cdot Q_{KV.STAT.} [/math]

(4.250)

[math] Y_{EKSTREMT} = Y_{KV.STAT.} \cdot ( 1 + t \cdot s )= k \cdot Q_{KV.STAT.} \cdot (1 + t \cdot s) [/math]

(4.251)

11.10 Sluttbetraktning

Det er gjort lite for å kvantifisere størrelsen på de forskjellige komponentene for Y - kraften. I stedet er det blitt utført omfangsrike målinger for å få disse kreftene belyst. Det er imidlertid et faktum at laterale justeringsfeilspesielt i kurver har stor innvirkning på både komfort og sporets sidestabilitet. Det samme gjelder de egengenererte svingninger av det rullende materiell på rettlinjet spor.

I " Modern railway track " av Coenraad Esveld beskrives en metode til å beregne Y - kreftene med utgangspunkt i målt geometri. Til slutt følger en oversikt og et sammendrag grafisk for de vertikale og horisontale krefter.

Figur 4.66 Sammendrag av vertikale og laterale krefter.

== BEREGNING AV SKINNESPENNINGER VED SAMVIRKE AV VERTIKALE OG HORISONTALE KREFTER ==

11.11 Innledning

I det foregående er det redegjort for hvordan bøyespenningen i u.k. midt på skinnefoten blir beregnet under forutsetning av en vertikal hjulkraft som angriper sentrisk i skinnehodet. Denne kraften forårsaker bøyning om skinnestålets sterke akse I_{X - X} . Denne lastantagelsen er imidlertid en forenkling av den virkelige situasjonen.

Den vertikale hjulkraftangriper i virkeligheten eksentrisk på skinnehodet og bevirker derved et torsjonsmoment. Samtidig utøves det horisontale føringskrefter som også fører til torsjon. Dessuten bevirker disse kreftene en bøyning om skinnestålets svake akse I_{Y - Y} . For dimensjonering av skinnespenningen i u. k. midt på skinnefoten fører den forenklede lastantagelse om sentrisk vertikal belastning på skinnehode bare til ubetydelige unøyaktigheter. Annerledes blir det når spenningene i u.k. skinnehodet og i u.k. ytterst på skinnefoten skal beregnes. Det vises til figur 4.67.

Figur 4.67 Vertikale og laterale krefter på skinne.

Forsøk i Tyskland har vist at under innflytelse av horisontale føringskrefter i kombinasjon med vertikale hjulkrefter vil det oppstå meget store bøyespenninger på undersiden av skinnehodet og i u.k. ytterst på skinnefoten. Bøyemomentene kan i ugunstigste tilfellet bli opp til 150% større enn de momenter som opptrer i u.k. midt på skinnefoten.

Det er utført studier ( ORE D 71 ( 11 )) som gjør det mulig å beregne materialspenningene på skinnenes sideflate i lengderetningen under belastning av en lateral kraft Y og en eksentrisk vertikal belastning Q.

Denne metoden skal belyses i det etterfølgende.

11.12 Beskrivelse av metoden

Beregningsmetoden for spenningene F_{HODE, U.K.} i undersiden av skinnehodet og F_{FOT, U.K., YTTERST} i undersiden ytterst på skinnefoten er meget bra egnet for vurdering og sammenligning av forskjellige lokomotiv og vognmateriell fordi den laterale føringskraften kommer sterkt inn i bildet.

I figur 4.68 er vist hvordan skinnen blir belastet ved en eksentrisk vertikal hjulkraft og en lateral føringskraft. Videre er vist hvordan kraftbilde deles opp i de enkelte lasttilfeller med tilhørende spenningsbilde i skinneprofilet :

• Lasttilfelle 1 ) Virkning av Q -kraft( Q - kraft sentrisk plassert ).
• Lasttilfelle 2 ) Virkning av torsjonsmomentet på grunn av eksentrisk Q kraft og eksentrisk Y - kraft.
• Lasttilfelle 3 ) Virkning av Y - kraft.

Det fremgår av figuren dreiepunktets beliggenhet.

I tabellen på neste side er vist de forskjellige 8- verdiene for de forskjellige skinneprofilene. 8- verdiene har sammenheng med skinneprofilenes geometri og er utarbeidet for å gjøre det enklere å beregne F_{HODE, U.K.} og F_{FOT, U.K. YTTERST} .

Figur 4.68 Beregning av spenninger i u.k. skinnehode og i u.k. ytterst på skinnefot.

Tabell 4.3 viser λ- verdier for beregning av bøyemomenter i u.k. av skinnehodetog i u.k. ytterst på skinnefot ved eksentrisk belastningmed Q - kraft og Y - kraft.

	Skinneprofil	S49	S54	S64	UIC54	UIC60
	I [cm4]	1819	2073	3252	2346	3055
	Wu[cm3]	248	276	403	313	377
	h’ [cm]	9,9	10,2	12,4	11,9	12,9
Underkant av skinnehode
	?0K	0,0020	0,0017	0,0015	0,0020	0,0018
	? 1K	0,054	0,049	0,048	0,058	0,050
	? 2K	0,016	0,014	0,013	0,019	0,017
	? 3K	0,160	0,140	0,100	0,120	0,110
Underkant av skinnefot
	? 0F	0,0040	0,0036	0,0025	0,0032	0,0027
	? 2F	0,0152	0,0131	0,0095	0,0124	0,0126
	? 3F	0,298	0,261	0,203	0,240	0,229

Av det ovenstående kan formlene utledes til :

u.k. skinnehode:

[math] \sigma_{HODE \ U.K.} = 0,9 \cdot ( \lambda_{1K} \cdot Q \cdot \lambda_{2K} \cdot ( Y \cdot h - Q \cdot e ) + \lambda_{3K} \cdot Y )- \lambda_{0K} \cdot \lambda_M \cdot Q \cdot \left( {El_{XX} \over 64U} \right) ^{1 \over 4} [/math]

(4.252)

u.k. skinnefot ytterst :

[math] \sigma_{FOT \ U.K.YTTERST}= \lambda_{OF} \cdot \lambda_M \cdot Q \cdot \left( {El_{XX} \over 64U} \right) ^{1 \over 4} -0,9 \cdot ( \lambda_{2F} \cdot ( Y \cdot h'-Q \cdot e)-Y \cdot \lambda_{3F}) [/math]

(4.253)

Her betyr :

• 0,9 er en korreksjonskoeffisient for å korrigere forskjellen mellom beregningsmetoden og måleresultatene.
• ó_1K er innflytelsen av spenningsspredningen gjennom skinnehodet.
• ó_2K er innflytelsen av torsjonsmomentet i u.k. skinnehode.
• ó_3K er innflytelsen av horisontal bøyning i u.k. skinnehode.
• ó_OK er innflytelsen av vertikal bøyning i u.k. skinnehode.
• ó_OF er innflytelsen av vertikal bøyning i u.k. ytterst på skinnefot.
• ó_2F er innflytelsen av torsjonsmomentet i u.k. ytterst på skinnefot.
• ó_3F er innflytelsen av horisontal bøyning i u.k. ytterst på skinnefot.
• ó_M er fordelingskoeffisient for akselkreftene beregnet ved hjelp av Zimmermanns innflytelseslinje for momentene i skinnen.
• Elastisitetsmodul for skinnestålet.
• I_{X - X} er skinneprofilets treghetsmoment om den sterke akse
• U er omregnet ballastsiffer for kontinuerlig understøttet bjelke på elastisk underlag i henhold til utgangspunktet for Zimmermanns metode.

· U = k x F/sv hvor

• F = betongsvillens halve bæreflate

sv = svilleavstand

k = ballastkoeffisient i N/mm²

Av formlene fremgår at det er de dynamiske verdier for vertikal hjulkraftog lateral føringskraft som skal benyttes :

• Q = Q_EKSTREM
• Y = Y_EKSTREM

Det er verdt å legge merke til at undergrunnens beskaffenhet og hvordan ballasten gir etter for undergrunnens egenskaper blir tatt hensyn til i de to formlene gjennom det omregnede ballastsifferet U.

Samvirket av Y - og Q - krefter opptrer spesielt i kurver med små radier under 500 meter ved kjøring med tunge lokomotiver samt vogner med tung last.

11.13 Tilleggsspenninger

Det er i formlene 4.252 og 4.253 beskrevet hvordan spenningen i u.k. ytterst på skinnefoten ( F_{FOT, U.K. YTTERST}) og spenningen i u.k. under skinnehodet(F_{HODE, U.K.}) kan beregnes forårsaket av trafikklaster under samvirke av vertikale hjulkrefter og laterale føringskrefter i kjøredynamisk tilstand. I tillegg opptrer også spenninger på grunn av temperaturendringer. Disse spenningene opptrer jevnt fordelt over hele tverrsnittet til skinneprofilet og er enten trykk eller strekkspenninger.

I u.k. ytterst på skinnefoten virker i tillegg aktiverte bøyestrekkspenninger ved kjøring i trange kurver. Disse spenningene skyldes bøyning og beregnes etter følgende formel :

[math] \sigma_{FOT \ U.K.YTTERST}= E \cdot {y \over H} \ \ [N/mm^2] [/math]

(4.254)

Her betyr :

• E = elastisitetsmodulen til skinnestålet [ N/mm²]
• y = halve bredden av skinnefoten [ mm ]
• H = radius i kurven [ mm ]

I likhet med opptredende egenspenninger F E = 100 N/mm² i u.k. midt på skinnefot virker også egenspenninger i u.k. ytterst på skinnefot og i u.k. skinnehode. Forøvrig henvises til figur 4.69 under hvordan egenspenningene opptrer i tverrsnittsprofilet.

Figur 4.69 Egenspenninger i tverrsnittet til skinneprofilet. Dessuten vises også egenspenningeri X - X aksen til skinneprofilet.

11.14 Sammendrag av spenningene

Med hensyn til samvirke av vertikale og laterale krefter i kjøredynamisk tilstand samt egenspenninger og øvrig ytre innflytelse kan spenningene sammenfattes i følgende formler :

Spenning i u.k. på skinnehode :

[math] \sigma_{H} = \sigma_{HODE U.K.} + \sigma_{T} + \sigma_{HODE,E} [/math]

(4.255)

Spenning i u.k. ytterst på skinnefot :

[math] \sigma_{F} = \sigma_{FOTU.K.YTTERST } + \sigma_{T} + \sigma_{HODE,E} + \sigma_{FOTU.K.YTTERST, KURVE } [/math]

(4.256)

Her betyr :

• s_{HODE U.K.} beregnet i 4.252.
• s_{FOT U.K. YTTERST} beregnet i 4.253.
• s_{FOT U.K. YTTERST, KURVE} beregnet i 4.254.
• s_{HODE, E} egenspenning i u.k. skinnehode avleses i figur 4.69 og settes inn i formelen med fortegn.
• s_{FOT, E} egenspenning i u.k. ytterst på skinnefot avleses i figur 4.69 og settes inn i formelen med fortegn.
• s_T= 120 N/mm² spenning som skyldes temperaturendring.

12 BEREGNING AV KREFTER I BEFESTIGELSEN

Befestigelsens oppgave er å hindre skinnene i å velte når det rullende materiell passerer. I tillegg skal den sørge for størst mulig vridningsmotstand mellom skinne og sville. På den måten øker skinnestegets laterale treghetsmoment og med det også sporets sideforskyvningsmotstand i både belastet spor og ubelastet spor.

I figur 58 er vist en forenklet fremstilling over de krefter som virker på skinnen fra en elastisk befestigelse. For de forhold som gjelder i denne figuren kan det vises at befestigelseskraften K₂ er lik :

[math] K_2 = {1 \over b} \cdot \left( Y \cdot h - Q \cdot {b \over 2} \right) -K_0 [/math]

(4.257)

Dette uttrykket oppnås ved å sette summen av alle momentene forårsaket av kreftene lik 0 om punktet B :

3 M = 0 = K₂x b + K₀x b + Q x b/2 - Y x h

Det kan beregnes at utbøyningen i o.k. skinnehode er :

[math] e={h \cdot K_2 \over k \cdot b} [/math]

(4.258)

Her betyr :

• e = horisontal utbøyning i o.k. skinnetopp
• k = skinnebefestigelsens fjærstivhet
• b = skinnefotens bredde
• h = skinnens høyde
• K₀ = forspenningskraft
• Q = Q_EKSTREM i 4.177.
• Y = Y_EKSTREM i 4.251.
• K₂ = befestigelseskraft

Figur 4.70 Krefter som virker på skinnen fra en elastisk befestigelse.

13 TILLATTE SPORKREFTER VED JERNBANEVERKET

Det er utarbeidet en kravspesifikasjon med hensyn til tillatte sporkrefter som utøves av togmateriell i kjøredynamisk tilstand. Det er verdt å legge merke til at grenseverdiene for de dynamiske kreftene er knyttet til sporets tilstand definert ved kvalitetstallet K = 0,60. Ved lavere K - tall må det forventes høyere krefter.

14 BEREGNING AV BJELKE PÅ ELASTISK UNDERLAG

14.1 Bjelke på elastisk underlag

Vi skal her beregne nedbøyning og bøyemoment for bjelken ved hjelp av Winklers hypotese som sier at spenningen er proporsjonal med deformasjonen.

[math] \sigma (x) = C \cdot w(x) [/math]

(4.259)

La oss anta at nedbøyningen kan beskrives av funksjonen w(x).

Vi vet ennå ikke hva slags funksjon w(x) er. Men vi forlanger at w(x) er en symmetrisk funksjon. Skjærkraften i x=0 er 1/2× Q.

Siden spenningen antas proporsjonal med deformasjonen kan vi sette opp følgende likevekt:

[math] {Q \over 2} = \int\limits_{0}^\infty C \cdot w(x) \cdot b \cdot dx [/math]

(4.260)

Her er b bredden av bjelken. Vi kan omskrive 4.260 til:

[math] {Q \over 2} = \int\limits_{0}^x C \cdot w(x) \cdot b \cdot dx + \int\limits_{0}^\infty C \cdot w(x) \cdot b \cdot dx [/math]

(4.261)

Skjærkraften Q(x) er :

[math] Q(x) = \int\limits_{0}^ \infty C \cdot w(x) \cdot b \cdot dx = {Q \over 2} - \int\limits_{0}^x C \cdot w(x) \cdot b \cdot dx [/math]

(4.262)

Partiell derivasjon gir :

[math] {\delta Q \over \delta x} = -C \cdot w(x) \cdot b [/math]

(4.263)

Fra fasthetslære kan man utlede følgende uttrykk for momentet M:

[math] {M \over EI} = { \delta^2 w \over \delta x^2} [/math]

(4.264)

Videre vet vi at skjærkraften fremkommer ved å derivere momentet. Dvs.:

[math] Q= { \delta M \over \delta x} = { \delta^3 w \over \delta x^3} \cdot EI [/math]

(4.265)

Og:

[math] { \delta Q \over \delta x} = { \delta^4 w \over \delta x^4} \cdot EI [/math]

(4.266)

Vi kan nå sette opp følgende likning:

[math] { \delta Q \over \delta x} = -C \cdot w(x) \cdot b = { \delta^4 w \over \delta x^4} \cdot EI [/math]

(4.267)

Vi har dermed fått følgende 4. ordens homogene differensiallikning:

[math] { \delta^4 w \over \delta x^4} + {b \cdot C \over EI} \cdot w = 0 [/math]

(4.268)

Karakteristisk likning:

[math] r^4 + {b \cdot C \over EI} = 0 [/math]

(4.269)

Den karakteristiske likningen har røttene:

[math] r_1 = \sqrt[4] { b \cdot C \over EI} \cdot {1 \over \sqrt 2} \cdot (1+i) = \sqrt[4] {b \cdot C \over 4 \cdot EI} \cdot (1 + i) [/math]

(4.270)

[math] r_2 = \sqrt[4] { b \cdot C \over EI} \cdot {1 \over \sqrt 2} \cdot (-1+i) = \sqrt[4] {b \cdot C \over 4 \cdot EI} \cdot (-1 + i) [/math]

[math] r_3 = \sqrt[4] { b \cdot C \over EI} \cdot {1 \over \sqrt 2} \cdot (-1-i) = \sqrt[4] {b \cdot C \over 4 \cdot EI} \cdot (-1 -i) [/math]

[math] r_4 = \sqrt[4] { b \cdot C \over EI} \cdot {1 \over \sqrt 2} \cdot (1-i) = \sqrt[4] {b \cdot C \over 4 \cdot EI} \cdot (1 - i) [/math]

Dersom den karakteristiske løsningen er på formen:

[math] r = \alpha + i \cdot \beta [/math]

(4.271)

Vet vi at følgende løsning er tilfredsstilt:

[math] w(x) = e^{ - \alpha \cdot x} \cdot ( A \cdot cos( \beta \cdot x) + B \cdot sin( \beta \cdot x)) [/math]

(4.272)

Det er her naturlig å definere den karakteristiske lengden L ved:

[math] L = \sqrt[4] {4 \cdot EI \over b \cdot C} [/math]

(4.273)

Siden vi vet at løsningen er symmetrisk om x=0, kan løsningen nå skrives på formen:

[math] w(x) = e^{ \left\vert x \right\vert \over L} \cdot \left( A \cdot cos \left( { \left\vert x \right\vert \over L} \right)+ B \cdot sin \left( { \left\vert x \right\vert \over L} \right) \right) [/math]

(4.274)

Vi skal nå bestemme konstantene A og B. På grunn av symmetri må vi kreve at:

[math] {\delta w \over \delta x} \Bigg|_{x=0} = 0 [/math]

(4.275)

Som gir at: A = B

Vi kan derfor skrive:

[math] w(x) = A \cdot e^{ - { \left\vert x \right\vert \over L}} \cdot \left( cos \left( { \left\vert x \right\vert \over L} \right)+ sin \left( { \left\vert x \right\vert \over L} \right) \right) [/math]

(4.276)

Konstanten A bestemmer vi nå ved å sette inn forskyvningen w(x) i uttrykket:

[math] {Q \over 2} = \int\limits_{0}^\infty C \cdot w(x) \cdot b \cdot dx [/math]

(4.277)

D.v.s:

[math] {Q \over 2} = C \cdot b \cdot A \cdot \int\limits_{0}^ \infty { cos \left( { \left\vert x \right\vert \over L} \right)+ sin \left( { \left\vert x \right\vert \over L} \right) \over e^ { \left\vert x \right\vert \over L}} dx [/math]

(4.278)

Som vist i bilaget, vet vi at integralet blir lik 1· L. Vises ved å substituere:

[math] u= { x \over L } \Rightarrow dx = L \cdot du [/math]

(4.279)

Med andre ord:

[math] A={Q \over 2 \cdot b \cdot C \cdot L} [/math]

(4.280)

Vi konkluderer dermed at forskyvningen w(x) er gitt ved:

[math] w(x) = {Q \over b \cdot C \cdot L^3} \cdot e^{ { \left\vert x \right\vert \over L}} \cdot \left( cos \left( { \left\vert x \right\vert \over L} \right)+ sin \left( { \left\vert x \right\vert \over L} \right) \right) [/math]

(4.281)

Momentet M(x) er gitt ved:

[math] M(x)= {\delta^2 w \over \delta^2} \cdot EI [/math]

(4.282)

Ved å derivere uttrykket for forskyvningen 2 ganger, kan det vises at:

[math] M(x) = {Q \over b \cdot C \cdot L^3} \cdot e^{ { \left\vert x \right\vert \over L}} \cdot \left( sin \left( { \left\vert x \right\vert \over L} \right)- cos \left( { \left\vert x \right\vert \over L} \right) \right) \cdot EI [/math]

(4.283)

Forenkler vi følgende uttrykk:

[math] {Q \cdot EI \over b \cdot C \cdot L^3} = {Q \cdot L \over 4 } \cdot {4 \cdot EI \over b \cdot C } \cdot {1 \over L^4} = {Q \cdot L \over 4} [/math]

(4.284)

Til slutt konkluderes det med at momentet M(x) er gitt ved:

[math] M(x) = {Q \cdot L \over b \cdot C \cdot L^3} \cdot e^{ { \left\vert x \right\vert \over L}} \cdot \left( sin \left( { \left\vert x \right\vert \over L} \right)- cos \left( { \left\vert x \right\vert \over L} \right) \right) [/math]

(4.285)

14.2 Utledning av ligninger

Utledning av likningen:

[math] {1 \over R} = {M \over EI} [/math]

(4.286)

En bjelke utsettes for ren bøyning. Vi antar at nøytralaksen og arealaksen er sammenfallende. Figur 4.71 nedenfor viser et snitt av bjelken. Den krummer med radius R:

Figur 4.71 Bjelkebøyning.

Bjelken utsettes for et moment M. Momentlikevekt blir:

[math] M= \int\limits_A \sigma \cdot y \cdot dA [/math]

(4.287)

Hooks lov:

[math] \sigma = \epsilon \cdot E [/math]

(4.288)

La oss anta at nøytralaksen har lengden dx. Ut i fra geometrien til figur 4.71 kan vi se at:

[math] {dx \over R} = {(1+ \epsilon) \cdot dx \over R + y} [/math]

(4.289)

Dette gir:

[math] \epsilon = {R +y \over R} -1={y \over R} [/math]

(4.290)

Med andre ord:

[math] \sigma = {E \over R} \cdot y [/math]

(4.291)

Innsatt i vår momentlikevekt:

[math] M= \int\limits_A {E \over R} \cdot y^2 \cdot dA= {E \over R} \cdot I [/math]

(4.292)

Vi kommer dermed fram til det vi skulle utlede :

[math] {1 \over R} = {M \over EI} [/math]

(4.293)

Utledning av likningen:

[math] {M \over EI} = { \delta^2 w \over \delta x^2} [/math]

(4.294)

Figur 4.72 Bjelkeelement.

Et bjelkeelement (del av bjelken) utsettes for et rent bøyemoment. La φ være vinkelen mellom x-aksen og bjelkens nøytralakse.

[math] \phi = { \delta w \over \delta x} [/math]

(4.295)

Geometrisk betraktning gir:

[math] d \phi = { dx \over R} \Rightarrow {1 \over R} = { d \phi \over dx} [/math]

(4.296)

Med andre ord:

[math] {1 \over R } = { \delta \over \delta x} \left( { \delta w \over \delta x} \right) = {M \over EI} [/math]

(4.297)

Løsning av integralet:

[math] \int\limits_0^ \infty {sin(x) + cos(x)\over e^x} dx [/math]

(4.298)

Når det gjelder derivasjon av et produkt har vi at:

[math] (u \cdot v)' = u' \cdot v + u \cdot v' [/math]

(4.299)

Integrerer vi hvert ledd fås:

[math] \int (u \cdot v)' = \int u' \cdot v + \int u \cdot v' [/math]

(4.300)

Regelen for delvis integrasjon blir da:

[math] \int u' \cdot v = u \cdot v - \int u \cdot v' [/math]

(4.301)

Vi ønsker nå å løse integralet:

[math] I= \int\limits_0^\infty e^{-x} \cdot (cos(x) +sin(x)) dx [/math]

(4.302)

[math] I= \left[ -e^{-x} \cdot (cos(x) + sin(x)) \right]_0^\infty - \int\limits_0^\infty -e^{-x} \cdot ( -sin(x) + cos(x))dx [/math]

[math] I= 1+ \int\limits_0^\infty e^{-x} \cdot (cos(x) - sin(x)) = 1+J [/math]

[math] J= \left[ -e^{-x} \cdot (cos(x) - sin(x)) \right]_0^\infty - \int\limits_0^\infty -e^{-x} \cdot ( -sin(x) - cos(x)) [/math]

[math] J= 1-I [/math]

Med andre ord:

[math] I= 1+1-I [/math]

(4.303)

[math] \underline {I= 1} [/math]

---

LITTERATURHENVISNINGER

1. Die Eisenbahnschiene Fritz Fastenrath 1977

2. Modern Railway Track Coenraad Esveld 1989