Sandkasse/Frank/Dimensjonering-AT: Forskjell mellom sideversjoner
(Redigering.) |
(Rettet opp syntaksfeil.) |
||
| (31 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
== Innledning == | == Innledning == | ||
Beregning av strømflyt, termisk belastning og dimensjonering av seriekomponenter i autotransformatorsystem (AT-system) med svært stor belastning kan være utfordrende, fordi strømflyten i lederne ikke er symetrisk. For eksempel vil det på en | Beregning av strømflyt, termisk belastning og dimensjonering av seriekomponenter i autotransformatorsystem (AT-system) med svært stor belastning og kort matestrekning kan være utfordrende, fordi strømflyten i AT-lederne ikke er symetrisk. For eksempel vil det på en jernbanestrekningmed AT-system (elektrisk utforming E) og stor togtrafikk gå mer strøm i positivleder (PL) enn i negativleder (NL). Om en har elektrisk utforming F vil det på samme måte gå mer størm i kontaktledningen (KL). Artikkelen her fokuserer på elektrisk utforming E, samt formler for å finne strømbelastningen i autotransformatorer (AT) og positivleder (PL). | ||
Med stor togtrafikk menes at det på en matestrekning går så mange tog at det for det meste av tiden vil være ett eller flere tog mellom hver | Med stor togtrafikk menes at det på en matestrekning går så mange tog at det for det meste av tiden vil være ett eller flere tog mellom hver AT, eller AT-vindu. Da vil det være mye strøm som overføres enfaset (eller 15 kV-nivå) og mindre tofaset (eller på 30 kV-nivå). Desto større trafikk desto større blir denne tendensen. Motsatt vil større effekt i transitt, altså effekt som overføres fra en matestrekning til en annen eller forbi ett eller flere AT-vinduer, medføre lik strøm i PL og NL. Det vil være det samme som å si at det overføres effekt tofaset. | ||
Det som også kompliserer forholdene er stor effekt i transitt, altså effekt som overføres mellom matestrekninger og forbi koblingshus og matestasjoner. Metoden som det her bygges på forutsetter at det foreligger en trafikksimulering der aktiv og reaktiv effekt, samt spenning, er kjent for innmatepunktene til strekningen som skal analyseres. Disse størrelsen brukes til å finne strømmenes fasevektorer (komplekse størrelser). Det fokuseres dessuten på korte strekninger (kort avstand mellom matestasjoner). Først og fremst vil det være en problmestilling i Oslo-området fordi det her er stor trafikk og bare noen få mil mellom omformerstasjonene. | |||
Første del av artikkelen handler om strømflyten i AT-system med få AT-vinduer. Dette brukes for å finne spesielle korreksjonsfaktorer. Deretter utledes formler for å beregne strømflyt, | Første del av artikkelen handler om strømflyten i AT-system med få AT-vinduer. Dette brukes for å finne spesielle korreksjonsfaktorer. Deretter utledes formler for å beregne strømflyt. Med å kombinere verdier fra simuleringer med formlene som utledes her, kan en fine strøm som funksjon av tid i AT-ledere og AT-er. Ved hjelp av termiske modeller kan en deretter finne temperatur som funksjon av tiden, noe som vil være nyttig ved dimensjonering av autotransformatorer, aluminiumsliner og kraftkabler. | ||
== | == Strømflyt i AT-system på kort matestrekning med tog i alle AT-vinduer == | ||
I appendiks er det vist strømfordeling med last i bare ett AT-vindu for matestrekning med en, to og tre AT-vinduer. Her blir det vist strømfordeling med så stor trafikk at det til enhver tid er tog i alle AT-vinduene. | |||
=== Strømflyt i AT-system med tre AT-vinduer === | === Strømflyt i AT-system med tre AT-vinduer === | ||
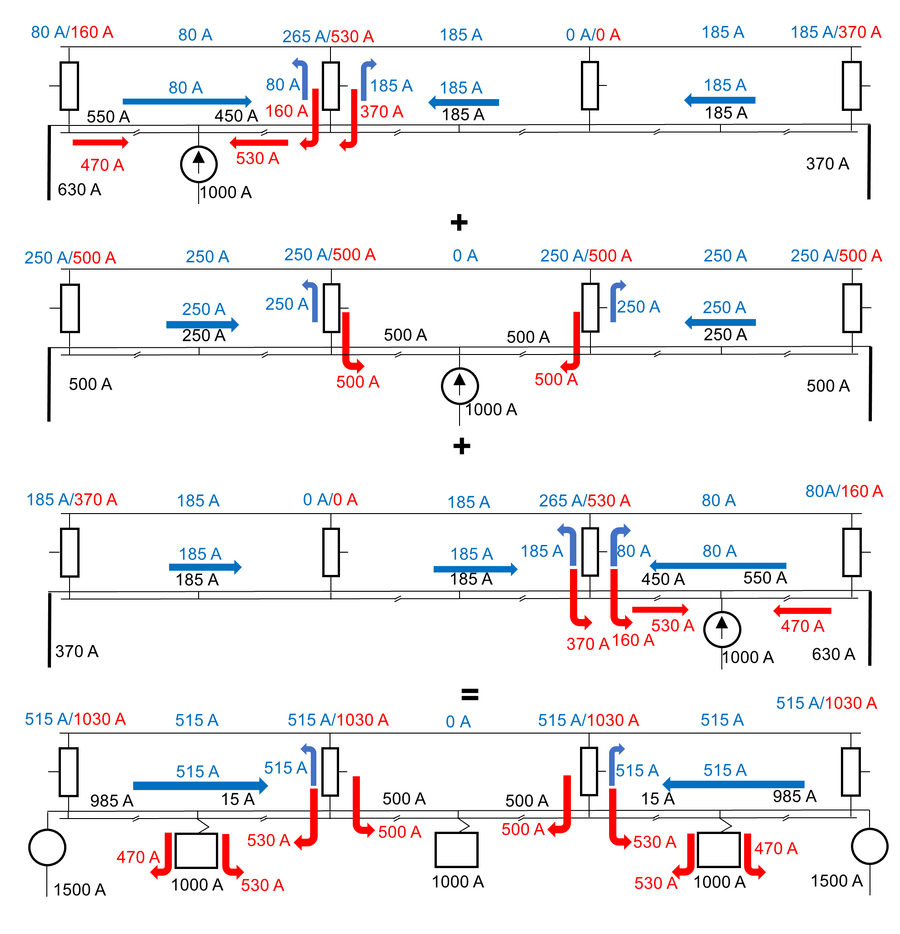
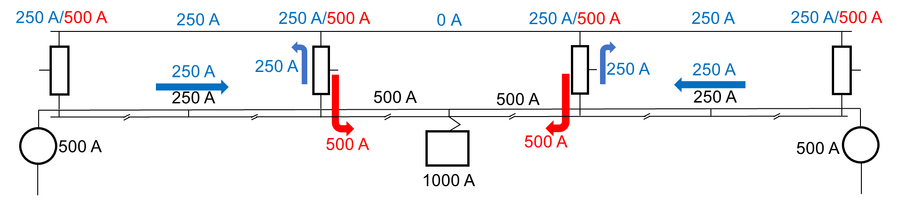
For | For å finne strømmen som flyter i AT-lederne på en matestrekning med tre AT-vinduer undersøkes figuren under og en metodikk basert på superposisjonsteoremet. Først hentes det ut figurer for togplassering og strøm midt i hvert AT-vindu fra appendiks. Togene byttes ut med strømkilder som trekker strøm tilsvarende togene. Summen av strømmene til de tre lastene finnes av superposisjonsteoremet som sier at: ''Den totale strømmen i en hvilken som helst del av en lineær krets tilsvarer den algebraiske summen av strømmer gitt av strømkilde hver for seg. For å bestemme summen av separate strømmer, erstattes alle andre spenningskilder med en kortslutning og alle andre strømkilder med åpne kretser.'' Dermed fås summen som er vist i det nederste linjediagrammet. Som en kan se er strømfordelingen for AT-lederne ved spenningskildene 66 % i PL og 34 % i NL. | ||
[[Fil:Tre tog på strekning med tre AT-vinduer.png|thumb|senter|900px|Strømflyt med tre tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | [[Fil:Tre tog på strekning med tre AT-vinduer.png|thumb|senter|900px|Strømflyt med tre tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | ||
=== Strømflyt i AT-system med to AT-vinduer === | === Strømflyt i AT-system med to AT-vinduer === | ||
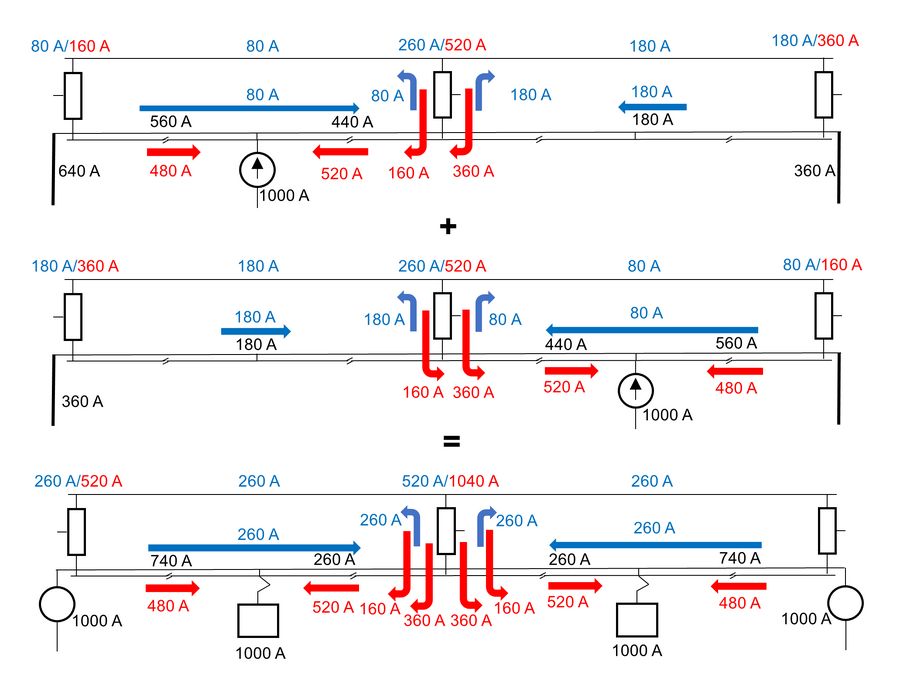
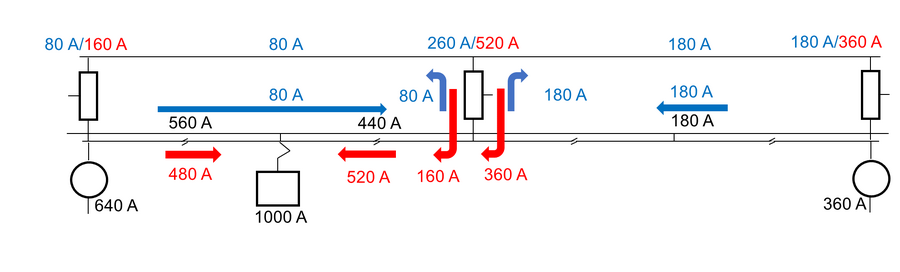
For anslag av strømfordelingen med last midt på hvert av AT-vinduene, tas det utgangspunkt i tilfellet med én last midt på AT- | For anslag av strømfordelingen med last midt på hvert av AT-vinduene, tas det utgangspunkt i tilfellet med én last midt mellom AT-en på en strekning med to AT-vinduer (se appendiks). Det forventes at på en så kort strekning som dette vil begge spenningskildene bidra nokså mye, anslagsvis med fordelingen ⅔ og ⅓ fra spenningskildene henholdsvis til venstre og høyre. I det nederste linjediagrammet er strømmene summert algebraisk. Strømfordelingen for AT-lederne ved spenningskildene er 74 % i PL og 26 % i NL. | ||
[[Fil:To tog på strekning med to AT-vinduer.png|thumb|senter|900px|Strømflyt med to tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | [[Fil:To tog på strekning med to AT-vinduer.png|thumb|senter|900px|Strømflyt med to tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | ||
=== Strømflyt i AT-system med ett AT-vindu === | === Strømflyt i AT-system med ett AT-vindu === | ||
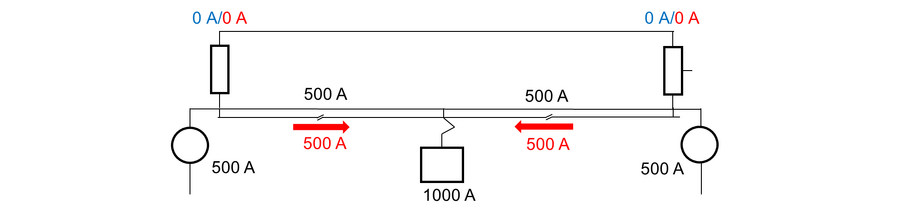
I figuren | I figuren er det vsit strømfordelingen for en matestrekning bestående kun av ett AT-vindu, se appendiks for forklaring. Strømfordelingen for AT-lederne ved spenningskildene er 100 % i PL og 0 % i NL. | ||
[[Fil:Tog midt på strekning med ett AT-vindu.png|thumb|senter|900px|Strømflyt i AT-ledere med en last som trekker 1000 A rett ved autotransformatoren midt på matestrekningen. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå.]] | |||
Tabellen under er en oppsummering av undersøkelsene her og viser usymmetrisk belastning av AT-ledere med en matestrekning bestående av ett, to eller tre AT-vinduer: | |||
{| class="wikitable" style="margin-left:1em; text-align:center" | |||
|+ Strøm i PL og NL nærmest innmatepunktene | |||
! Leder !! Tre AT-vinduer !! To AT-vinduer !! Ett AT-vindu | |||
|- | |||
| Strøm i NL || 515/1500 → 0,34 || 260/1000 → 0,26 || 0/500 →0,0 | |||
|- | |||
| Strøm i PL || 985/1500 → 0,66 || 740/1000 → 0,74 || 500/500 →1,0 | |||
|} | |||
Tabellen viser en interessant tendens, nemmlig at strømmen i NL og PL blir stadige mer jevnt fordelt med økende antall AT-vinduer. Med anslagsvis fem eller flere AT-vinduer ville sannsynligvis strømfordelingen blitt lik mellom de to lederne. | |||
== Beregning av strøm i AT-ledere og autotransformatorer i trafikksimuleringer == | |||
For tog som trekker 1000 A og beveger seg mellom to spenningskilder på en matestrekning med tre, to eller ett AT-vindu, vil strømmen fordele seg nokså ulikt mellom AT-lederne | For tog som trekker 1000 A og beveger seg mellom to spenningskilder på en matestrekning med tre, to eller ett AT-vindu, vil strømmen altså fordele seg nokså ulikt mellom AT-lederne. Dette i motsetning til en matestrekning med mange AT-vinduer der strømmen blir jevn. Tre ting gjør at representasjonen i kapitlet over er en sterk forenkling: | ||
* Spenningskildene er ingen realistisk representasjon av | * Spenningskildene er ingen realistisk representasjon av virkelige omformerstasjoner. I virkeligheten vil blant annet antall omformere i drift, indre impedans og spenningsregulatorer spiller inn. | ||
* Togene trekke stor strøm visse steder (hastighetsøkning), mens de andre steder trekker de moderat (jevn hastighet, liten stigning og rulling) | * Togene trekke stor strøm visse steder (hastighetsøkning), mens de andre steder trekker de moderat (jevn hastighet, liten stigning og rulling), ingen strøm (rulling med liten fall) eller mater inn strøm (regenerativ bremsing i fall). | ||
* Strømfordeling for effekt i transitt er ikke undersøkt, men en del effekt vil overføres på en matestrekning til den neste. Denne effekten fordeler seg likt mellom AT-lederne. | * Strømfordeling for effekt i transitt er ikke undersøkt, men en del effekt vil overføres på en matestrekning til den neste. Denne effekten fordeler seg likt mellom AT-lederne. | ||
For de aktuelle strekningene som en ser på her vil det være stasjoner ved hver av autotransformatorene. Togene kjører ut av stasjonene og akselererer opp i hastighet rett utenfor stasjonene. Det kan derfor godt tenkes stort strømforbruk før togene kommer midt mellom autotransformatorene. Effektfordeling mellom omformerstasjonene som har sammenheng med første kulepunkt blir inkludert i modellene for trafikksimuleringene og vil være gitt i resultatene. | For de aktuelle strekningene som en ser på her vil det være stasjoner ved hver av autotransformatorene. Togene kjører ut av stasjonene og akselererer opp i hastighet rett utenfor stasjonene. Det kan derfor godt tenkes stort strømforbruk før togene kommer midt mellom autotransformatorene. Effektfordeling mellom omformerstasjonene som har sammenheng med første kulepunkt blir inkludert i modellene for trafikksimuleringene og vil være gitt i resultatene. | ||
==== Strøm gjennom | For en sinusformet strøm eller spenning gjelder helt grunnlegende disse funksjonene med hensyn på tiden: | ||
:<math>i(t)=\hat i \cos(\omega t + \theta)</math> | |||
:<math>v(t)=\hat u \cos(\omega t + \theta)</math> | |||
der | |||
:<math>i</math> = momentanverdien av strømmen i tidspunktet t [A] | |||
:<math>u</math> = momentanverdien spenningen i tidspunktet t [V] | |||
:<math>\hat i </math> = maksimumsverdi for strømmen, også kalt amplitude [A] | |||
:<math>\hat v </math> = maksimumsverdi for spenningen, også kalt amplitude [V] | |||
:<math>\omega \, </math> = vinkelfrekvens i radianer [s<sup>-1</sup>] | |||
:<math>t</math> = tiden [s] | |||
:<math>\theta</math> = fasevinkel, faseforskyvning [rad] | |||
Videre i teksten benyttes det viserstørrelser (fasevektor) med uthevede bokstaver, der selve definisjonen er slik: | |||
:<math> \mathfrak{P} (\hat i \cos ( \omega t + \theta)) = \hat i e^{j \theta} = \mathbf{I} </math> | |||
i tillegg til de symbolene som er definert over har en: | |||
:<math> \mathfrak{P}</math> er symbolet for fasevektortransformasjonen | |||
:''e'' = grunntallet for den naturlige logaritmen | |||
:''j'' = den imaginære enheten (<math> \sqrt{-1}</math>) | |||
:'''I''' = strømmen som viserstrørrelse | |||
En sier at fasevektortransformasjonen overfører sinusfunksjonen for strøm eller spenning (til høyre i parantes i formelen over) fra tidsplanet til kompleksplanet. I denne transformasjonen fjernes informasjonen om frekvens og tid. Formen over er på polar form, men kartesisk form er like vanlig, da får uttrykket over denne formen: | |||
:<math> \mathbf{I}= \hat i \cos \theta + j \hat i \sin \theta </math> | |||
I elektroteknikken innføres notasjonen <math>\scriptstyle 1\angle \theta = 1e^{j \theta}</math> som er enklere å skrive når en bruker polar form. | |||
=== Strøm i AT-ledere trafikksimuleringer === | |||
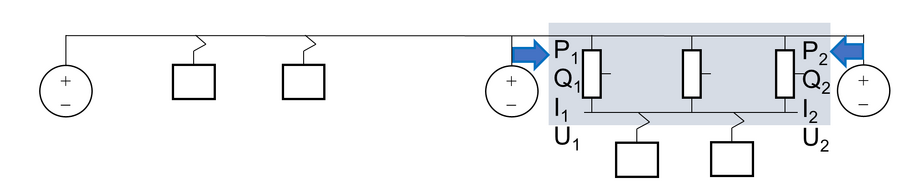
En skal her utlede formler og sette opp en metodikk for belastning av AT-ledere på en strekning vist med en grå boks i hver av illustrasjonene nedenfor. Generelt betraktes en kort matestrekning mellom to omformerstasjoner, som i det øverste bilde nedenfor. Problemstillingen kan også være et strekningsavsnitt med delvis AT-system og BT-system, se det nederste bildet. | |||
[[Fil:Strømmer i et mindre avsnitt med AT-system med to korte matestrekninger.png|thumb|senter|900px|Skisse for problemet med å finne strømmer på en kort matestrekning med AT-system og etterfølgende matestrekning.]] | |||
[[Fil:Strømmer i et mindre avsnitt med AT-system på en lang matestrekning.png|thumb|senter|900px|Skisse for problemet med å finne strømmer på et kort avsnitt med AT-system på en lengre matestrekning.]] | |||
Det vil for hver av disse grå boksene kunne være en strøm- og effektkomponent som går rett gjennom, her kalt ''transittstrøm''. En annen del går inn i boksen og brukes av togene, kalt ''togstrøm''. De blå pilene viser fortegnkonvensjonen som benyttes, slik at strøm og effekt ''inn'' til boksen er togstrøm. | |||
Transittstrømmen som altså går forbi det grå feltet fra venstre mot høyre i figurene er gitt av sammenhengen: | |||
::<math> I_{1-2PLT} = I_{1-2NLT} = \frac {1}{2} \cdot | \mathbf{I_1}- \mathbf{I_2}| </math> | |||
og fra høyre mot venstre i figurene: | |||
::<math> I_{2-1PLT} = I_{2-1NLT} = \frac {1}{2} \cdot | \mathbf{I_2}- \mathbf{I_1}| </math> | |||
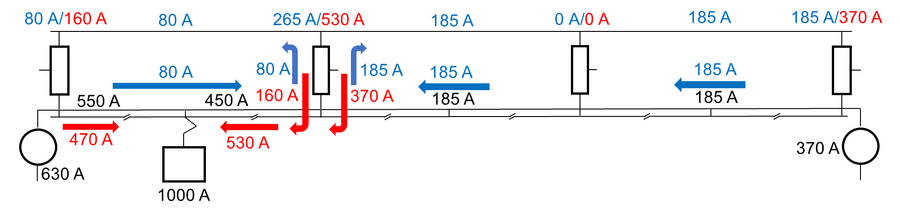
med positive verdier i pilenes retning i figuren og strømmer referert til 15 kV-nivå. En multipliserer med ½ for å ta hensyn til at strømmen ('''''I<sub>1</sub>''''' og '''''I<sub>2</sub>''''') halveres på grunn av doblet spenningsnivå inn i boksene. Grunnen til at en må ta differansen av strømmen '''''I<sub>1</sub>''''' og '''''I<sub>2</sub>''''' når en ønsker å finne '''''I<sub>1-2PLT</sub>''''' og '''''I<sub>1-2NLT</sub>''''' gjennom den grå boksen fra 1 til 2, er at noe av strømmen forbrukes av togene inn i boksen. Det samme gjelder for '''''I<sub>2-1PLT</sub>''''' og '''''I<sub>2-1NLT</sub>'''''. En kan betrakte figuren nedenfor med tre tog for å forsikre seg om at det stemmer. Sammenhengen må gjelde både for en matestrekning, flere AT-vinduer etter hverandre og kun ett AT-vindu. I AT-vinduet til høyre går det inn en strøm på 1500 A fra spenningskilden og ut av AT-vinduet går det en strøm på 500 A (rød pil ved tredje AT), dermed fås 1500–500 = 1000 A, som ved å deles på 2 blir strømmen på 30 kV-nivå (tofaset strøm), altså 500 A. I figuren er det 515 A (blå tall) i NL og PL i det høyre AT-vinduet som overføres på 30 kV-nivå, men noe av denne strømmen blir overført til toget i dette AT-vinduet. Denne delen på 15 A er altså ikke transittstrøm. | |||
Strømmen som tog komsumerer på strekningen innenfor den grå boksen er gitt av: | |||
::<math> I_{tog} = |\mathbf{I_1}+\mathbf{I_2}| </math> | |||
og strømmen i PL som tog komsumerer: | |||
::<math> I_{PLtog} = \frac {1}{2} \cdot k_{PL} \cdot |\mathbf{I_1}+\mathbf{I_2}| </math> | |||
Der en multipliserer med ½ for at summen av strøm inn på AT-vinduet fordeles på lederne fra hver retning frem til toget. I tillegg må korrigeringsfaktoren ''k<sub>PL</sub>'' anvendes for å ta hensyn til asymmetrisk strømfordeling med få AT-vinduer. Her kan en igjen benytte figuren under for å forsikre seg om at formelene stemmer. Summen av strømmene inn til AT-vinduet til høyre er 1500+500 = 2000 A, som ved å deles på 2 blir 1000 A. Altså den strømmen som toget trekker og som går i PL fra hver retning. Strømmen i PL fra høyre er 985 A. Korreksjonsfaktoren k<sub>PL</sub> skal altså benyttes for å justere resultatet for å ta hensyn til ujevn strømfordeling mellom AT-lederne ved få AT-vinduer. | |||
[[Fil:Tog i alle tre AT-vinduer.png|thumb|senter|900px|Strømflyt i AT-ledere med tre tog som trekker 1000 A. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist.]] | |||
Fra simuleringsprogrammene μPAS eller TPSS kan en kun få verdiene for aktiv- og reaktiv effekt i en seriekomponent (med fortegn), samt spenning og strøm. Imidlertid får en ikke strømmene oppgitt som fasevisere. Alle verdiene som fås fra μPAS eller TPSS vil dessuten være referert 15 kV-nivå. For å finne strømmene '''''I<sub>1</sub>''''' og '''''I<sub>2</sub>''''' benyttes sammenhengen: | |||
::<math> \mathbf{I} = \frac {\mathbf{S^*}}{\mathbf{U^*}} = \frac {\mathbf{P}-j\mathbf{Q}}{\mathbf{U}}</math> | |||
Her defineres fasevinkelen til spenningen som referanse og settes til 0°. Det innebærer at fasevinkelforskjellen for spenningen over denne korte strekningen tilnærmes til å være 0°. Videre kan en finne strømmene '''''I<sub>1</sub>''''' og '''''I<sub>2</sub>''''' når effekt og spenning er kjent fra simuleringer: | |||
::<math> \mathbf{I_1} = \frac {\mathbf{P_1}-j\mathbf{Q_1}}{\mathbf{U_1}} \land \mathbf{I_2} = \frac {\mathbf{P_2}-j\mathbf{Q_2}}{\mathbf{U_2}} </math> | |||
Dermed kan en finne strømmen som går i PL ved 1 i de grå boksene i skissene over ved å sette inn for summen av togstrøm ('''''I<sub>PLtog</sub>''''') og transittstrøm ('''''I<sub>PLT</sub>'''''): | |||
::<math> I_{1PL} = \left | \mathbf{I_{1-2PLT}}+\mathbf{I_{PLtog}} \right \vert = \frac{1}{2} \cdot \left | (\mathbf{I_{1}}-\mathbf{I_{2}}) + k_{PL}(\mathbf{I_{1}}+\mathbf{I_{2}}) \right \vert </math> | |||
og ved 2: | |||
::<math> I_{2PL} = \left | \mathbf{I_{2-1PLT}}+\mathbf{I_{PLtog}} \right \vert = \frac{1}{2} \cdot \left | (\mathbf{I_{2}}-\mathbf{I_{1}}) + k_{PL}(\mathbf{I_{1}}+\mathbf{I_{2}}) \right \vert </math> | |||
Her er det første leddet (differansen) strømkomponenten som overføres forbi AT-vinduet(ene), altså transittstrøm, og det andre leddet er strøm som togene på strekningen forbruker, altså togstrøm. | |||
Korreksjonsfaktorene for hver av situasjonene med tre, to og ett AT-vindu finnes ved å settes inn alle størrelsene i uttrykkene over og løse disse ut som ligninger. For situasjonen med tre tog i midten av tre AT-vinduer gir dette: ¼·(1500–1500)+½·''k<sub>PL</sub>''·(1500+1500) = 985, som gir ''k<sub>PL</sub>'' = 0,66. For tilfellet med to tog og to AT-vinduer fås ''k<sub>PL</sub>'' = 0,74 og for ett tog og AT-vindu ''k<sub>PL</sub>'' = 1,0. Dette er de samme tallene som en satte opp i tabellen over som viste usymetrisk belastning mellom NL og PL. Tabellen gjentas her: | |||
{| class="wikitable" style="margin-left:1em; text-align:center" | |||
|+ Korreksjonsfaktorer for strøm i PL ved innmating | |||
! !! Tre AT-vinduer !! To AT-vinduer !! Ett AT-vindu | |||
|- | |||
| ''k<sub>PL</sub>'' || 0,66 || 0,74 || 1,0 | |||
|} | |||
Korreksjonsfaktoren vil som tidligere nevnt gå mot 0,5 om det er anslagsvis fem AT-vinduer (lik strøm i NL og PL). For et tilfelle med fire AT-vinduer kan en korreksjonsfaktor på anslagsvis ''k<sub>PL</sub>''= 0,6 benyttes. | |||
=== Strøm gjennom autotransformatorene i trafikksimuleringer === | |||
Ut fra det en har sett over angående belastning av autotransformatorene vil de belastes lavt på grunn av den store andelen effektoverføring kun 15 kV-nivå når det er få AT-vinduer på en kort matestrekning. For å finne belastningen for autotransformatorer ved starten av en strekning med en, to eller tre AT-vinduer og jevnt fordelete tog betraktes figurene ovenfor som viser disse situasjonene. For innmating mot den grå boksen som betraktes fås for innmating fra side 1: | |||
::<math> I_{1AT} = \left | k_{AT}\mathbf{I_{1}} \right \vert </math> | |||
og ved 2 | |||
::<math> I_{2AT} = \left | k_{AT}\mathbf{I_{2}} \right \vert </math> | |||
Der en tar hensyn til antall AT-vinduer ved å ta med faktoren ''k<sub>AT</sub>'' som har verdier gitt av tabellen nedenfor. Verdiene i tabellen er hentet fra figurene med tre, to og ét AT-vindu og like mange tog som viser belastningen av autotransformatorene med tog jevnt fordelt på matestrekningen: | |||
{| class="wikitable" style="margin-left:1em; text-align:center" | {| class="wikitable" style="margin-left:1em; text-align:center" | ||
|+ Strøm i | |+ Strøm i autotransformatorer nærmest innmatepunktene (fra 15 til 30 kV) eller overgang mellom BT- og AT-system. | ||
! | ! !! Tre AT-vinduer !! To AT-vinduer !! Ett AT-vindu | ||
|- | |- | ||
| Strøm i | | Strøm i AT (k<sub>AT</sub>) || 1030/1500 → 0,69 || 520/1000 → 0,52 || 0/500 →0,0 | ||
|} | |||
En formel for strømmen som fordeler seg på autotransformatorene midt på strekningen kan settes opp slik: | |||
::<math> I_{midtAT} = k_{midt AT} \left | \mathbf{I_{1}}+\mathbf{I_{2}} \right \vert </math> | |||
Belastningen av hver autotransformator ute på matestrekningen finnes som summen av strømmen inn på matestrekningen dividert på antall autotransformator. Da kan en regne med at autotransformatoren på midten gjennomsnittlig belastes minst med så stor strøm. Verdiene i tabellen nedenfor viser belastningen av autotransformatorene og er hentet fra figurene med tre og to AT-vinduer og like mange tog: | |||
{| class="wikitable" style="margin-left:1em; text-align:center" | |||
|+ Strøm i autotransformatorer ute på matestrekningen (fra 15 til 30 kV). | |||
! !! Tre AT-vinduer !! To AT-vinduer !! Ett AT-vindu | |||
|- | |- | ||
| Strøm i | | Strøm i midt AT (k<sub>midt AT</sub>) || 1030/3000 → 0,3433 || 520/1000 → 0,52 || – | ||
|} | |} | ||
Der ''k<sub>midt AT</sub>'' er korrigeringsfaktoren autotransformatorer på matestrekningen gitt av verdiene i tabellen ovenfor. I et tilfelle med flere enn tre AT-vinduer antas det at korrigeringsfaktoren k<sub>midt AT</sub> kan erstattes slik, der n er antall autotransformatorer: | |||
::<math> I_{midtAT} = \frac{1}{n} \left | \mathbf{I_{1}}+\mathbf{I_{2}} \right \vert </math> | |||
=== Strøm gjennom autotransformatorer tilknytet et topoelt koblingshus === | |||
For strøm gjennom autotransformatorer tilknyttet et topolet samleskinneanlegg (koblingshus), må en finne strømmen som mates ut på 15 kV-nivå til tilstøtende matestrekninger. Om matestrekningene tilknyttet samleskinneanlegget er lange, autotransformatorene plassert med lik avstand og med jevnt fordelt effektuttak, kan en anta lik belastning for alle autotransformatorene. Men om disse forutsetningene ikke er til stede kan bruk av tommelfingerregler gi feil, for eksempel ved at mer effekt enn vanlig omsettes på 15 kV-nivå og belaster autotransformatorene tilknyttet samleskinnen mye. | |||
Om en kan finne strømmen som går inn til samleskinneanleggets forsyningsområde, markert med grå boks i figuren nedenfor, vil den delen som er togstrømmen belaste autotransformatoren tilknyttet samleskinneanlegget slik: | |||
::<math> I_{khAT} = k_{khAT} \left | \mathbf{I_{1}}+\mathbf{I_{2}}+\mathbf{I_{5}} \right \vert </math> | |||
Det grå området kan ha en utstrekning til nærmeste autotransformator i hver retning ut fra koblingshuset, og har betydning for korrigeringsfaktoren ''k<sub>khAT</sub>''. Problemet her er at en ikke har noen sikre beregninger for hvor stor korrigeringsfaktoren egentlig skal være. | |||
[[Fil:Strømmer i forbindelse med koblingshus med AT-system med tilknytning til mange matestrekninger.png|thumb|senter|900px|Problemstillingen med å finne riktig belastning av autotransformatoren tilknyttet samleskinnen til et koblingsanlegg når det er effektflyt både på 15 kV- og 30 kV-nivå gjennom koblingshuset.]] | |||
En annen mulighet er å betrakte hvert AT-vindu som koblingshuset mater ut til individuelt, se figuren nedenfor. Strømmen som belaster autotransformatoren tilknyttet det topolede samleskinneanlegget sies da å være summen av alle strømmene inn til hvert AT-vindu (grå boks), korrigert med en korrigeringsfaktor: | |||
::<math> I_{ATkoblingshus} = \left | k_{AT1} (\mathbf{I_{1-2}}+\mathbf{I_{2-1}}) + k_{AT2} (\mathbf{I_{3-4}}+\mathbf{I_{4-5}}) + k_{AT3} (\mathbf{I_{5-6}}+\mathbf{I_{6-5}})\right \vert </math> | |||
< | Den enkleste måten å håndtere korreksjonsfakterene på er å si at de alle er lik og at halvparten av strømmen for hvert AT-vindu fordeles likt, altså at ''k<sub>AT1</sub>''=''k<sub>AT2</sub>''=''k<sub>AT3</sub>''=0,5. Eventuelt at det gjøres vurderinger for forskjellige korigeringsfaktorer. For eksempel at en har en oppfatning om at togene trekker ekstra stor strøm nært koblingshuset i en av de grå boksene, og at korrigeringsfaktoren dermed økes. | ||
[[Fil:Strømmer i forbindelse med koblingshus med AT-system med flere matestrekninger som betraktes individuelt.png|thumb|senter|900px|Problemstillingen med å finne belastning av autotransformatoren tilknytet topolet samleskinne løses med å summere strømmen til hvert av AT-vinduene.]] | |||
== Oppsummering, diskusjon og konklusjon == | |||
En har her utviklet formler og metodikk for å finne belastning av seriekompoenter (PL og AT) i AT-system på korte matestrekninger med stor trafikk. Med korte matestrekninger forstås her tilfeller hvor det er opptil fem AT-vinduer, altså opptil rundt 50 km mellom matestasjoner. Med stor trafikk menes det at strekningen trafikkeres med tog som har kort togfølgetid, slik at det stort sett er ett eller flere tog i hvert AT-vindu til enhver tid. Formelene som er utledet her gjør bruk av begrepene transitt- og togstrøm og forskjellige korrigeringsfaktorer benyttes. Transittstrøm forårsaker symetrisk belastning av AT-lederne, mens togstrøm leder til større belastning av PL enn NL. | |||
Korrigeringsfaktorene bør benyttes med omhu på lengre matestrekninger der bare en mindre del av strekningen skal analyseres ved dimensjonering av et AT-system. Det kan for ekemspel være at en har BT-system på det meste av strekningen og et AT-system som utgjør noen få AT-vinduer der KL-anlegget fornyes. Problemstillingen kan da dreie seg om dimensjonering av AT-ledere og AT-er. Tabellen for korreksjonsfaktorer for strøm i PL angir at korreksjonsfaktoren skal være''k<sub>PL</sub>''=1,0 eller ''k<sub>PL</sub>''=0,74 for henholdsvis ett eller to AT-vinduer, men det vil sannsynligvis være for stor faktor om matestrekningen totalt sett er lang og AT-vinduene ligger rett ved den ene matestasjonen. Om ''k<sub>PL</sub>''=1,0 indikerer det at det ikke er noe transittstrøm, noe som egentlig bare er tilfelle i AT-vinduet midt på en matestrekning eller om det bare er ett AT-vindu mellom matestasjonene. Om matestrekningen er lang, har BT-system og noen få AT-vinduer ved den ene matestasjonen blir en mer realistiks korreksjonsfaktor ''k<sub>PL</sub>''≈ 0,5. Med andre ord trenger en ikke å benytte metodikken her om matestrekningen totalt tilsvarer rundt fem AT-vinduer (rundt 50 km) eller mer. | |||
Utledningen av formlene er basert på betrakning av linjediagrammer og ikke matematiske utlednigner. Det er mulignes en svakhet av formlene er basert på en slik «intuitiv metode». | |||
For helt spesielle dimensjoneringsproblmer som måtte oppstå ved design av AT-system kan formlene som er benyttet her anvendes. Kontroll av strømflyten med andre regneprogrammer som tar hensyn til alle lederne i AT-system og magnetisk kobling mellom dem, må gjerne brukes i tillegg. | |||
== Appendiks== | == Appendiks== | ||
Når det gjelder strømflyten i et AT-system og belastning av AT-ledere og AT-er, er det kun beregninger utført av Varju i 2005 som gir konkrete tall.<ref name=Obuch> Varju, György: ''EMC STUDY FOR ATPLNL SYSTEM IN NORWAY. Budapest, (November, 2005).</ref> Hans beregninger ble gjort for et tilfelle med en matestrekning der ett tog beveger seg mellom matestasonene. Her er det gjort vurderinger for matestrekninger som bare er henholdsvis 30, 20 og 10 km lange, istedenfor 84 km som Varju forutsatte. Tallene i sort er hentet ut fra beregningen, og det er forutsatt at toget trekker 1000 A. (Mens Varju forutsatte 500 A. Dermed er alle verdiene doblet her). | |||
Det som kompliserer forholdene er at noen av strømmen kommer fra autotransformatorer utenfor AT-vinduet der toget befinner seg. Et annt fenomen er strøm som forlater skinnene og går ut i jordsmonnet. Disse strømmene kan utgjøre opptil noen titals apere, men er sett bort fra her. | |||
=== Strømflyt i AT-system med tre AT-vinduer === | |||
I tilfellet der toget er midt på strekningen som i figuren under, ser en at strømmen er likt fordelt mellom PL og NL i føste og tredje AT-vindu. Det tilsvarer omtrent strømflyten beregnet av Varju for tilfellet der toget er ved km 42. Videre vises strømmens komponenter på 15- og 30 kV-nivå med henholdsvis røde og blå piler, mens sorte tall viser virkelig (resulterende) strøm for NL. Alle autotransformatorene her belastes 500 A på sekundersiden og 250 A på primærsiden. I dette tilfelle skjer all effektoverføring fra spenningskildene på 30 kV-nivå og autotransformatorene rett ved toget omsetter strøm til toget på 15 kV-nivå. Det ville vært tilfelle om impedansen i autotransformatorene var null, men siden det ikke er mulig og matestrekningen heller ikke er spesielt lang, vil noe strøm komme fra tilstøtende spenningskilder på 15 kV-nivå. Denne strømmen er såpass liten, anslagsvis noen få amper, at den sees bort fra her. | |||
Om matestrekningen var lengre og det var mange AT-vinduer, ville autotransformatoren mellom spenningskildene og toget ikke omsatt strøm i det hele tatt (kun magentiseringsstrøm). En kan legge merke til at NL i AT-vinduet på midten ikke fører noen strøm. Det vil være tilfellet når impedansen mellom tog og spenningskilde i hver retning er eksakt lik. I praksis vil det bare skje i et lite øyeblikk når toget er midt på matestrekningen. | |||
[[Fil:Tog i andre AT-vindu ut av tre.png|thumb|senter|900px|Strømflyt i AT-ledere med en last som trekker 1000 A rett ved autotransformatoren midt på matestrekningen. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist.]] | |||
For tilfellet når toget er midt i det første AT-vinduet, benyttes strømflyten fra Varjus beregninger for tilfelle med en last ved km 30,0. En last midt i AT-vinduet til høyre vil gi samme strømfordeling. | |||
[[Fil:Tog midt mellom første og andre AT på strekning med tre AT-vinduer.png|thumb|senter|900px|Strømflyt i AT-ledere med en last som trekker 1000 A midt mellom autotransformator nummer én og to på matestrekningen. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist.]] | |||
=== Strømflyt i AT-system med to AT-vinduer === | |||
Figuren nedenfor viser strømmen som flyter i lederne i et AT-system med to AT-vinduer basert på beregningene utført av Varju, samt antagelser for en matestrekning som er 20 km lang istedenfor 84 km. Ellers samme forutsetninger og symboler som over. Det forventes at på en så kort strekning som dette vil begge spenningskildene bidra nokså mye, anslagsvis med fordelingen ⅔ og ⅓ fra spenningskildene henholdsvis til venstre og høyre. Beregningene fra Varju benyttes for toget plassert ved km 30,0. Som en ser, kommer det vesentlige av strømmen via PL fra den nærmeste spenningskilden for denne posisjonen av lasten: | |||
[[Fil:Tog midt mellom første og andre AT på strekning med to AT-vinduer.png|thumb|senter|900px|Strømflyt i AT-ledere med en last som trekker 1000 A mellom autotransformatorene på første AT-vindu på matestrekningen. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist.]] | |||
=== Strømflyt i AT-system med ett AT-vindu === | |||
I figurene nedenfor er det vist strømfordelingen for en matestrekning bestående kun av ett AT-vindu. Strømmene (sorte tall) er hentet ut fra tilfellet der toget er ved km 42,000, altså midt i AT-vinduet som ligger midt ut på matestrekingen i beregningen til Varju. Det er (tilnærmet) ingen strøm som går i NL og all strøm overføres på 15 kV-nivå i PL. | |||
[[Fil:Tog midt på strekning med ett AT-vindu.png|thumb|senter|900px|Strømflyt i AT-ledere med en last som trekker 1000 A rett ved autotransformatoren midt på matestrekningen. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå.]] | |||
== Referanser == | == Referanser == | ||
Siste sideversjon per 24. mai 2024 kl. 07:05
Innledning
Beregning av strømflyt, termisk belastning og dimensjonering av seriekomponenter i autotransformatorsystem (AT-system) med svært stor belastning og kort matestrekning kan være utfordrende, fordi strømflyten i AT-lederne ikke er symetrisk. For eksempel vil det på en jernbanestrekningmed AT-system (elektrisk utforming E) og stor togtrafikk gå mer strøm i positivleder (PL) enn i negativleder (NL). Om en har elektrisk utforming F vil det på samme måte gå mer størm i kontaktledningen (KL). Artikkelen her fokuserer på elektrisk utforming E, samt formler for å finne strømbelastningen i autotransformatorer (AT) og positivleder (PL).
Med stor togtrafikk menes at det på en matestrekning går så mange tog at det for det meste av tiden vil være ett eller flere tog mellom hver AT, eller AT-vindu. Da vil det være mye strøm som overføres enfaset (eller 15 kV-nivå) og mindre tofaset (eller på 30 kV-nivå). Desto større trafikk desto større blir denne tendensen. Motsatt vil større effekt i transitt, altså effekt som overføres fra en matestrekning til en annen eller forbi ett eller flere AT-vinduer, medføre lik strøm i PL og NL. Det vil være det samme som å si at det overføres effekt tofaset.
Det som også kompliserer forholdene er stor effekt i transitt, altså effekt som overføres mellom matestrekninger og forbi koblingshus og matestasjoner. Metoden som det her bygges på forutsetter at det foreligger en trafikksimulering der aktiv og reaktiv effekt, samt spenning, er kjent for innmatepunktene til strekningen som skal analyseres. Disse størrelsen brukes til å finne strømmenes fasevektorer (komplekse størrelser). Det fokuseres dessuten på korte strekninger (kort avstand mellom matestasjoner). Først og fremst vil det være en problmestilling i Oslo-området fordi det her er stor trafikk og bare noen få mil mellom omformerstasjonene.
Første del av artikkelen handler om strømflyten i AT-system med få AT-vinduer. Dette brukes for å finne spesielle korreksjonsfaktorer. Deretter utledes formler for å beregne strømflyt. Med å kombinere verdier fra simuleringer med formlene som utledes her, kan en fine strøm som funksjon av tid i AT-ledere og AT-er. Ved hjelp av termiske modeller kan en deretter finne temperatur som funksjon av tiden, noe som vil være nyttig ved dimensjonering av autotransformatorer, aluminiumsliner og kraftkabler.
Strømflyt i AT-system på kort matestrekning med tog i alle AT-vinduer
I appendiks er det vist strømfordeling med last i bare ett AT-vindu for matestrekning med en, to og tre AT-vinduer. Her blir det vist strømfordeling med så stor trafikk at det til enhver tid er tog i alle AT-vinduene.
Strømflyt i AT-system med tre AT-vinduer
For å finne strømmen som flyter i AT-lederne på en matestrekning med tre AT-vinduer undersøkes figuren under og en metodikk basert på superposisjonsteoremet. Først hentes det ut figurer for togplassering og strøm midt i hvert AT-vindu fra appendiks. Togene byttes ut med strømkilder som trekker strøm tilsvarende togene. Summen av strømmene til de tre lastene finnes av superposisjonsteoremet som sier at: Den totale strømmen i en hvilken som helst del av en lineær krets tilsvarer den algebraiske summen av strømmer gitt av strømkilde hver for seg. For å bestemme summen av separate strømmer, erstattes alle andre spenningskilder med en kortslutning og alle andre strømkilder med åpne kretser. Dermed fås summen som er vist i det nederste linjediagrammet. Som en kan se er strømfordelingen for AT-lederne ved spenningskildene 66 % i PL og 34 % i NL.
Strømflyt i AT-system med to AT-vinduer
For anslag av strømfordelingen med last midt på hvert av AT-vinduene, tas det utgangspunkt i tilfellet med én last midt mellom AT-en på en strekning med to AT-vinduer (se appendiks). Det forventes at på en så kort strekning som dette vil begge spenningskildene bidra nokså mye, anslagsvis med fordelingen ⅔ og ⅓ fra spenningskildene henholdsvis til venstre og høyre. I det nederste linjediagrammet er strømmene summert algebraisk. Strømfordelingen for AT-lederne ved spenningskildene er 74 % i PL og 26 % i NL.
Strømflyt i AT-system med ett AT-vindu
I figuren er det vsit strømfordelingen for en matestrekning bestående kun av ett AT-vindu, se appendiks for forklaring. Strømfordelingen for AT-lederne ved spenningskildene er 100 % i PL og 0 % i NL.
Tabellen under er en oppsummering av undersøkelsene her og viser usymmetrisk belastning av AT-ledere med en matestrekning bestående av ett, to eller tre AT-vinduer:
| Leder | Tre AT-vinduer | To AT-vinduer | Ett AT-vindu |
|---|---|---|---|
| Strøm i NL | 515/1500 → 0,34 | 260/1000 → 0,26 | 0/500 →0,0 |
| Strøm i PL | 985/1500 → 0,66 | 740/1000 → 0,74 | 500/500 →1,0 |
Tabellen viser en interessant tendens, nemmlig at strømmen i NL og PL blir stadige mer jevnt fordelt med økende antall AT-vinduer. Med anslagsvis fem eller flere AT-vinduer ville sannsynligvis strømfordelingen blitt lik mellom de to lederne.
Beregning av strøm i AT-ledere og autotransformatorer i trafikksimuleringer
For tog som trekker 1000 A og beveger seg mellom to spenningskilder på en matestrekning med tre, to eller ett AT-vindu, vil strømmen altså fordele seg nokså ulikt mellom AT-lederne. Dette i motsetning til en matestrekning med mange AT-vinduer der strømmen blir jevn. Tre ting gjør at representasjonen i kapitlet over er en sterk forenkling:
- Spenningskildene er ingen realistisk representasjon av virkelige omformerstasjoner. I virkeligheten vil blant annet antall omformere i drift, indre impedans og spenningsregulatorer spiller inn.
- Togene trekke stor strøm visse steder (hastighetsøkning), mens de andre steder trekker de moderat (jevn hastighet, liten stigning og rulling), ingen strøm (rulling med liten fall) eller mater inn strøm (regenerativ bremsing i fall).
- Strømfordeling for effekt i transitt er ikke undersøkt, men en del effekt vil overføres på en matestrekning til den neste. Denne effekten fordeler seg likt mellom AT-lederne.
For de aktuelle strekningene som en ser på her vil det være stasjoner ved hver av autotransformatorene. Togene kjører ut av stasjonene og akselererer opp i hastighet rett utenfor stasjonene. Det kan derfor godt tenkes stort strømforbruk før togene kommer midt mellom autotransformatorene. Effektfordeling mellom omformerstasjonene som har sammenheng med første kulepunkt blir inkludert i modellene for trafikksimuleringene og vil være gitt i resultatene.
For en sinusformet strøm eller spenning gjelder helt grunnlegende disse funksjonene med hensyn på tiden:
der
- = momentanverdien av strømmen i tidspunktet t [A]
- = momentanverdien spenningen i tidspunktet t [V]
- = maksimumsverdi for strømmen, også kalt amplitude [A]
- = maksimumsverdi for spenningen, også kalt amplitude [V]
- = vinkelfrekvens i radianer [s-1]
- = tiden [s]
- = fasevinkel, faseforskyvning [rad]
Videre i teksten benyttes det viserstørrelser (fasevektor) med uthevede bokstaver, der selve definisjonen er slik:
i tillegg til de symbolene som er definert over har en:
- er symbolet for fasevektortransformasjonen
- e = grunntallet for den naturlige logaritmen
- j = den imaginære enheten ()
- I = strømmen som viserstrørrelse
En sier at fasevektortransformasjonen overfører sinusfunksjonen for strøm eller spenning (til høyre i parantes i formelen over) fra tidsplanet til kompleksplanet. I denne transformasjonen fjernes informasjonen om frekvens og tid. Formen over er på polar form, men kartesisk form er like vanlig, da får uttrykket over denne formen:
I elektroteknikken innføres notasjonen som er enklere å skrive når en bruker polar form.
Strøm i AT-ledere trafikksimuleringer
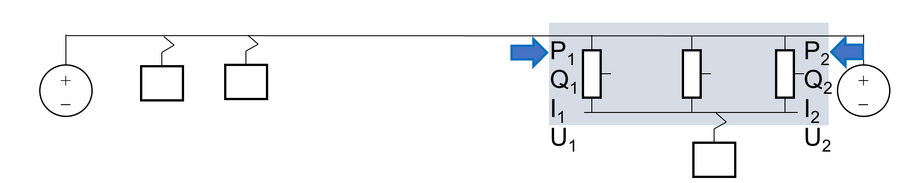
En skal her utlede formler og sette opp en metodikk for belastning av AT-ledere på en strekning vist med en grå boks i hver av illustrasjonene nedenfor. Generelt betraktes en kort matestrekning mellom to omformerstasjoner, som i det øverste bilde nedenfor. Problemstillingen kan også være et strekningsavsnitt med delvis AT-system og BT-system, se det nederste bildet.
Det vil for hver av disse grå boksene kunne være en strøm- og effektkomponent som går rett gjennom, her kalt transittstrøm. En annen del går inn i boksen og brukes av togene, kalt togstrøm. De blå pilene viser fortegnkonvensjonen som benyttes, slik at strøm og effekt inn til boksen er togstrøm.
Transittstrømmen som altså går forbi det grå feltet fra venstre mot høyre i figurene er gitt av sammenhengen:
og fra høyre mot venstre i figurene:
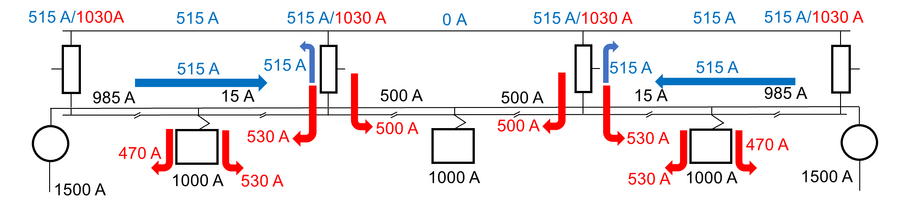
med positive verdier i pilenes retning i figuren og strømmer referert til 15 kV-nivå. En multipliserer med ½ for å ta hensyn til at strømmen (I1 og I2) halveres på grunn av doblet spenningsnivå inn i boksene. Grunnen til at en må ta differansen av strømmen I1 og I2 når en ønsker å finne I1-2PLT og I1-2NLT gjennom den grå boksen fra 1 til 2, er at noe av strømmen forbrukes av togene inn i boksen. Det samme gjelder for I2-1PLT og I2-1NLT. En kan betrakte figuren nedenfor med tre tog for å forsikre seg om at det stemmer. Sammenhengen må gjelde både for en matestrekning, flere AT-vinduer etter hverandre og kun ett AT-vindu. I AT-vinduet til høyre går det inn en strøm på 1500 A fra spenningskilden og ut av AT-vinduet går det en strøm på 500 A (rød pil ved tredje AT), dermed fås 1500–500 = 1000 A, som ved å deles på 2 blir strømmen på 30 kV-nivå (tofaset strøm), altså 500 A. I figuren er det 515 A (blå tall) i NL og PL i det høyre AT-vinduet som overføres på 30 kV-nivå, men noe av denne strømmen blir overført til toget i dette AT-vinduet. Denne delen på 15 A er altså ikke transittstrøm.
Strømmen som tog komsumerer på strekningen innenfor den grå boksen er gitt av:
og strømmen i PL som tog komsumerer:
Der en multipliserer med ½ for at summen av strøm inn på AT-vinduet fordeles på lederne fra hver retning frem til toget. I tillegg må korrigeringsfaktoren kPL anvendes for å ta hensyn til asymmetrisk strømfordeling med få AT-vinduer. Her kan en igjen benytte figuren under for å forsikre seg om at formelene stemmer. Summen av strømmene inn til AT-vinduet til høyre er 1500+500 = 2000 A, som ved å deles på 2 blir 1000 A. Altså den strømmen som toget trekker og som går i PL fra hver retning. Strømmen i PL fra høyre er 985 A. Korreksjonsfaktoren kPL skal altså benyttes for å justere resultatet for å ta hensyn til ujevn strømfordeling mellom AT-lederne ved få AT-vinduer.
Fra simuleringsprogrammene μPAS eller TPSS kan en kun få verdiene for aktiv- og reaktiv effekt i en seriekomponent (med fortegn), samt spenning og strøm. Imidlertid får en ikke strømmene oppgitt som fasevisere. Alle verdiene som fås fra μPAS eller TPSS vil dessuten være referert 15 kV-nivå. For å finne strømmene I1 og I2 benyttes sammenhengen:
Her defineres fasevinkelen til spenningen som referanse og settes til 0°. Det innebærer at fasevinkelforskjellen for spenningen over denne korte strekningen tilnærmes til å være 0°. Videre kan en finne strømmene I1 og I2 når effekt og spenning er kjent fra simuleringer:
Dermed kan en finne strømmen som går i PL ved 1 i de grå boksene i skissene over ved å sette inn for summen av togstrøm (IPLtog) og transittstrøm (IPLT):
og ved 2:
Her er det første leddet (differansen) strømkomponenten som overføres forbi AT-vinduet(ene), altså transittstrøm, og det andre leddet er strøm som togene på strekningen forbruker, altså togstrøm.
Korreksjonsfaktorene for hver av situasjonene med tre, to og ett AT-vindu finnes ved å settes inn alle størrelsene i uttrykkene over og løse disse ut som ligninger. For situasjonen med tre tog i midten av tre AT-vinduer gir dette: ¼·(1500–1500)+½·kPL·(1500+1500) = 985, som gir kPL = 0,66. For tilfellet med to tog og to AT-vinduer fås kPL = 0,74 og for ett tog og AT-vindu kPL = 1,0. Dette er de samme tallene som en satte opp i tabellen over som viste usymetrisk belastning mellom NL og PL. Tabellen gjentas her:
| Tre AT-vinduer | To AT-vinduer | Ett AT-vindu | |
|---|---|---|---|
| kPL | 0,66 | 0,74 | 1,0 |
Korreksjonsfaktoren vil som tidligere nevnt gå mot 0,5 om det er anslagsvis fem AT-vinduer (lik strøm i NL og PL). For et tilfelle med fire AT-vinduer kan en korreksjonsfaktor på anslagsvis kPL= 0,6 benyttes.
Strøm gjennom autotransformatorene i trafikksimuleringer
Ut fra det en har sett over angående belastning av autotransformatorene vil de belastes lavt på grunn av den store andelen effektoverføring kun 15 kV-nivå når det er få AT-vinduer på en kort matestrekning. For å finne belastningen for autotransformatorer ved starten av en strekning med en, to eller tre AT-vinduer og jevnt fordelete tog betraktes figurene ovenfor som viser disse situasjonene. For innmating mot den grå boksen som betraktes fås for innmating fra side 1:
og ved 2
Der en tar hensyn til antall AT-vinduer ved å ta med faktoren kAT som har verdier gitt av tabellen nedenfor. Verdiene i tabellen er hentet fra figurene med tre, to og ét AT-vindu og like mange tog som viser belastningen av autotransformatorene med tog jevnt fordelt på matestrekningen:
| Tre AT-vinduer | To AT-vinduer | Ett AT-vindu | |
|---|---|---|---|
| Strøm i AT (kAT) | 1030/1500 → 0,69 | 520/1000 → 0,52 | 0/500 →0,0 |
En formel for strømmen som fordeler seg på autotransformatorene midt på strekningen kan settes opp slik:
Belastningen av hver autotransformator ute på matestrekningen finnes som summen av strømmen inn på matestrekningen dividert på antall autotransformator. Da kan en regne med at autotransformatoren på midten gjennomsnittlig belastes minst med så stor strøm. Verdiene i tabellen nedenfor viser belastningen av autotransformatorene og er hentet fra figurene med tre og to AT-vinduer og like mange tog:
| Tre AT-vinduer | To AT-vinduer | Ett AT-vindu | |
|---|---|---|---|
| Strøm i midt AT (kmidt AT) | 1030/3000 → 0,3433 | 520/1000 → 0,52 | – |
Der kmidt AT er korrigeringsfaktoren autotransformatorer på matestrekningen gitt av verdiene i tabellen ovenfor. I et tilfelle med flere enn tre AT-vinduer antas det at korrigeringsfaktoren kmidt AT kan erstattes slik, der n er antall autotransformatorer:
Strøm gjennom autotransformatorer tilknytet et topoelt koblingshus
For strøm gjennom autotransformatorer tilknyttet et topolet samleskinneanlegg (koblingshus), må en finne strømmen som mates ut på 15 kV-nivå til tilstøtende matestrekninger. Om matestrekningene tilknyttet samleskinneanlegget er lange, autotransformatorene plassert med lik avstand og med jevnt fordelt effektuttak, kan en anta lik belastning for alle autotransformatorene. Men om disse forutsetningene ikke er til stede kan bruk av tommelfingerregler gi feil, for eksempel ved at mer effekt enn vanlig omsettes på 15 kV-nivå og belaster autotransformatorene tilknyttet samleskinnen mye.
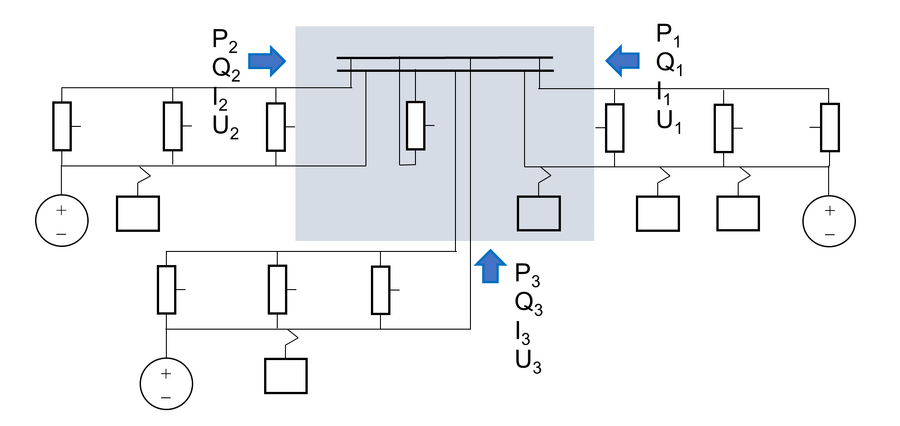
Om en kan finne strømmen som går inn til samleskinneanleggets forsyningsområde, markert med grå boks i figuren nedenfor, vil den delen som er togstrømmen belaste autotransformatoren tilknyttet samleskinneanlegget slik:
Det grå området kan ha en utstrekning til nærmeste autotransformator i hver retning ut fra koblingshuset, og har betydning for korrigeringsfaktoren kkhAT. Problemet her er at en ikke har noen sikre beregninger for hvor stor korrigeringsfaktoren egentlig skal være.
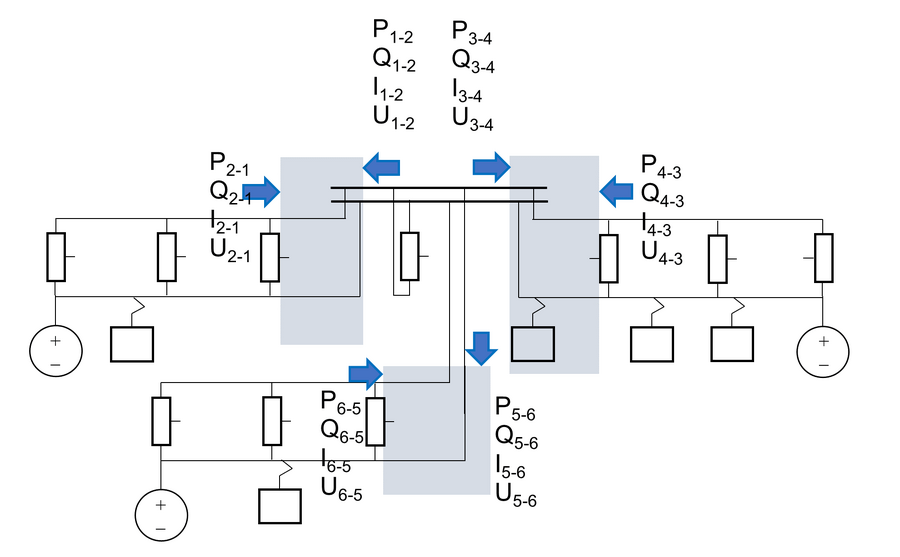
En annen mulighet er å betrakte hvert AT-vindu som koblingshuset mater ut til individuelt, se figuren nedenfor. Strømmen som belaster autotransformatoren tilknyttet det topolede samleskinneanlegget sies da å være summen av alle strømmene inn til hvert AT-vindu (grå boks), korrigert med en korrigeringsfaktor:
Den enkleste måten å håndtere korreksjonsfakterene på er å si at de alle er lik og at halvparten av strømmen for hvert AT-vindu fordeles likt, altså at kAT1=kAT2=kAT3=0,5. Eventuelt at det gjøres vurderinger for forskjellige korigeringsfaktorer. For eksempel at en har en oppfatning om at togene trekker ekstra stor strøm nært koblingshuset i en av de grå boksene, og at korrigeringsfaktoren dermed økes.
Oppsummering, diskusjon og konklusjon
En har her utviklet formler og metodikk for å finne belastning av seriekompoenter (PL og AT) i AT-system på korte matestrekninger med stor trafikk. Med korte matestrekninger forstås her tilfeller hvor det er opptil fem AT-vinduer, altså opptil rundt 50 km mellom matestasjoner. Med stor trafikk menes det at strekningen trafikkeres med tog som har kort togfølgetid, slik at det stort sett er ett eller flere tog i hvert AT-vindu til enhver tid. Formelene som er utledet her gjør bruk av begrepene transitt- og togstrøm og forskjellige korrigeringsfaktorer benyttes. Transittstrøm forårsaker symetrisk belastning av AT-lederne, mens togstrøm leder til større belastning av PL enn NL.
Korrigeringsfaktorene bør benyttes med omhu på lengre matestrekninger der bare en mindre del av strekningen skal analyseres ved dimensjonering av et AT-system. Det kan for ekemspel være at en har BT-system på det meste av strekningen og et AT-system som utgjør noen få AT-vinduer der KL-anlegget fornyes. Problemstillingen kan da dreie seg om dimensjonering av AT-ledere og AT-er. Tabellen for korreksjonsfaktorer for strøm i PL angir at korreksjonsfaktoren skal værekPL=1,0 eller kPL=0,74 for henholdsvis ett eller to AT-vinduer, men det vil sannsynligvis være for stor faktor om matestrekningen totalt sett er lang og AT-vinduene ligger rett ved den ene matestasjonen. Om kPL=1,0 indikerer det at det ikke er noe transittstrøm, noe som egentlig bare er tilfelle i AT-vinduet midt på en matestrekning eller om det bare er ett AT-vindu mellom matestasjonene. Om matestrekningen er lang, har BT-system og noen få AT-vinduer ved den ene matestasjonen blir en mer realistiks korreksjonsfaktor kPL≈ 0,5. Med andre ord trenger en ikke å benytte metodikken her om matestrekningen totalt tilsvarer rundt fem AT-vinduer (rundt 50 km) eller mer.
Utledningen av formlene er basert på betrakning av linjediagrammer og ikke matematiske utlednigner. Det er mulignes en svakhet av formlene er basert på en slik «intuitiv metode».
For helt spesielle dimensjoneringsproblmer som måtte oppstå ved design av AT-system kan formlene som er benyttet her anvendes. Kontroll av strømflyten med andre regneprogrammer som tar hensyn til alle lederne i AT-system og magnetisk kobling mellom dem, må gjerne brukes i tillegg.
Appendiks
Når det gjelder strømflyten i et AT-system og belastning av AT-ledere og AT-er, er det kun beregninger utført av Varju i 2005 som gir konkrete tall.[1] Hans beregninger ble gjort for et tilfelle med en matestrekning der ett tog beveger seg mellom matestasonene. Her er det gjort vurderinger for matestrekninger som bare er henholdsvis 30, 20 og 10 km lange, istedenfor 84 km som Varju forutsatte. Tallene i sort er hentet ut fra beregningen, og det er forutsatt at toget trekker 1000 A. (Mens Varju forutsatte 500 A. Dermed er alle verdiene doblet her).
Det som kompliserer forholdene er at noen av strømmen kommer fra autotransformatorer utenfor AT-vinduet der toget befinner seg. Et annt fenomen er strøm som forlater skinnene og går ut i jordsmonnet. Disse strømmene kan utgjøre opptil noen titals apere, men er sett bort fra her.
Strømflyt i AT-system med tre AT-vinduer
I tilfellet der toget er midt på strekningen som i figuren under, ser en at strømmen er likt fordelt mellom PL og NL i føste og tredje AT-vindu. Det tilsvarer omtrent strømflyten beregnet av Varju for tilfellet der toget er ved km 42. Videre vises strømmens komponenter på 15- og 30 kV-nivå med henholdsvis røde og blå piler, mens sorte tall viser virkelig (resulterende) strøm for NL. Alle autotransformatorene her belastes 500 A på sekundersiden og 250 A på primærsiden. I dette tilfelle skjer all effektoverføring fra spenningskildene på 30 kV-nivå og autotransformatorene rett ved toget omsetter strøm til toget på 15 kV-nivå. Det ville vært tilfelle om impedansen i autotransformatorene var null, men siden det ikke er mulig og matestrekningen heller ikke er spesielt lang, vil noe strøm komme fra tilstøtende spenningskilder på 15 kV-nivå. Denne strømmen er såpass liten, anslagsvis noen få amper, at den sees bort fra her.
Om matestrekningen var lengre og det var mange AT-vinduer, ville autotransformatoren mellom spenningskildene og toget ikke omsatt strøm i det hele tatt (kun magentiseringsstrøm). En kan legge merke til at NL i AT-vinduet på midten ikke fører noen strøm. Det vil være tilfellet når impedansen mellom tog og spenningskilde i hver retning er eksakt lik. I praksis vil det bare skje i et lite øyeblikk når toget er midt på matestrekningen.
For tilfellet når toget er midt i det første AT-vinduet, benyttes strømflyten fra Varjus beregninger for tilfelle med en last ved km 30,0. En last midt i AT-vinduet til høyre vil gi samme strømfordeling.
Strømflyt i AT-system med to AT-vinduer
Figuren nedenfor viser strømmen som flyter i lederne i et AT-system med to AT-vinduer basert på beregningene utført av Varju, samt antagelser for en matestrekning som er 20 km lang istedenfor 84 km. Ellers samme forutsetninger og symboler som over. Det forventes at på en så kort strekning som dette vil begge spenningskildene bidra nokså mye, anslagsvis med fordelingen ⅔ og ⅓ fra spenningskildene henholdsvis til venstre og høyre. Beregningene fra Varju benyttes for toget plassert ved km 30,0. Som en ser, kommer det vesentlige av strømmen via PL fra den nærmeste spenningskilden for denne posisjonen av lasten:
Strømflyt i AT-system med ett AT-vindu
I figurene nedenfor er det vist strømfordelingen for en matestrekning bestående kun av ett AT-vindu. Strømmene (sorte tall) er hentet ut fra tilfellet der toget er ved km 42,000, altså midt i AT-vinduet som ligger midt ut på matestrekingen i beregningen til Varju. Det er (tilnærmet) ingen strøm som går i NL og all strøm overføres på 15 kV-nivå i PL.
Referanser
- ↑ Varju, György: EMC STUDY FOR ATPLNL SYSTEM IN NORWAY. Budapest, (November, 2005).